六年级上册数学单元检测-《数与形》人教版(含答案)
文档属性
| 名称 | 六年级上册数学单元检测-《数与形》人教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 102.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-22 00:00:00 | ||
图片预览

文档简介
《数与形》单元检测(1)
一、填空题。(第5题14分,其余每空2分,共32分)
1. 按规律填数。
(1),,,,( )。
(2)1,9,25,49,( ),( ),169。
2. 如下图,用同样的小棒摆正方形,像这样摆10个同样的正方形需要小棒( )根;用100根小棒可以摆( )个这样的正方形。
3. 已知121=112,12321=1112,1234321=11112 ,…,那么12345678987654321=( )。
4.
(1)将表格补充完整。
(2)根据表中规律,八边形的内角和是( )。
(3)假设图形的边数为a(a≥3),内角和是S,请你用一个含有字母的关系式表示图形边数与内角和的关系:S=( )。
5.仿照例子,画图计算。
+=1-=
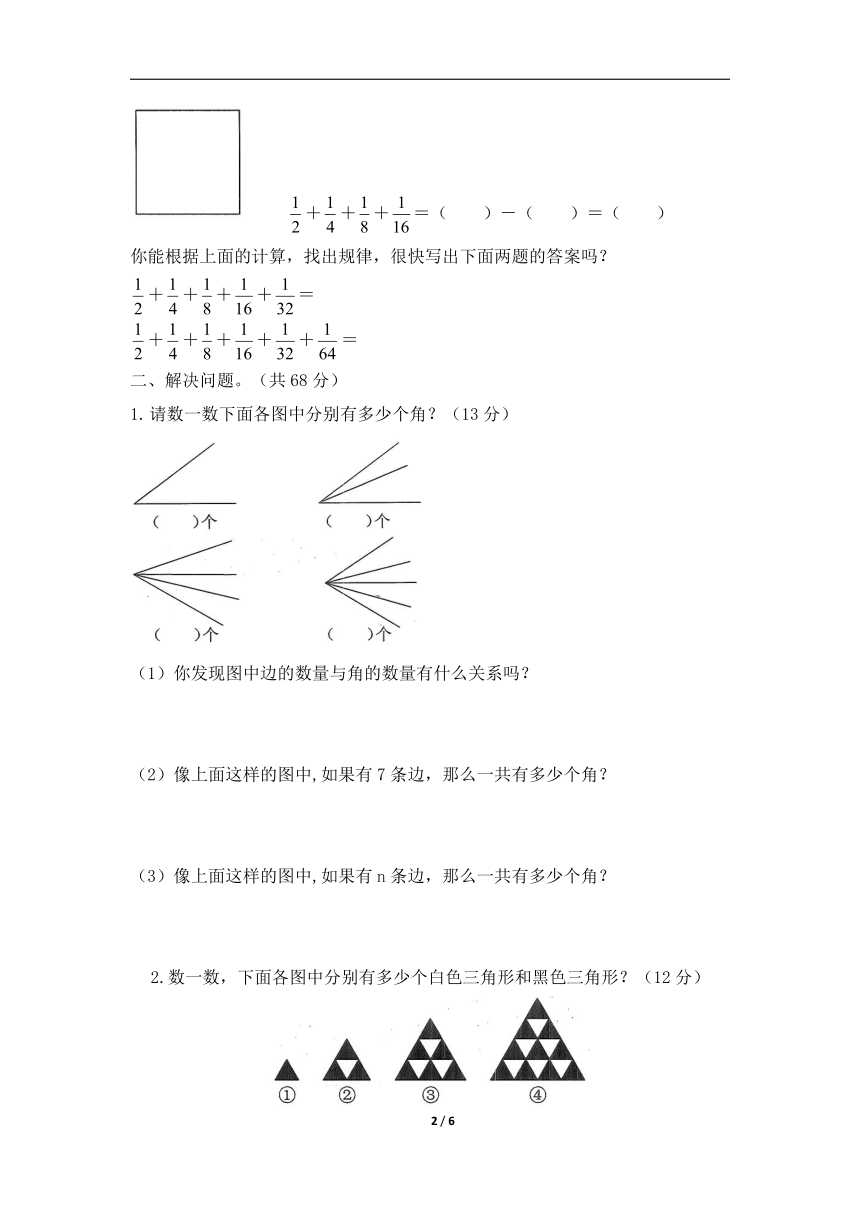
++=( )-( )=( )
+++=( )-( )=( )
你能根据上面的计算,找出规律,很快写出下面两题的答案吗?
++++=
+++++=
二、解决问题。(共68分)
1. 请数一数下面各图中分别有多少个角?(13分)
(1)你发现图中边的数量与角的数量有什么关系吗?
(2)像上面这样的图中,如果有7条边,那么一共有多少个角?
(3)像上面这样的图中,如果有n条边,那么一共有多少个角?
2.数一数,下面各图中分别有多少个白色三角形和黑色三角形?(12分)
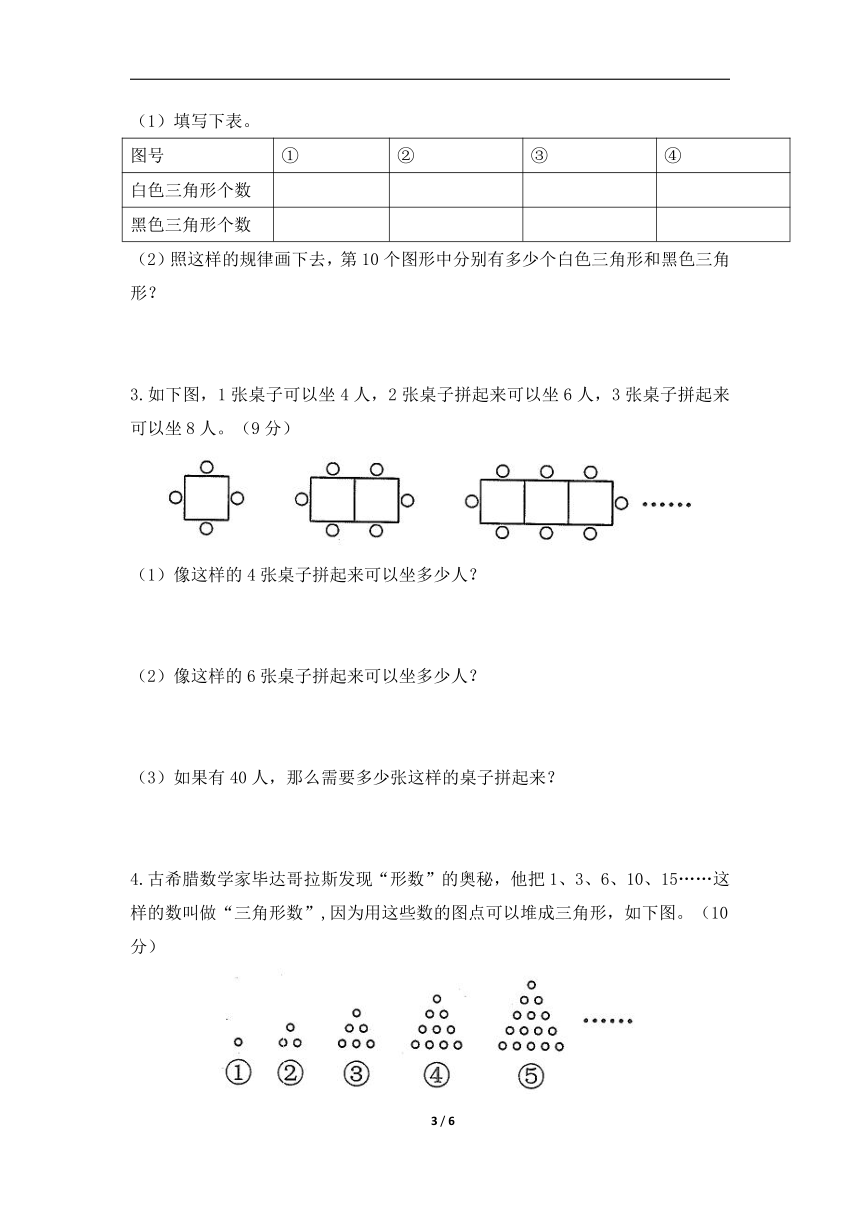
(1)填写下表。
图号
①
②
③
④
白色三角形个数
黑色三角形个数
(2)照这样的规律画下去,第10个图形中分别有多少个白色三角形和黑色三角形?
3.如下图,1张桌子可以坐4人,2张桌子拼起来可以坐6人,3张桌子拼起来可以坐8人。(9分)
(1)像这样的4张桌子拼起来可以坐多少人?
(2)像这样的6张桌子拼起来可以坐多少人?
(3)如果有40人,那么需要多少张这样的桌子拼起来?
4.古希腊数学家毕达哥拉斯发现“形数”的奥秘,他把1、3、6、10、15……这样的数叫做“三角形数”,因为用这些数的图点可以堆成三角形,如下图。(10分)
仔细观察:
图①:1=1
图②:3=1+2
图③:6=1+2+3
图④:10=( )+( )+( )+( )
图⑤:( )=( )+( )+( )+( )+( )
……
你发现了什么规律?按这样的规律排下去,第 10个三角形中有多少个点?第20个呢?
5. 学校的教学楼有四层。六年级一班的学生第一节课到二楼上数学课,第二节课到三楼上美术课,第三节课到二楼上语文课,第四节课到四楼上音乐课,中午到一楼食堂吃饭。下面图( )描述的是六年级一班学生的这一活动过程。 (8分)
6. 甲、乙、丙、丁与小明五人进人象棋比赛的决赛,每两人要比赛一场,每胜一场得2分,和一场得1分,输一场得0分。到现在为止,甲赛了4场,得2分;乙赛了3场,得4分;丙赛了2场,得1分;丁赛了1场,得2分。那么小明现在已经赛了几场?得多少分? (8分)
7. 张林带着他心爱的小狗去外婆家。他步行的速度是每分钟80米,小狗以每分钟200米的速度奔向了外婆家。小狗过了8分钟到达外婆家后又立刻返回,路上遇见张林后它又返回奔向外婆家…… 就这样它不停来回跑。当张林到达外婆家时,小狗总共跑了多少米?(8分)
《数与形》单元检测(1)参考答案
一、1. (1) (2) 81 121
2. 31 33
3. lllllllll2
4.(1) 180°×4 (2) 180°×6 (3) 180°×(a-2)
5.画图略 1 1
二、1. 1 3 6 10
(1) 1+2+3+…+(边的数量-1)=角的数量
(2) 1+2+3+…+6=21(个)
(3) [1+2+3+…+(n-1)]个
2.(1)从上往下,从左往右依次填:0 1 1 3 36 6 10
(2)白色三角形:l+2+3+…+9=45(个)
黑色三角形:1+2+3+…+10=55(个)
3.(1)4×2+2=10(人)
(2)6×2+2=14(人)
(3)(40-2)÷2=19(张)
4. 1 2 3 4 15 1 2 3 4 5
规律:第n个三角形中点的个数就是从1加到n 55个 210个
5.③
6.赛了2场 得3分
7. 200×8÷80×200=4000(米)
一、填空题。(第5题14分,其余每空2分,共32分)
1. 按规律填数。
(1),,,,( )。
(2)1,9,25,49,( ),( ),169。
2. 如下图,用同样的小棒摆正方形,像这样摆10个同样的正方形需要小棒( )根;用100根小棒可以摆( )个这样的正方形。
3. 已知121=112,12321=1112,1234321=11112 ,…,那么12345678987654321=( )。
4.
(1)将表格补充完整。
(2)根据表中规律,八边形的内角和是( )。
(3)假设图形的边数为a(a≥3),内角和是S,请你用一个含有字母的关系式表示图形边数与内角和的关系:S=( )。
5.仿照例子,画图计算。
+=1-=
++=( )-( )=( )
+++=( )-( )=( )
你能根据上面的计算,找出规律,很快写出下面两题的答案吗?
++++=
+++++=
二、解决问题。(共68分)
1. 请数一数下面各图中分别有多少个角?(13分)
(1)你发现图中边的数量与角的数量有什么关系吗?
(2)像上面这样的图中,如果有7条边,那么一共有多少个角?
(3)像上面这样的图中,如果有n条边,那么一共有多少个角?
2.数一数,下面各图中分别有多少个白色三角形和黑色三角形?(12分)
(1)填写下表。
图号
①
②
③
④
白色三角形个数
黑色三角形个数
(2)照这样的规律画下去,第10个图形中分别有多少个白色三角形和黑色三角形?
3.如下图,1张桌子可以坐4人,2张桌子拼起来可以坐6人,3张桌子拼起来可以坐8人。(9分)
(1)像这样的4张桌子拼起来可以坐多少人?
(2)像这样的6张桌子拼起来可以坐多少人?
(3)如果有40人,那么需要多少张这样的桌子拼起来?
4.古希腊数学家毕达哥拉斯发现“形数”的奥秘,他把1、3、6、10、15……这样的数叫做“三角形数”,因为用这些数的图点可以堆成三角形,如下图。(10分)
仔细观察:
图①:1=1
图②:3=1+2
图③:6=1+2+3
图④:10=( )+( )+( )+( )
图⑤:( )=( )+( )+( )+( )+( )
……
你发现了什么规律?按这样的规律排下去,第 10个三角形中有多少个点?第20个呢?
5. 学校的教学楼有四层。六年级一班的学生第一节课到二楼上数学课,第二节课到三楼上美术课,第三节课到二楼上语文课,第四节课到四楼上音乐课,中午到一楼食堂吃饭。下面图( )描述的是六年级一班学生的这一活动过程。 (8分)
6. 甲、乙、丙、丁与小明五人进人象棋比赛的决赛,每两人要比赛一场,每胜一场得2分,和一场得1分,输一场得0分。到现在为止,甲赛了4场,得2分;乙赛了3场,得4分;丙赛了2场,得1分;丁赛了1场,得2分。那么小明现在已经赛了几场?得多少分? (8分)
7. 张林带着他心爱的小狗去外婆家。他步行的速度是每分钟80米,小狗以每分钟200米的速度奔向了外婆家。小狗过了8分钟到达外婆家后又立刻返回,路上遇见张林后它又返回奔向外婆家…… 就这样它不停来回跑。当张林到达外婆家时,小狗总共跑了多少米?(8分)
《数与形》单元检测(1)参考答案
一、1. (1) (2) 81 121
2. 31 33
3. lllllllll2
4.(1) 180°×4 (2) 180°×6 (3) 180°×(a-2)
5.画图略 1 1
二、1. 1 3 6 10
(1) 1+2+3+…+(边的数量-1)=角的数量
(2) 1+2+3+…+6=21(个)
(3) [1+2+3+…+(n-1)]个
2.(1)从上往下,从左往右依次填:0 1 1 3 36 6 10
(2)白色三角形:l+2+3+…+9=45(个)
黑色三角形:1+2+3+…+10=55(个)
3.(1)4×2+2=10(人)
(2)6×2+2=14(人)
(3)(40-2)÷2=19(张)
4. 1 2 3 4 15 1 2 3 4 5
规律:第n个三角形中点的个数就是从1加到n 55个 210个
5.③
6.赛了2场 得3分
7. 200×8÷80×200=4000(米)
