人教版数学四年级上册第一单元《亿以上的数的改写和求近似数》教案(表格版)
文档属性
| 名称 | 人教版数学四年级上册第一单元《亿以上的数的改写和求近似数》教案(表格版) | 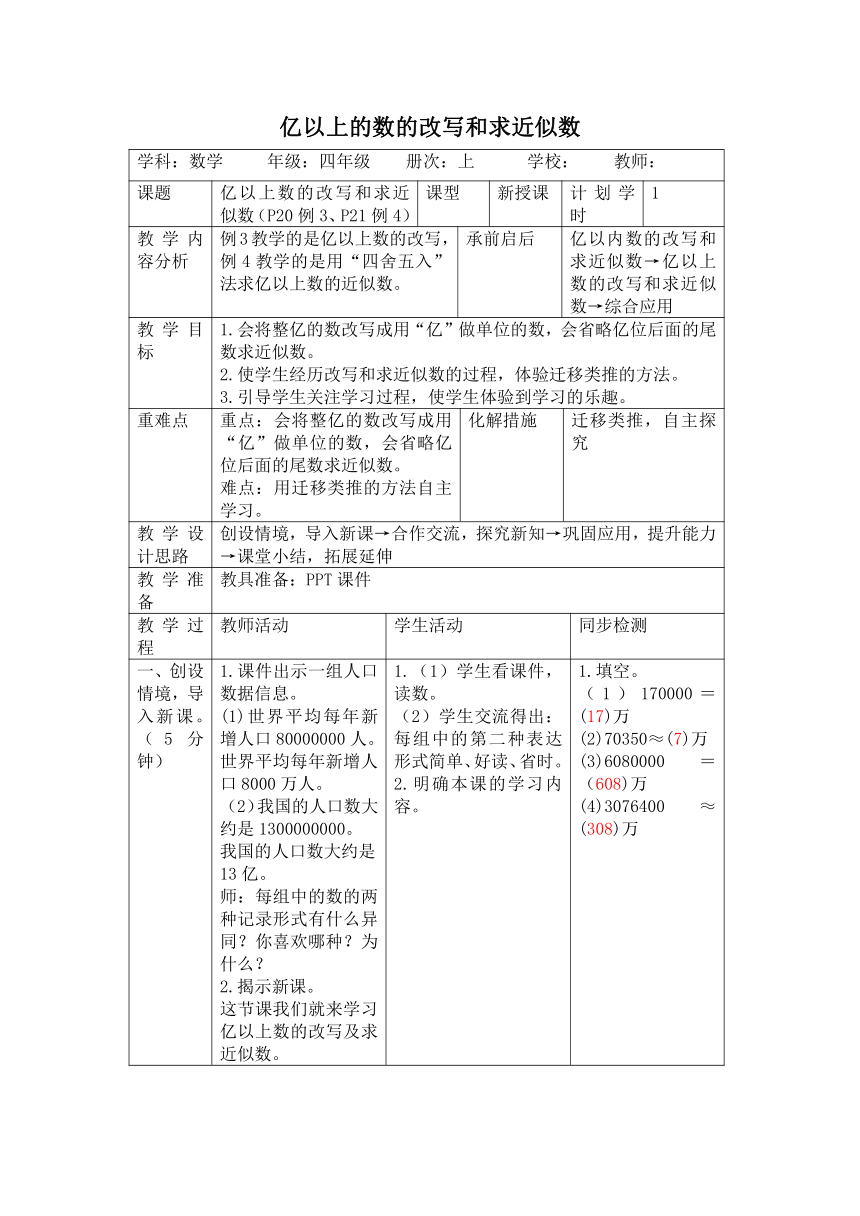 | |
| 格式 | zip | ||
| 文件大小 | 14.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-22 13:10:42 | ||
图片预览

文档简介
亿以上的数的改写和求近似数
学科:数学 年级:四年级 册次:上 学校: 教师:
课题
亿以上数的改写和求近似数(P20例3、P21例4)
课型
新授课
计划学时
1
教学内容分析
例3教学的是亿以上数的改写,例4教学的是用“四舍五入”法求亿以上数的近似数。
承前启后
亿以内数的改写和求近似数→亿以上数的改写和求近似数→综合应用
教学目标
1.会将整亿的数改写成用“亿”做单位的数,会省略亿位后面的尾数求近似数。
2.使学生经历改写和求近似数的过程,体验迁移类推的方法。
3.引导学生关注学习过程,使学生体验到学习的乐趣。
重难点
重点:会将整亿的数改写成用“亿”做单位的数,会省略亿位后面的尾数求近似数。
难点:用迁移类推的方法自主学习。
化解措施
迁移类推,自主探究
教学设计思路
创设情境,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教具准备:PPT课件
教学过程
教师活动
学生活动
同步检测
一、创设情境,导入新课。(5分钟)
1.课件出示一组人口数据信息。
(1)世界平均每年新增人口80000000人。
世界平均每年新增人口8000万人。
(2)我国的人口数大约是1300000000。
我国的人口数大约是13亿。
师:每组中的数的两种记录形式有什么异同?你喜欢哪种?为什么?
2.揭示新课。
这节课我们就来学习亿以上数的改写及求近似数。
1.(1)学生看课件,读数。
(2)学生交流得出:每组中的第二种表达形式简单、好读、省时。
2.明确本课的学习内容。
1.填空。
(1)170000=(17)万
(2)70350≈(7)万
(3)6080000=(608)万
(4)3076400≈(308)万
二、合作交流,探究新知。(20分钟)
1.教学亿以上数的改写。
(1)多媒体课件出示:
8000000 800万
1300000000 13亿
7000000000 70亿
仔细观察,说说每组数据是否相等。师:是如何改写的?
(2)出示例3,引导学生尝试把整亿数改写成用“亿”做单位的数。
(3)引导学生归纳亿以上的数的改写方法。
2.教学省略亿位后面的尾数,求近似数的方法。
(1) 课件出示例4,引导学生迁移旧知,思考省略亿位后面的尾数,求近似数的方法。
1034500000≈( )亿
9876540000≈( )亿
(2)尝试改写,交流汇报。
(3)师生共同总结省略亿位后面的尾数,求近似数的方法。
1.(1)学生观察得出:每组数据的数值是相等的,只是计数单位不同。
根据亿以内数的改写方法,试着说一说亿以上数的改写方法。
(2)独立完成,小组内交流、汇报。
1000000000= 10亿
530500000000=5305亿
(3)学生交流讨论得出:先分级,找到亿位,去掉亿位后面的8个0,再加一个亿字。
2.(1)明确题意,回忆亿以内的数求近似数的方法,讨论:亿以上的数该如何省略亿位后面的尾数,求近似数。
(2)学生独立改写,汇报改写结果。
1034500000≈( 10 )亿
9876540000≈( 99 )亿
(3)用规范的语言总结: 先分级,看千万位上的数是否满5,然后按照“四舍五入”法求出近似数。
2.把下面各数改写成用“亿”做单位的数。
(1)800000000=(8)亿
(2)42000000000=(420)亿
(3)8800000000=(88)亿
(4)10500000000=(105)亿
3.省略下面各数亿位后面的尾数,写出近似数。
(1)548000000≈(5)亿
(2)3795000000≈(38)亿
(3)690000000≈(7)亿
(4)3058000000≈(31)亿
(5)29970000000≈(300)亿
(6)9988520000≈(100)亿
三、巩固应用,提升能力。(10分钟)
1.完成教材第20页“做一做”第3题。
2.完成教材第21页“做一做”。
独立完成相关作业,全班交流、订正。
4. 98□5640140≈99亿,□里最大能填(9),最小能填(5)。
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2. 省略亿位后面的尾数求近似数时,是“四舍”还是“五入”要看千万位上的数,也就是省略部分最高位上的数。“五入”时不要忘记进1,有时还会遇到连续进位的情况。
教师个人补充意见:
板书设计
亿以上数的改写和求近似数
整亿的改写:先分级,找到亿位,去掉后面的8个0,再在末尾添上一个“亿”字,用“=”连接。
求近似数:先分级,看千万位,然后按照“四舍五入”法求出近似数,用“≈”连接。
培优作业
一个数四舍五入后的近似数是9亿,这个数最大是多少?最小是多少?
这个数最大是949999999,最小是850000000。
名师点睛
非整亿数的改写可类比非整万数的改写,通过类比、归纳、总结出非整亿数的改写方法。
微课设计点
教师可围绕“非整亿数的改写”设计微课。
学科:数学 年级:四年级 册次:上 学校: 教师:
课题
亿以上数的改写和求近似数(P20例3、P21例4)
课型
新授课
计划学时
1
教学内容分析
例3教学的是亿以上数的改写,例4教学的是用“四舍五入”法求亿以上数的近似数。
承前启后
亿以内数的改写和求近似数→亿以上数的改写和求近似数→综合应用
教学目标
1.会将整亿的数改写成用“亿”做单位的数,会省略亿位后面的尾数求近似数。
2.使学生经历改写和求近似数的过程,体验迁移类推的方法。
3.引导学生关注学习过程,使学生体验到学习的乐趣。
重难点
重点:会将整亿的数改写成用“亿”做单位的数,会省略亿位后面的尾数求近似数。
难点:用迁移类推的方法自主学习。
化解措施
迁移类推,自主探究
教学设计思路
创设情境,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教具准备:PPT课件
教学过程
教师活动
学生活动
同步检测
一、创设情境,导入新课。(5分钟)
1.课件出示一组人口数据信息。
(1)世界平均每年新增人口80000000人。
世界平均每年新增人口8000万人。
(2)我国的人口数大约是1300000000。
我国的人口数大约是13亿。
师:每组中的数的两种记录形式有什么异同?你喜欢哪种?为什么?
2.揭示新课。
这节课我们就来学习亿以上数的改写及求近似数。
1.(1)学生看课件,读数。
(2)学生交流得出:每组中的第二种表达形式简单、好读、省时。
2.明确本课的学习内容。
1.填空。
(1)170000=(17)万
(2)70350≈(7)万
(3)6080000=(608)万
(4)3076400≈(308)万
二、合作交流,探究新知。(20分钟)
1.教学亿以上数的改写。
(1)多媒体课件出示:
8000000 800万
1300000000 13亿
7000000000 70亿
仔细观察,说说每组数据是否相等。师:是如何改写的?
(2)出示例3,引导学生尝试把整亿数改写成用“亿”做单位的数。
(3)引导学生归纳亿以上的数的改写方法。
2.教学省略亿位后面的尾数,求近似数的方法。
(1) 课件出示例4,引导学生迁移旧知,思考省略亿位后面的尾数,求近似数的方法。
1034500000≈( )亿
9876540000≈( )亿
(2)尝试改写,交流汇报。
(3)师生共同总结省略亿位后面的尾数,求近似数的方法。
1.(1)学生观察得出:每组数据的数值是相等的,只是计数单位不同。
根据亿以内数的改写方法,试着说一说亿以上数的改写方法。
(2)独立完成,小组内交流、汇报。
1000000000= 10亿
530500000000=5305亿
(3)学生交流讨论得出:先分级,找到亿位,去掉亿位后面的8个0,再加一个亿字。
2.(1)明确题意,回忆亿以内的数求近似数的方法,讨论:亿以上的数该如何省略亿位后面的尾数,求近似数。
(2)学生独立改写,汇报改写结果。
1034500000≈( 10 )亿
9876540000≈( 99 )亿
(3)用规范的语言总结: 先分级,看千万位上的数是否满5,然后按照“四舍五入”法求出近似数。
2.把下面各数改写成用“亿”做单位的数。
(1)800000000=(8)亿
(2)42000000000=(420)亿
(3)8800000000=(88)亿
(4)10500000000=(105)亿
3.省略下面各数亿位后面的尾数,写出近似数。
(1)548000000≈(5)亿
(2)3795000000≈(38)亿
(3)690000000≈(7)亿
(4)3058000000≈(31)亿
(5)29970000000≈(300)亿
(6)9988520000≈(100)亿
三、巩固应用,提升能力。(10分钟)
1.完成教材第20页“做一做”第3题。
2.完成教材第21页“做一做”。
独立完成相关作业,全班交流、订正。
4. 98□5640140≈99亿,□里最大能填(9),最小能填(5)。
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2. 省略亿位后面的尾数求近似数时,是“四舍”还是“五入”要看千万位上的数,也就是省略部分最高位上的数。“五入”时不要忘记进1,有时还会遇到连续进位的情况。
教师个人补充意见:
板书设计
亿以上数的改写和求近似数
整亿的改写:先分级,找到亿位,去掉后面的8个0,再在末尾添上一个“亿”字,用“=”连接。
求近似数:先分级,看千万位,然后按照“四舍五入”法求出近似数,用“≈”连接。
培优作业
一个数四舍五入后的近似数是9亿,这个数最大是多少?最小是多少?
这个数最大是949999999,最小是850000000。
名师点睛
非整亿数的改写可类比非整万数的改写,通过类比、归纳、总结出非整亿数的改写方法。
微课设计点
教师可围绕“非整亿数的改写”设计微课。
