北师大版初中数学九年级上册知识讲解,巩固练习(教学资料,补习资料):第16讲 相似三角形的性质及应用(基础)(含答案)
文档属性
| 名称 | 北师大版初中数学九年级上册知识讲解,巩固练习(教学资料,补习资料):第16讲 相似三角形的性质及应用(基础)(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 252.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-22 17:22:05 | ||
图片预览




文档简介
相似三角形的性质及应用--知识讲解(基础)
【学习目标】
1、探索相似三角形的性质,能运用性质进行有关计算;
2、通过典型实例认识现实生活中物体的相似,能运用图形相似的知识解决一些简单的实际问题(如何把实际问题抽象为数学问题).
【要点梳理】
要点一、相似三角形的应用
1.测量高度
测量不能到达顶部的物体的高度,通常使用“在同一时刻物高与影长的比例相等”的原理解决.
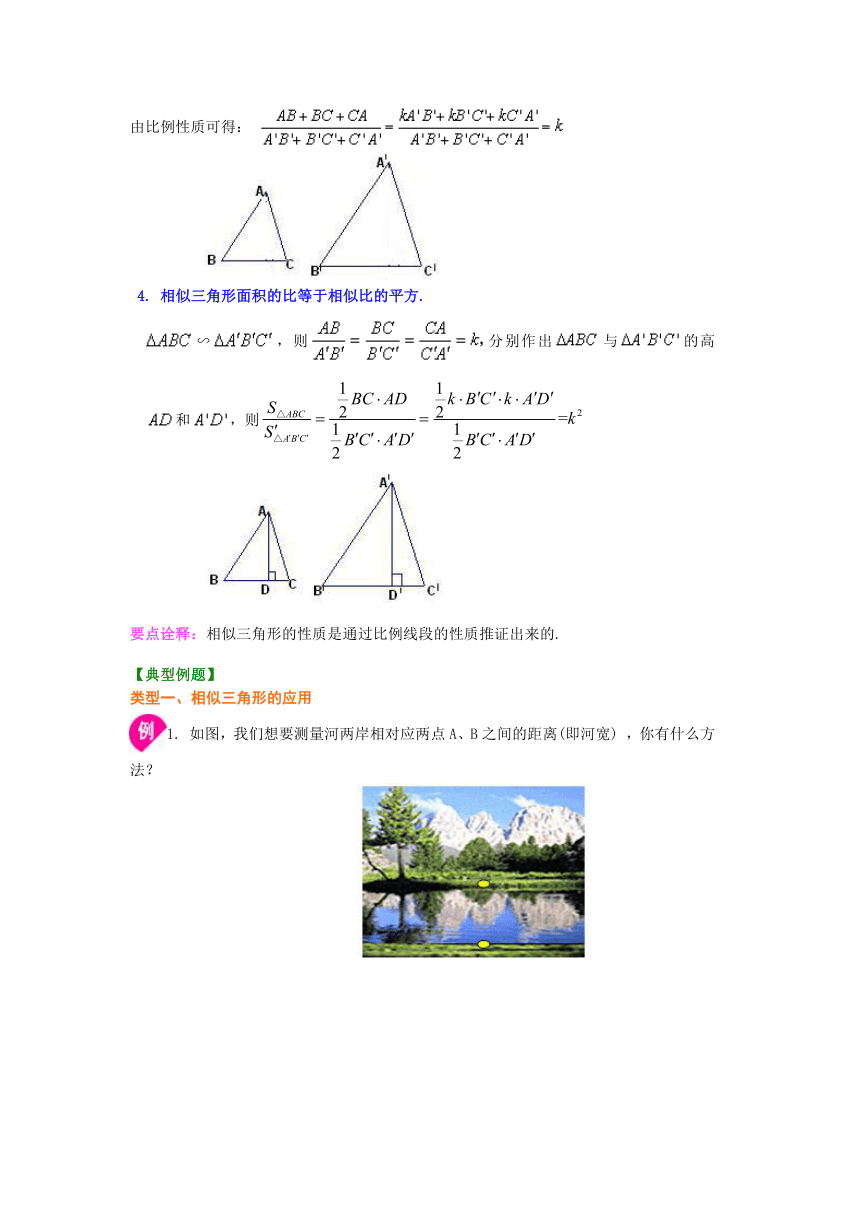
要点诠释:测量旗杆的高度的几种方法:
平面镜测量法 影子测量法 手臂测量法 标杆测量法
2.测量距离
测量不能直接到达的两点间的距离,常构造如下两种相似三角形求解。 1.如甲图所示,通常可先测量图中的线段DC、BD、CE的距离(长度),根据相似三角形的性质,求出AB的长.
2.如乙图所示,可先测AC、DC及DE的长,再根据相似三角形的性质计算AB的长. /
要点诠释:
1.比例尺:表示图上距离比实地距离缩小的程度,比例尺= 图上距离/ 实际距离; 2.太阳离我们非常遥远,因此可以把太阳光近似看成平行光线.在同一时刻,两物体影子之比等于其对应高的比; 3.视点:观察事物的着眼点(一般指观察者眼睛的位置);
4. 仰(俯)角:观察者向上(下)看时,视线与水平方向的夹角.
要点二、相似三角形的性质
1.相似三角形的对应角相等,对应边的比相等.
2. 相似三角形中的重要线段的比等于相似比.
相似三角形对应高,对应中线,对应角平分线的比都等于相似比.
要点诠释:要特别注意“对应”两个字,在应用时,要注意找准对应线段.
3. 相似三角形周长的比等于相似比.
/∽/,则/
由比例性质可得: /
/
4. 相似三角形面积的比等于相似比的平方.
/∽/,则/分别作出/与/的高/和/,则/
要点诠释:相似三角形的性质是通过比例线段的性质推证出来的.
【典型例题】
类型一、相似三角形的应用
/1. 如图,我们想要测量河两岸相对应两点A、B之间的距离(即河宽) ,你有什么方法? / /
【答案与解析】如上图,先从B点出发与AB成90°角方向走50m到O处立一标杆,然后方向不变,继续向前走10m到C处,在C处转90°,沿CD方向再走17m到达D处,使得A、O、D在同一条直线上.那么A、B之间的距离是多少? ∵AB⊥BC,CD⊥BC, ∴∠ABO=∠DCO=90°. 又 ∵ ∠AOB=∠DOC, ∴△AOB∽△DOC. ∴/. ∵BO=50m,CO=10m,CD=17m, ∴AB=85m. 即河宽为85m.
【总结升华】这是一道测量河宽的实际问题,还可以借用相似三角形的对应边的比 相等,比例式中四条线段,测出了三条线段的长,必能求出第四条.
/2. 如图:小明欲测量一座古塔的高度,他站在该塔的影子上前后移动,直到他本身影子的顶端正好与塔的影子的顶端重叠,此时他距离该塔18 m,已知小明的身高是1.6 m,他的影长是2 m. (1)图中△ABC与△ADE是否相似?为什么? (2)求古塔的高度. / 【思路点拨】本题考查的是相似三角形的实际应用,要注意的是小明和古塔都与地面垂直,是平行的.
【答案与解析】(1)△ABC∽△ADE. ∵BC⊥AE,DE⊥AE,∴∠ACB=∠AED=90°. ∵∠A=∠A,∴△ABC∽△ADE . (2)由(1)得△ABC∽△ADE, ∴/. ∵AC=2m,AE=2+18=20m,BC=1.6m, ∴/. ∴DE=16m, 即古塔的高度为16m.
【总结升华】解决相似三角形的实际应用题的关键是题中相似三角形的确定.
举一反三 【变式】小明把一个排球打在离他2米远的地上,排球反弹后碰到墙上,如果他跳起来击排球时的高度是1.8米,排球落地点离墙的距离是7米,假设排球一直沿直线运动,那么排球能碰到墙上离地多高的地方?
【答案】
如图,∵AB=1.8米,AP=2米,PC=7米,作PQ⊥AC,
根据物理学原理知∠BPQ=∠QPD,则∠APB=∠CPD,
∠BAP=∠DCP=90°,
∴ △ABP∽△CDP,
∴/,
即/,
∴DC=6.3米.
即球能碰到墙上离地6.3米高的地方.
类型二、相似三角形的性质
/3. (2019?随州)如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
/
A.1:3 B.1:4 C.1:5 D.1:25
【思路点拨】根据相似三角形的判定定理得到△DOE∽△COA,根据相似三角形的性质定理得到/=/,/=/=/,结合图形得到/=/,得到答案.
【答案】B.
【解析】
解:∵DE∥AC,
∴△DOE∽△COA,又S△DOE:S△COA=1:25,
∴/=/,
∵DE∥AC,
∴/=/=/,
∴/=/,
∴S△BDE与S△CDE的比是1:4,
故选:B.
【总结升华】本题考查的是相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.
举一反三
【变式】(2018?铜仁市)如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
/
A.3:4 B. 9:16 C. 9:1 D. 3:1
【答案】B.
提示:∵四边形ABCD为平行四边形,
∴DC∥AB,
∴△DFE∽△BFA,
∵DE:EC=3:1,
∴DE:DC=1=3:4,
∴DE:AB=3:4,
∴S△DFE:S△BFA=9:16.
故选:B.
/4.如图所示,已知△ABC中,AD是高,矩形EFGH内接于△ABC中,且长边FG在BC上,矩形相邻两边的比为1:2,若BC=30cm,AD=10cm.求矩形EFGH的面积. /
【思路点拨】相似三角形对应的高,中线,角分线对应成比例.
【答案与解析】∵ 四边形EFGH是矩形,∴ EH∥BC, ∴ △AEH∽△ABC. ∵ AD⊥BC,
∴ AD⊥EH,MD=EF. ∵ 矩形两邻边之比为1:2,
设EF=xcm,则EH=2xcm. 由相似三角形对应高的比等于相似比,得/, ∴ /,
∴ /,
∴/. ∴ EF=6cm,EH=12cm.. ∴/.
【总结升华】解决有关三角形的内接矩形、内接正方形的计算问题,经常利用相似三角形“对应高的比等于相似比”和“面积比等于相似比的平方”的性质,若图中没有高可以先作出高.
举一反三:
【变式】有同一三角形地块的甲、乙两地图,比例尺分别为1∶200和1∶500,求:甲地图与乙地图的相似比和面积比. 【答案】设原地块为△ABC,地块在甲图上为△A1B1C1,在乙图上为△A2B2C2. ∴ △ABC∽△A1B1C1∽△A2B2C2 且/,/, ∴/, ∴/.
相似三角形的性质及应用--巩固练习(基础)
【巩固练习】
一、选择题
1.(2018?酒泉)如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
/
A./ B. / C. / D./
2. (2019?临夏州)如果两个相似三角形的面积比是1:4,那么它们的周长比是( )
A.1:16 B.1:4 C.1:6 D.1:2
3.某校有两块相似的多边形草坪,其面积比为9∶4,其中一块草坪的周长是36米,则另一块草坪的周长是( ).
A.24米 B.54米 C.24米或54米 D.36米或54米
4. 图为△ABC与△DEC重叠的情形,其中E在BC上,AC交DE于F点,且AB// DE.若△ABC与△DEC的面积相等,且EF=9,AB=12,则DF=( ).
?A.3 B.7 C.12 D.15? /
5.如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米, 那么该古城墙的高度是( ).
A.6米 B.8米 C.18米 D.24米
6. 要把一个三角形的面积扩大到原来面积的8倍,而它的形状不变,那么它的边长要增大到原来的( )倍.
A.2 B.4 C.2/ D.64
二、填空题/
7. 如图所示,为了测量一棵树AB的高度,测量者在D点立一高CD=2m的标杆,现测量者从E处可以看到杆顶C与树顶A在同一条直线上,如果测得BD=20m,FD=4m,EF=1.8m,则树AB的高度为______m. /
8. 已知两个相似三角形的相似比为/,面积之差为25/,则较大三角形的面积为______/.? 9.(2018?吉林)如图,利用标杆BE测量建筑物的高度,标杆BE高1.5m,测得AB=2m,BC=14cm,则楼高CD为 m.
/
10. (2019?徐州)如图,△ABC中,D、E分别为AB、AC的中点,则△ADE与△ABC的面积比为 .
/
11.如图,在平行四边形ABCD中,点E为CD上一点,DE:CE=2:3,连接AE,BE,BD,且AE,BD交于点F,则/________________.
/
12.把一个三角形改做成和它相似的三角形,如果面积缩小到原来的/倍,那么边长应缩小到原来的________倍.
三、解答题
13. 一位同学想利用树影测量树高,他在某一时刻测得长为1m的竹竿影长0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,如图,他先测得留在墙上的影高1.2m,又测得地面部分的影长2.7m,他求得树高是多少?
/
14.(2018?蓬溪县校级模拟)小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米,请你帮助小红测量出大楼AB的高度(注:入射角=反射角).
/
15. 在正方形/中,/是/上一动点,(与/不重合),使/为直角,/交正方形一边所在直线于点/. (1)找出与/相似的三角形. (2)当/位于/的中点时,与/相似的三角形周长为/,则/的周长为多少? /
【答案与解析】
一.选择题
1.【答案】D.
【解析】∵S△BDE:S△CDE=1:3,∴BE:EC=1:3;∴BE:BC=1:4;
∵DE∥AC,∴△DOE∽△AOC,
∴/=/,∴S△DOE:S△AOC=/=/,
故选D.
2.【答案】D.
【解析】∵两个相似三角形的面积比是1:4,
∴两个相似三角形的相似比是1:2,
∴两个相似三角形的周长比是1:2.
3.【答案】C.
4.【答案】B.
5.【答案】B.
【解析】提示:入射角等于反射角,所以△ABP∽△CDP.
6.【答案】C.
【解析】提示:面积比等于相似比的平方.
二.填空题
7.【答案】3.
8.【答案】45cm2.
9.【答案】12.
10.【答案】1:4.
【解析】∵D、E分别为AB、AC的中点,
∴DE=/BC,DE∥BC,
∴△ADE∽△ABC,
∴/=(/)2=/.
11.【答案】4:10:25
【解析】∵ 平行四边形ABCD,∴△DEF∽△BAF,∴/∵DE:EC=2:3,∴DE:DC=2:5,即DE:AB=2:5,∴/∵△DEF与△BEF是同高的三角形,∴//
12.【答案】/.
三.综合题
13.【解析】作CE∥DA交AB于E,设树高是xm,
∵ 长为1m的竹竿影长0.9m
∴ /
即 x=4.2m
/
14.【解析】解:如图,
∵根据反射定律知:∠FEB=∠FED,
∴∠BEA=∠DEC
∵∠BAE=∠DCE=90°
∴△BAE∽△DCE
∴/;
∵CE=2.5米,DC=1.6米,
∴/;
∴AB=12.8
答:大楼AB的高为12.8米.
15.【解析】(1)与△BPC相似的图形可以是图(1),(2)两种情况:
△PDE∽△BCP,△PCE∽△BCP,△BPE∽△BCP.
(2)①如图(1),当点P位于CD的中点时,若另一直角边与AD交于点E,
则/
∵ △PDE∽△BCP
∴ △PDE与△BCP的周长比是1:2
∴ △BCP的周长是2a.
②如图(2),当点P位于CD的中点时,若另一直角边与BC延长线交于点E时,
则/,
∵ △PCE∽△BCP
∴ △PCE与△BCP的周长比是1:2
∴ △BCP的周长是2a.
③如图(2),当点P位于CD的中点时,若另一直角边与BC延长线交于点E时,
∴ /
∵ △BPE∽△BCP
∴ △BPE与△BCP的周长比是/:2,
∴ △BCP的周长是/.
/
【学习目标】
1、探索相似三角形的性质,能运用性质进行有关计算;
2、通过典型实例认识现实生活中物体的相似,能运用图形相似的知识解决一些简单的实际问题(如何把实际问题抽象为数学问题).
【要点梳理】
要点一、相似三角形的应用
1.测量高度
测量不能到达顶部的物体的高度,通常使用“在同一时刻物高与影长的比例相等”的原理解决.
要点诠释:测量旗杆的高度的几种方法:
平面镜测量法 影子测量法 手臂测量法 标杆测量法
2.测量距离
测量不能直接到达的两点间的距离,常构造如下两种相似三角形求解。 1.如甲图所示,通常可先测量图中的线段DC、BD、CE的距离(长度),根据相似三角形的性质,求出AB的长.
2.如乙图所示,可先测AC、DC及DE的长,再根据相似三角形的性质计算AB的长. /
要点诠释:
1.比例尺:表示图上距离比实地距离缩小的程度,比例尺= 图上距离/ 实际距离; 2.太阳离我们非常遥远,因此可以把太阳光近似看成平行光线.在同一时刻,两物体影子之比等于其对应高的比; 3.视点:观察事物的着眼点(一般指观察者眼睛的位置);
4. 仰(俯)角:观察者向上(下)看时,视线与水平方向的夹角.
要点二、相似三角形的性质
1.相似三角形的对应角相等,对应边的比相等.
2. 相似三角形中的重要线段的比等于相似比.
相似三角形对应高,对应中线,对应角平分线的比都等于相似比.
要点诠释:要特别注意“对应”两个字,在应用时,要注意找准对应线段.
3. 相似三角形周长的比等于相似比.
/∽/,则/
由比例性质可得: /
/
4. 相似三角形面积的比等于相似比的平方.
/∽/,则/分别作出/与/的高/和/,则/
要点诠释:相似三角形的性质是通过比例线段的性质推证出来的.
【典型例题】
类型一、相似三角形的应用
/1. 如图,我们想要测量河两岸相对应两点A、B之间的距离(即河宽) ,你有什么方法? / /
【答案与解析】如上图,先从B点出发与AB成90°角方向走50m到O处立一标杆,然后方向不变,继续向前走10m到C处,在C处转90°,沿CD方向再走17m到达D处,使得A、O、D在同一条直线上.那么A、B之间的距离是多少? ∵AB⊥BC,CD⊥BC, ∴∠ABO=∠DCO=90°. 又 ∵ ∠AOB=∠DOC, ∴△AOB∽△DOC. ∴/. ∵BO=50m,CO=10m,CD=17m, ∴AB=85m. 即河宽为85m.
【总结升华】这是一道测量河宽的实际问题,还可以借用相似三角形的对应边的比 相等,比例式中四条线段,测出了三条线段的长,必能求出第四条.
/2. 如图:小明欲测量一座古塔的高度,他站在该塔的影子上前后移动,直到他本身影子的顶端正好与塔的影子的顶端重叠,此时他距离该塔18 m,已知小明的身高是1.6 m,他的影长是2 m. (1)图中△ABC与△ADE是否相似?为什么? (2)求古塔的高度. / 【思路点拨】本题考查的是相似三角形的实际应用,要注意的是小明和古塔都与地面垂直,是平行的.
【答案与解析】(1)△ABC∽△ADE. ∵BC⊥AE,DE⊥AE,∴∠ACB=∠AED=90°. ∵∠A=∠A,∴△ABC∽△ADE . (2)由(1)得△ABC∽△ADE, ∴/. ∵AC=2m,AE=2+18=20m,BC=1.6m, ∴/. ∴DE=16m, 即古塔的高度为16m.
【总结升华】解决相似三角形的实际应用题的关键是题中相似三角形的确定.
举一反三 【变式】小明把一个排球打在离他2米远的地上,排球反弹后碰到墙上,如果他跳起来击排球时的高度是1.8米,排球落地点离墙的距离是7米,假设排球一直沿直线运动,那么排球能碰到墙上离地多高的地方?
【答案】
如图,∵AB=1.8米,AP=2米,PC=7米,作PQ⊥AC,
根据物理学原理知∠BPQ=∠QPD,则∠APB=∠CPD,
∠BAP=∠DCP=90°,
∴ △ABP∽△CDP,
∴/,
即/,
∴DC=6.3米.
即球能碰到墙上离地6.3米高的地方.
类型二、相似三角形的性质
/3. (2019?随州)如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
/
A.1:3 B.1:4 C.1:5 D.1:25
【思路点拨】根据相似三角形的判定定理得到△DOE∽△COA,根据相似三角形的性质定理得到/=/,/=/=/,结合图形得到/=/,得到答案.
【答案】B.
【解析】
解:∵DE∥AC,
∴△DOE∽△COA,又S△DOE:S△COA=1:25,
∴/=/,
∵DE∥AC,
∴/=/=/,
∴/=/,
∴S△BDE与S△CDE的比是1:4,
故选:B.
【总结升华】本题考查的是相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.
举一反三
【变式】(2018?铜仁市)如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
/
A.3:4 B. 9:16 C. 9:1 D. 3:1
【答案】B.
提示:∵四边形ABCD为平行四边形,
∴DC∥AB,
∴△DFE∽△BFA,
∵DE:EC=3:1,
∴DE:DC=1=3:4,
∴DE:AB=3:4,
∴S△DFE:S△BFA=9:16.
故选:B.
/4.如图所示,已知△ABC中,AD是高,矩形EFGH内接于△ABC中,且长边FG在BC上,矩形相邻两边的比为1:2,若BC=30cm,AD=10cm.求矩形EFGH的面积. /
【思路点拨】相似三角形对应的高,中线,角分线对应成比例.
【答案与解析】∵ 四边形EFGH是矩形,∴ EH∥BC, ∴ △AEH∽△ABC. ∵ AD⊥BC,
∴ AD⊥EH,MD=EF. ∵ 矩形两邻边之比为1:2,
设EF=xcm,则EH=2xcm. 由相似三角形对应高的比等于相似比,得/, ∴ /,
∴ /,
∴/. ∴ EF=6cm,EH=12cm.. ∴/.
【总结升华】解决有关三角形的内接矩形、内接正方形的计算问题,经常利用相似三角形“对应高的比等于相似比”和“面积比等于相似比的平方”的性质,若图中没有高可以先作出高.
举一反三:
【变式】有同一三角形地块的甲、乙两地图,比例尺分别为1∶200和1∶500,求:甲地图与乙地图的相似比和面积比. 【答案】设原地块为△ABC,地块在甲图上为△A1B1C1,在乙图上为△A2B2C2. ∴ △ABC∽△A1B1C1∽△A2B2C2 且/,/, ∴/, ∴/.
相似三角形的性质及应用--巩固练习(基础)
【巩固练习】
一、选择题
1.(2018?酒泉)如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,若S△BDE:S△CDE=1:3,则S△DOE:S△AOC的值为( )
/
A./ B. / C. / D./
2. (2019?临夏州)如果两个相似三角形的面积比是1:4,那么它们的周长比是( )
A.1:16 B.1:4 C.1:6 D.1:2
3.某校有两块相似的多边形草坪,其面积比为9∶4,其中一块草坪的周长是36米,则另一块草坪的周长是( ).
A.24米 B.54米 C.24米或54米 D.36米或54米
4. 图为△ABC与△DEC重叠的情形,其中E在BC上,AC交DE于F点,且AB// DE.若△ABC与△DEC的面积相等,且EF=9,AB=12,则DF=( ).
?A.3 B.7 C.12 D.15? /
5.如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米, 那么该古城墙的高度是( ).
A.6米 B.8米 C.18米 D.24米
6. 要把一个三角形的面积扩大到原来面积的8倍,而它的形状不变,那么它的边长要增大到原来的( )倍.
A.2 B.4 C.2/ D.64
二、填空题/
7. 如图所示,为了测量一棵树AB的高度,测量者在D点立一高CD=2m的标杆,现测量者从E处可以看到杆顶C与树顶A在同一条直线上,如果测得BD=20m,FD=4m,EF=1.8m,则树AB的高度为______m. /
8. 已知两个相似三角形的相似比为/,面积之差为25/,则较大三角形的面积为______/.? 9.(2018?吉林)如图,利用标杆BE测量建筑物的高度,标杆BE高1.5m,测得AB=2m,BC=14cm,则楼高CD为 m.
/
10. (2019?徐州)如图,△ABC中,D、E分别为AB、AC的中点,则△ADE与△ABC的面积比为 .
/
11.如图,在平行四边形ABCD中,点E为CD上一点,DE:CE=2:3,连接AE,BE,BD,且AE,BD交于点F,则/________________.
/
12.把一个三角形改做成和它相似的三角形,如果面积缩小到原来的/倍,那么边长应缩小到原来的________倍.
三、解答题
13. 一位同学想利用树影测量树高,他在某一时刻测得长为1m的竹竿影长0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,如图,他先测得留在墙上的影高1.2m,又测得地面部分的影长2.7m,他求得树高是多少?
/
14.(2018?蓬溪县校级模拟)小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米,请你帮助小红测量出大楼AB的高度(注:入射角=反射角).
/
15. 在正方形/中,/是/上一动点,(与/不重合),使/为直角,/交正方形一边所在直线于点/. (1)找出与/相似的三角形. (2)当/位于/的中点时,与/相似的三角形周长为/,则/的周长为多少? /
【答案与解析】
一.选择题
1.【答案】D.
【解析】∵S△BDE:S△CDE=1:3,∴BE:EC=1:3;∴BE:BC=1:4;
∵DE∥AC,∴△DOE∽△AOC,
∴/=/,∴S△DOE:S△AOC=/=/,
故选D.
2.【答案】D.
【解析】∵两个相似三角形的面积比是1:4,
∴两个相似三角形的相似比是1:2,
∴两个相似三角形的周长比是1:2.
3.【答案】C.
4.【答案】B.
5.【答案】B.
【解析】提示:入射角等于反射角,所以△ABP∽△CDP.
6.【答案】C.
【解析】提示:面积比等于相似比的平方.
二.填空题
7.【答案】3.
8.【答案】45cm2.
9.【答案】12.
10.【答案】1:4.
【解析】∵D、E分别为AB、AC的中点,
∴DE=/BC,DE∥BC,
∴△ADE∽△ABC,
∴/=(/)2=/.
11.【答案】4:10:25
【解析】∵ 平行四边形ABCD,∴△DEF∽△BAF,∴/∵DE:EC=2:3,∴DE:DC=2:5,即DE:AB=2:5,∴/∵△DEF与△BEF是同高的三角形,∴//
12.【答案】/.
三.综合题
13.【解析】作CE∥DA交AB于E,设树高是xm,
∵ 长为1m的竹竿影长0.9m
∴ /
即 x=4.2m
/
14.【解析】解:如图,
∵根据反射定律知:∠FEB=∠FED,
∴∠BEA=∠DEC
∵∠BAE=∠DCE=90°
∴△BAE∽△DCE
∴/;
∵CE=2.5米,DC=1.6米,
∴/;
∴AB=12.8
答:大楼AB的高为12.8米.
15.【解析】(1)与△BPC相似的图形可以是图(1),(2)两种情况:
△PDE∽△BCP,△PCE∽△BCP,△BPE∽△BCP.
(2)①如图(1),当点P位于CD的中点时,若另一直角边与AD交于点E,
则/
∵ △PDE∽△BCP
∴ △PDE与△BCP的周长比是1:2
∴ △BCP的周长是2a.
②如图(2),当点P位于CD的中点时,若另一直角边与BC延长线交于点E时,
则/,
∵ △PCE∽△BCP
∴ △PCE与△BCP的周长比是1:2
∴ △BCP的周长是2a.
③如图(2),当点P位于CD的中点时,若另一直角边与BC延长线交于点E时,
∴ /
∵ △BPE∽△BCP
∴ △BPE与△BCP的周长比是/:2,
∴ △BCP的周长是/.
/
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
