人教版高中数学必修三知识讲解,巩固练习(教学资料,补习资料):第02章 章末检测高一数学
文档属性
| 名称 | 人教版高中数学必修三知识讲解,巩固练习(教学资料,补习资料):第02章 章末检测高一数学 |  | |
| 格式 | zip | ||
| 文件大小 | 300.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-23 19:43:58 | ||
图片预览




文档简介
第二章 统计
章末检测
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.我校今年有1901名同学参加高考,从中随机抽取50名同学的总成绩进行分析,在这个调查中,下列叙述错误的是
A.总体是:1901名同学的总成绩
B.个体是:每一名同学
C.样本是:50名同学的总成绩
D.样本容量是:50
2.某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号,001,002,……,699,700.从中抽取70个样本,下图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第8个样本编号是
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
A.623 B.368 C.253 D.072
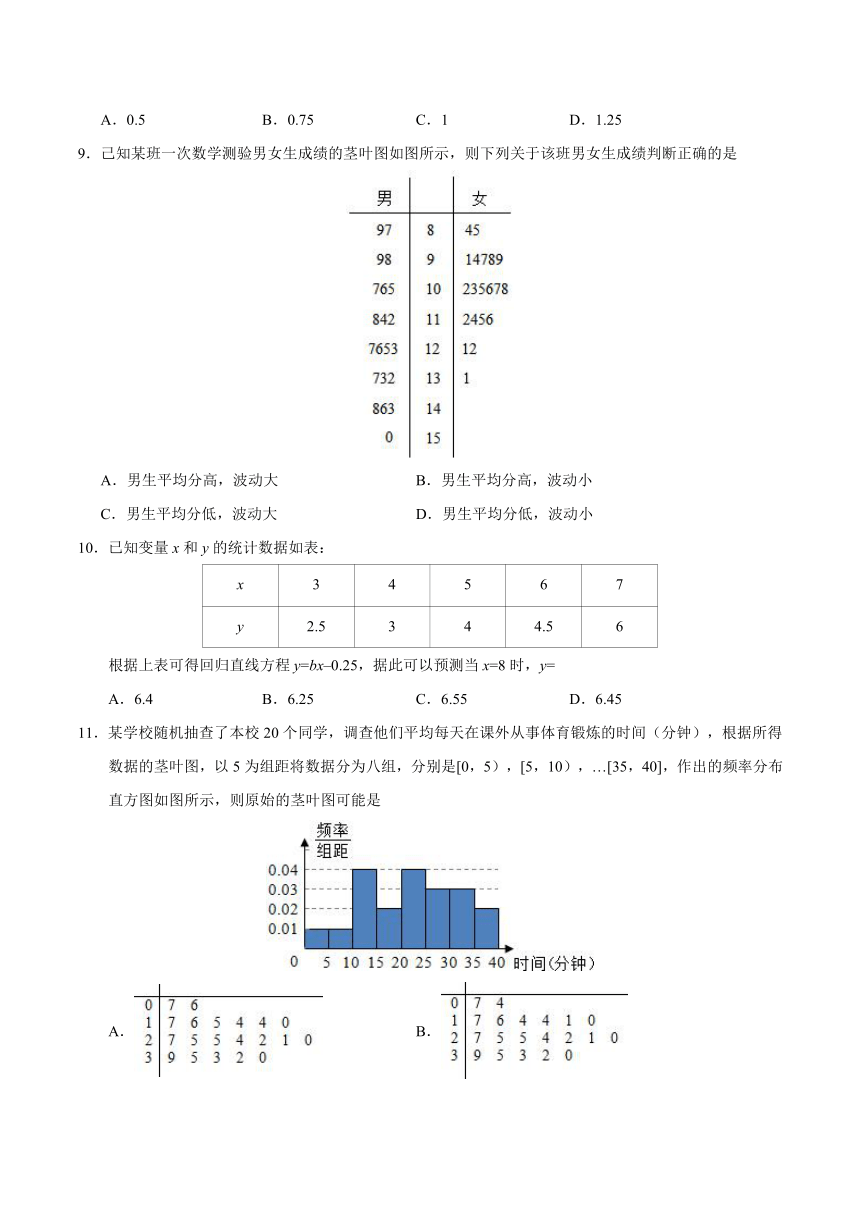
3.如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是
A.2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
B.与去年同期相比,2017年第一季度五个省的GDP总量均实现了增长
C.去年同期河南省的GDP总量不超过4000亿元
D.2017年第一季度GDP增速由高到低排位第5的是浙江省
4.在一次歌咏比赛中,七位裁判为一选手打出的分数如下:
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为
A.92,2.8 B.92,2 C.93,2 D.93,2.8
5.某校高中三个年级人数饼图如图所示,按年级用分层抽样的方法抽取一个样本,已知样本中高一年级学生有8人,则样本容量为
A.24 B.30 C.32 D.35
6.学校根据某班的期中考试成绩绘制了频率分布直方图(如图所示),根据图中所给的数据可知a+b=
A.0.024 B.0.036 C.0.06 D.0.6
7.从2010名学生中选取50名学生参加英语比赛,若采用下面的方法选取:先用简单随机抽样从2010人中剔除10人,剩下的2000人再按系统抽样的方法抽取50人,则在2010人中,每人入选的概率
A.不全相等 B.均不相等
C.都相等,且为 D.都相等,且为
8.某次知识竞赛中,四个参赛小队的初始积分都是10分,在答题过程中,各小队每答对1题加0.5分,若答题过程中四个小队答对的题数分别是3道,7道,7道,3道,则四个小组积分的方差为
A.0.5 B.0.75 C.1 D.1.25
9.己知某班一次数学测验男女生成绩的茎叶图如图所示,则下列关于该班男女生成绩判断正确的是
A.男生平均分高,波动大 B.男生平均分高,波动小
C.男生平均分低,波动大 D.男生平均分低,波动小
10.已知变量x和y的统计数据如表:
x
3
4
5
6
7
y
2.5
3
4
4.5
6
根据上表可得回归直线方程y=bx–0.25,据此可以预测当x=8时,y=
A.6.4 B.6.25 C.6.55 D.6.45
11.某学校随机抽查了本校20个同学,调查他们平均每天在课外从事体育锻炼的时间(分钟),根据所得数据的茎叶图,以5为组距将数据分为八组,分别是[0,5),[5,10),…[35,40],作出的频率分布直方图如图所示,则原始的茎叶图可能是
A. B.
C. D.
12.已知变量x,y之间的线性回归方程为,且变量x,y之间的一组相关数据如表所示,则下列说法错误的是
x
6
8
10
12
y
6
m
3
2
A.变量x,y之间呈现负相关关系
B.可以预测,当x=20时,y=–3.7
C.m=4
D.由表格数据可知,该回归直线必过点(9,4)
二、填空题:请将答案填在题中横线上.
13.某地区有600家商店,其中大型商店有60家,中型商店有150家,小型商店有390家,为了掌握各商店的营业情况,要从中抽取一个容量为40的样本,若采用分层抽样的方法,抽取的中型商店数是___________.
14.某单位有842名职工,现采用系统抽样方法抽出5%的人做问卷调查,剔除适当人数后从1开始随机编号,现抽取的人中,编号落在区间[481,720]内的人数为___________.
15.对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为___________.
16.人甲在某周五天的时间内,每天加工零件的个数用茎叶图表示如图(左边一列的数字表示零件个数的十位数,右边的数字表示零件个数的个位数),则该组数据的方差s2的值为___________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.某体育代表队有200名运动员,其中2名是种子选手.现从中抽取13名参加运动会,要求种子选手必须参加.请采用系统抽样的方法给出抽样过程.
18.篮球运动员甲在最近6场NBA比赛中所得分数的茎叶图如图所示,由于疏忽,茎叶图中的两个数据上出现了污渍,导致这两个数字无法辨认,但统计员记得除掉污渍2处的数字不影响整体中位数,且这六个数据的平均值为17.
(1)求污渍1,2处的数字;
(2)篮球运动员乙在最近6场NBA的比赛中所得分数为8,12,16,18,20,28.试分别以各自6场比赛得分的平均数与方差来分析这两名篮球运动员的发挥水平.
19.某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),[60,70),…[90,100]后得到如下频率分布直方图.
(1)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的平均分、众数、中位数;(小数点后保留一位有效数字)
(2)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则[70,80)分数段抽取的人数是多少?
20.下表是某地一家超市在2014年一月份某周的时间x与每天获得的利润y(单位:万元)的有关数据.
时间x
星期二
星期三
星期四
星期五
星期六
利润y
2
3
5
6
9
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程x+;
(3)估计星期日获得的利润为多少万元.
21.某个体服装店经营某种服装在某周内获纯利y(元)与该周每天销售这件服装件数x(件)之间有如下数据:
服装件数x(件)
3
4
5
6
7
8
9
某周内获纯利y(元)
66
69
73
81
89
90
91
(1)求,;
(2)若纯利y与每天销售这件服装件数x之间是线性相关的,求回归方程;
(3)若该店每天至少要获利200元,请你预测该店每天至少要销售这种服装多少件?
22.每年的4月23日是“世界读书日”,某校研究性学习小组为了解本校学生的阅读情况,随机调查了本校200名学生在这一天的阅读时间t(单位:分钟),将样本数据整理后绘制成如图的样本频率分布直方图.
(1)求a的值;
(2)试估计该学校所有学生在这一天的平均阅读时间;
(3)若用分层抽样的方法从这200名学生中,抽出25人参加交流会,则阅读时间为[30,40),[60,70]的两组中各抽取多少人?
参考答案
1
2
3
4
5
6
7
8
9
10
11
12
B
B
A
A
C
C
C
C
A
C
B
C
1.【答案】B
【解析】据题意总体是指1901名同学的总成绩,样本是指抽取的50名同学的总成绩,个体是指每一名同学的中考数学成绩,样本容量是50,故B错误.故选B.
2.【答案】B
【解析】从表中第5行第6列开始向右读取数据,得到的前8个编号分别是:253,313,457,007,328,623,072,368.则得到的第8个样本编号是368.故选B.
3.【答案】A
【解析】由2017年第一季度五省GDP情况图,知:在A中,2017年第一季度GDP总量和增速由高到低排位均居同一位的省有江苏和山东,共2个,故A错误;在B中,与去年同期相比,2017年第一季度五个省的GDP总量均实现了增长,故B正确;在C中,去年同期河南省的GDP总量不超过4000亿元,故C正确;在D中,2017年第一季度GDP增速由高到低排位第5的是浙江省,故D正确.故选A.
6.【答案】C
【解析】根据频率分布直方图得,(0.01+a+b+0.018+0.012)×10=1,解得a+b=0.06.故选C.
7.【答案】C
【解析】从2010名学生中选取50名学生参加英语比赛,按系统抽样的方法抽取50人,由于系统抽样是一个等可能抽样,故每个人入选的概率是,故选C.
8.【答案】C
【解析】根据题意,四个参赛小队的得分为11.5,13.5,13.5,11.5;计算平均数为×(11.5+13.5+13.5+11.5)=12.5,方差为s2=×[(11.5–12.5)2+(13.5–12.5)2+(13.5–12.5)2+(11.5–12.5)2]=1.故选C.
9.【答案】A
【解析】根据茎叶图中的数据知,男同学数学成绩比较分散,且高分较多,女同学数学成绩比较集中,且低分多些,根据样本数据的数字特征知这次测验中男生平均分高些,波动大.故选A.
10.【答案】C
【解析】样本平均数=5,=4,即4=5b–0.25,∴b=0.85,∴回归直线方程y=0.85x–0.25,当x=8时,y=0.85×8–0.25=6.55,故选C.
13.【答案】10
【解析】设抽取的中型商店数为x,则,解得x=10,故答案为:10.
14.【答案】12
【解析】∵某单位有842名职工,采用系统抽样方法抽出5%的人做问卷调查,剔除适当人数后从1开始随机编号,∴抽取人数为:840×5%=42人,即从20人中抽取1人,∴现抽取的人中,编号落在区间[481,720]内的人数为:=12人.故答案为:12.
15.【答案】100
【解析】根据频率分布直方图可知,三等品的数量是[(0.0125+0.025+0.0125)×5]×400=100(件).故答案为:100.
16.【答案】
【解析】由茎叶图得该组数据的平均数为:(18+17+22+21+22)=20,∴该组数据的方差为:s2=[(18–20)2+(17–20)2+(22–20)2+(21–20)2+(22–20)2]=.故答案为:.
17.【答案】详见解析.
【解析】第一步:将除种子选手外的198名运动员随机编号为001,002,…,198;
第二步:将编号按顺序分成11段,每段18个;
第三步:在第1段001,002,…,018这18个编号中用简单随机抽样抽出一个编号(如010)作为起始号码;
第四步:将编号为010,028,046,…,190的个体抽出,与种子选手一起参加该运动会.
(2)甲的得分的平均数为x甲=17,
甲的得分的方差为
[(8–17)2+(13–17)2+(15–17)2+(24–17)2+(27–17)2]=,
乙的得分的平均数为
x乙==17.
乙的得分的方差为
[(8–17)2+(12–17)2+(16–17)2+(18–17)2+(20–17)2+(28–17)2]=,
由于x甲=x乙,,
所以两人的平均水平相当,但是乙的得分波动更小,发挥更稳定,故乙发挥水平更好.
19.【答案】(1)平均分为71、众数为75、中位数为70.3;(2)6人.
【解析】(1)根据频率和为1,列方程得:
(0.01+0.015×2+a+0.025+0.005)×10=1,解得a=0.03;
估计该校高二年级学生政治成绩的平均分为:
(45×0.01+55×0.015+65×0.015+75×0.03+85×0.025+95×0.005)×10=71;
根据频率分布直方图,估计这40名学生期中政治成绩的众数为×(70+80)=75;
因为在频率分布直方图中
第一、二、三组的频率之和为(0.010+0.015×2)×10=0.4,
所以中位数为70+≈70.3;
(2)用分层抽样法,抽取容量为20的样本,在[70,80)内抽取的人数是:
20×0.03×10=6人.
20.【答案】(1)详见解析;(2)=1.7x–1.8;(3)星期日估计获得的利润为10.1万元.
【解析】(1)由x、y的数据可得对应的散点图为
从上图可知,这些点大致分布在一条直线附近,
故时间x与获得的利润y(万元)线性相关关系显著.
(3)当x=7时,=1.7×7–1.8=10.1(万元),
所以星期日估计获得的利润为10.1万元.
21.【答案】(1)=6,=80;(2)回归方程为y=x+;(3)每天销售件数x至少为32件.
【解析】(1)(3+4+5+6+7+8+9)=6,(66+69+73+81+89+90+91)=80,
(2)3×66+4×69+5×73+6×81+7×89+8×90+9×91=3487,
32+42+52+62+72+82+92=280,
∴b=,a=,
∴回归方程为y=x+;
(3)由x+≥200,∴x≥31,
∴估计每天销售件数x至少为32件.
22.【答案】(1)a=0.032;(2)43.8分钟;(3)阅读时间在[30,40)分钟的应选8人,阅读时间在[60,70]分钟的应选3人.
【解析】(1)由已知,得0.008×10+a×10+0.012×10×2+0.036+×10=1,
解得a=0.032.
(2)由样本的频率分布直方图,估计该学校所有学生在这一天的平均阅读时间为:
(分钟).
(3)阅读时间在[30,40)分钟的人数为200×0.032×10=64,
阅读时间在[60,70]分钟的人数为200×0.012×10=24,
用分层抽样选人的抽样比为,
∴阅读时间在[30,40)分钟的应选人,
阅读时间在[60,70]分钟的应选人.
章末检测
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.我校今年有1901名同学参加高考,从中随机抽取50名同学的总成绩进行分析,在这个调查中,下列叙述错误的是
A.总体是:1901名同学的总成绩
B.个体是:每一名同学
C.样本是:50名同学的总成绩
D.样本容量是:50
2.某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号,001,002,……,699,700.从中抽取70个样本,下图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第8个样本编号是
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
A.623 B.368 C.253 D.072
3.如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是
A.2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
B.与去年同期相比,2017年第一季度五个省的GDP总量均实现了增长
C.去年同期河南省的GDP总量不超过4000亿元
D.2017年第一季度GDP增速由高到低排位第5的是浙江省
4.在一次歌咏比赛中,七位裁判为一选手打出的分数如下:
90 89 90 95 93 94 93
去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为
A.92,2.8 B.92,2 C.93,2 D.93,2.8
5.某校高中三个年级人数饼图如图所示,按年级用分层抽样的方法抽取一个样本,已知样本中高一年级学生有8人,则样本容量为
A.24 B.30 C.32 D.35
6.学校根据某班的期中考试成绩绘制了频率分布直方图(如图所示),根据图中所给的数据可知a+b=
A.0.024 B.0.036 C.0.06 D.0.6
7.从2010名学生中选取50名学生参加英语比赛,若采用下面的方法选取:先用简单随机抽样从2010人中剔除10人,剩下的2000人再按系统抽样的方法抽取50人,则在2010人中,每人入选的概率
A.不全相等 B.均不相等
C.都相等,且为 D.都相等,且为
8.某次知识竞赛中,四个参赛小队的初始积分都是10分,在答题过程中,各小队每答对1题加0.5分,若答题过程中四个小队答对的题数分别是3道,7道,7道,3道,则四个小组积分的方差为
A.0.5 B.0.75 C.1 D.1.25
9.己知某班一次数学测验男女生成绩的茎叶图如图所示,则下列关于该班男女生成绩判断正确的是
A.男生平均分高,波动大 B.男生平均分高,波动小
C.男生平均分低,波动大 D.男生平均分低,波动小
10.已知变量x和y的统计数据如表:
x
3
4
5
6
7
y
2.5
3
4
4.5
6
根据上表可得回归直线方程y=bx–0.25,据此可以预测当x=8时,y=
A.6.4 B.6.25 C.6.55 D.6.45
11.某学校随机抽查了本校20个同学,调查他们平均每天在课外从事体育锻炼的时间(分钟),根据所得数据的茎叶图,以5为组距将数据分为八组,分别是[0,5),[5,10),…[35,40],作出的频率分布直方图如图所示,则原始的茎叶图可能是
A. B.
C. D.
12.已知变量x,y之间的线性回归方程为,且变量x,y之间的一组相关数据如表所示,则下列说法错误的是
x
6
8
10
12
y
6
m
3
2
A.变量x,y之间呈现负相关关系
B.可以预测,当x=20时,y=–3.7
C.m=4
D.由表格数据可知,该回归直线必过点(9,4)
二、填空题:请将答案填在题中横线上.
13.某地区有600家商店,其中大型商店有60家,中型商店有150家,小型商店有390家,为了掌握各商店的营业情况,要从中抽取一个容量为40的样本,若采用分层抽样的方法,抽取的中型商店数是___________.
14.某单位有842名职工,现采用系统抽样方法抽出5%的人做问卷调查,剔除适当人数后从1开始随机编号,现抽取的人中,编号落在区间[481,720]内的人数为___________.
15.对一批产品的长度(单位:毫米)进行抽样检测,样本容量为400,右图为检测结果的频率分布直方图,根据产品标准,单件产品长度在区间[25,30)的为一等品,在区间[20,25)和[30,35)的为二等品,其余均为三等品,则样本中三等品的件数为___________.
16.人甲在某周五天的时间内,每天加工零件的个数用茎叶图表示如图(左边一列的数字表示零件个数的十位数,右边的数字表示零件个数的个位数),则该组数据的方差s2的值为___________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.某体育代表队有200名运动员,其中2名是种子选手.现从中抽取13名参加运动会,要求种子选手必须参加.请采用系统抽样的方法给出抽样过程.
18.篮球运动员甲在最近6场NBA比赛中所得分数的茎叶图如图所示,由于疏忽,茎叶图中的两个数据上出现了污渍,导致这两个数字无法辨认,但统计员记得除掉污渍2处的数字不影响整体中位数,且这六个数据的平均值为17.
(1)求污渍1,2处的数字;
(2)篮球运动员乙在最近6场NBA的比赛中所得分数为8,12,16,18,20,28.试分别以各自6场比赛得分的平均数与方差来分析这两名篮球运动员的发挥水平.
19.某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:[40,50),[50,60),[60,70),…[90,100]后得到如下频率分布直方图.
(1)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的平均分、众数、中位数;(小数点后保留一位有效数字)
(2)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则[70,80)分数段抽取的人数是多少?
20.下表是某地一家超市在2014年一月份某周的时间x与每天获得的利润y(单位:万元)的有关数据.
时间x
星期二
星期三
星期四
星期五
星期六
利润y
2
3
5
6
9
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程x+;
(3)估计星期日获得的利润为多少万元.
21.某个体服装店经营某种服装在某周内获纯利y(元)与该周每天销售这件服装件数x(件)之间有如下数据:
服装件数x(件)
3
4
5
6
7
8
9
某周内获纯利y(元)
66
69
73
81
89
90
91
(1)求,;
(2)若纯利y与每天销售这件服装件数x之间是线性相关的,求回归方程;
(3)若该店每天至少要获利200元,请你预测该店每天至少要销售这种服装多少件?
22.每年的4月23日是“世界读书日”,某校研究性学习小组为了解本校学生的阅读情况,随机调查了本校200名学生在这一天的阅读时间t(单位:分钟),将样本数据整理后绘制成如图的样本频率分布直方图.
(1)求a的值;
(2)试估计该学校所有学生在这一天的平均阅读时间;
(3)若用分层抽样的方法从这200名学生中,抽出25人参加交流会,则阅读时间为[30,40),[60,70]的两组中各抽取多少人?
参考答案
1
2
3
4
5
6
7
8
9
10
11
12
B
B
A
A
C
C
C
C
A
C
B
C
1.【答案】B
【解析】据题意总体是指1901名同学的总成绩,样本是指抽取的50名同学的总成绩,个体是指每一名同学的中考数学成绩,样本容量是50,故B错误.故选B.
2.【答案】B
【解析】从表中第5行第6列开始向右读取数据,得到的前8个编号分别是:253,313,457,007,328,623,072,368.则得到的第8个样本编号是368.故选B.
3.【答案】A
【解析】由2017年第一季度五省GDP情况图,知:在A中,2017年第一季度GDP总量和增速由高到低排位均居同一位的省有江苏和山东,共2个,故A错误;在B中,与去年同期相比,2017年第一季度五个省的GDP总量均实现了增长,故B正确;在C中,去年同期河南省的GDP总量不超过4000亿元,故C正确;在D中,2017年第一季度GDP增速由高到低排位第5的是浙江省,故D正确.故选A.
6.【答案】C
【解析】根据频率分布直方图得,(0.01+a+b+0.018+0.012)×10=1,解得a+b=0.06.故选C.
7.【答案】C
【解析】从2010名学生中选取50名学生参加英语比赛,按系统抽样的方法抽取50人,由于系统抽样是一个等可能抽样,故每个人入选的概率是,故选C.
8.【答案】C
【解析】根据题意,四个参赛小队的得分为11.5,13.5,13.5,11.5;计算平均数为×(11.5+13.5+13.5+11.5)=12.5,方差为s2=×[(11.5–12.5)2+(13.5–12.5)2+(13.5–12.5)2+(11.5–12.5)2]=1.故选C.
9.【答案】A
【解析】根据茎叶图中的数据知,男同学数学成绩比较分散,且高分较多,女同学数学成绩比较集中,且低分多些,根据样本数据的数字特征知这次测验中男生平均分高些,波动大.故选A.
10.【答案】C
【解析】样本平均数=5,=4,即4=5b–0.25,∴b=0.85,∴回归直线方程y=0.85x–0.25,当x=8时,y=0.85×8–0.25=6.55,故选C.
13.【答案】10
【解析】设抽取的中型商店数为x,则,解得x=10,故答案为:10.
14.【答案】12
【解析】∵某单位有842名职工,采用系统抽样方法抽出5%的人做问卷调查,剔除适当人数后从1开始随机编号,∴抽取人数为:840×5%=42人,即从20人中抽取1人,∴现抽取的人中,编号落在区间[481,720]内的人数为:=12人.故答案为:12.
15.【答案】100
【解析】根据频率分布直方图可知,三等品的数量是[(0.0125+0.025+0.0125)×5]×400=100(件).故答案为:100.
16.【答案】
【解析】由茎叶图得该组数据的平均数为:(18+17+22+21+22)=20,∴该组数据的方差为:s2=[(18–20)2+(17–20)2+(22–20)2+(21–20)2+(22–20)2]=.故答案为:.
17.【答案】详见解析.
【解析】第一步:将除种子选手外的198名运动员随机编号为001,002,…,198;
第二步:将编号按顺序分成11段,每段18个;
第三步:在第1段001,002,…,018这18个编号中用简单随机抽样抽出一个编号(如010)作为起始号码;
第四步:将编号为010,028,046,…,190的个体抽出,与种子选手一起参加该运动会.
(2)甲的得分的平均数为x甲=17,
甲的得分的方差为
[(8–17)2+(13–17)2+(15–17)2+(24–17)2+(27–17)2]=,
乙的得分的平均数为
x乙==17.
乙的得分的方差为
[(8–17)2+(12–17)2+(16–17)2+(18–17)2+(20–17)2+(28–17)2]=,
由于x甲=x乙,,
所以两人的平均水平相当,但是乙的得分波动更小,发挥更稳定,故乙发挥水平更好.
19.【答案】(1)平均分为71、众数为75、中位数为70.3;(2)6人.
【解析】(1)根据频率和为1,列方程得:
(0.01+0.015×2+a+0.025+0.005)×10=1,解得a=0.03;
估计该校高二年级学生政治成绩的平均分为:
(45×0.01+55×0.015+65×0.015+75×0.03+85×0.025+95×0.005)×10=71;
根据频率分布直方图,估计这40名学生期中政治成绩的众数为×(70+80)=75;
因为在频率分布直方图中
第一、二、三组的频率之和为(0.010+0.015×2)×10=0.4,
所以中位数为70+≈70.3;
(2)用分层抽样法,抽取容量为20的样本,在[70,80)内抽取的人数是:
20×0.03×10=6人.
20.【答案】(1)详见解析;(2)=1.7x–1.8;(3)星期日估计获得的利润为10.1万元.
【解析】(1)由x、y的数据可得对应的散点图为
从上图可知,这些点大致分布在一条直线附近,
故时间x与获得的利润y(万元)线性相关关系显著.
(3)当x=7时,=1.7×7–1.8=10.1(万元),
所以星期日估计获得的利润为10.1万元.
21.【答案】(1)=6,=80;(2)回归方程为y=x+;(3)每天销售件数x至少为32件.
【解析】(1)(3+4+5+6+7+8+9)=6,(66+69+73+81+89+90+91)=80,
(2)3×66+4×69+5×73+6×81+7×89+8×90+9×91=3487,
32+42+52+62+72+82+92=280,
∴b=,a=,
∴回归方程为y=x+;
(3)由x+≥200,∴x≥31,
∴估计每天销售件数x至少为32件.
22.【答案】(1)a=0.032;(2)43.8分钟;(3)阅读时间在[30,40)分钟的应选8人,阅读时间在[60,70]分钟的应选3人.
【解析】(1)由已知,得0.008×10+a×10+0.012×10×2+0.036+×10=1,
解得a=0.032.
(2)由样本的频率分布直方图,估计该学校所有学生在这一天的平均阅读时间为:
(分钟).
(3)阅读时间在[30,40)分钟的人数为200×0.032×10=64,
阅读时间在[60,70]分钟的人数为200×0.012×10=24,
用分层抽样选人的抽样比为,
∴阅读时间在[30,40)分钟的应选人,
阅读时间在[60,70]分钟的应选人.
