九年级数学上册第18章 相似形 综合测试卷 (含答案)
文档属性
| 名称 | 九年级数学上册第18章 相似形 综合测试卷 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 227.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-22 19:36:19 | ||
图片预览




文档简介
北京课改版九年级数学上册
第18章相似形
综合测试卷
(时间90分钟,满分120分)
一.选择题(本大题共10小题,每小题3分,共30分)
1.下列四条线段成比例的是( )
A.a=2,b=,c=,d=2
B.a=,b=3,c=2,d=
C.a=4,b=6,c=5,d=10
D.a=2,b=8,c=15,d=11
2.已知 =,则=( )
A. B. C. D.
3.在△ABC与△A′B′C′中,有下列条件:
(1)=;(2)=;(3)∠A=∠A′;(4)∠C=∠C′.
如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A.1组 B.2组 C.3组 D.4组
4.如图,在梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )
A.2∶3 B.2∶5 C.∶ D. 4∶9
5.如图,在四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,且ED平分∠ADC,EC平分∠BCD,则下列结论中错误的有( )
A.∠ADE=∠CDE B.DE⊥EC
C.AD·BC=BE·DE D.CD=AD+BC
6. 如图,在四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,且ED平分∠ADC,EC平分∠BCD,则下列结论中错误的有( ) A.∠ADE=∠CDE B.DE⊥EC C.AD·BC=BE·DE D.CD=AD+BC
7.如图,ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
8.如图,P是△ABC的边AC上一点,连结BP,以下条件中不能判定△ABP∽△ACB的是( )
A.= B.= C.∠ABP=∠C D.∠APB=∠ABC
9.两个相似多边形的面积比是9∶16,其中较小多边形的周长为36 cm,则较大多边形的周长为( )
A.48 cm B.54 cm C.56 cm D.64 cm
10.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连结DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )
二.填空题(共8小题,3*8=24)
11.如图,△ABC中,D,E分别为AC,BC边上的点,AB∥DE,CF为AB边上的中线.若AD=5,CD=3,DE=4,则BF的长为________.
12.如图,小明在早上10时测得某树的影长为3 m,下午16时又测得该树的影长为9 m.若两次日照的光线互相垂直,则树的高度为____m.
13.如图,在平行四边形ABCD中,∠ABC的平分线BE交AD边于点E,交对角线AC于点F.若 = ,则 =____.
14.如图所示,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为( )
15.如图所示,DE与△ABC的边AB,AC分别相交于D,E两点,且DE∥BC.若DE=2 cm,BC=3 cm,EC=cm,则AC=____cm.
16.如图,小明用长为3 m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12 m,则旗杆AB的高为____m.
17.将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是______________.
18.如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①=;②FG=FB;③AF=AB;④S△ABC=5S△BDF,其中正确结论的序号是__________.
三.解答题(共9小题,66分)
19.(6分) 如图,△ACB为等腰直角三角形,点D为斜边AB上一点,连接CD,DE⊥CD,DE=CD,连接AE,过C作CO⊥AB于O.求证:△ACE∽△OCD.
20.(6分) 如图,一条小河的两岸有一段是平行的,在河的一岸每隔6 m有一棵树,在河的对岸每隔60 m有一根电线杆,在有树的一岸离岸边30 m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河的宽度.
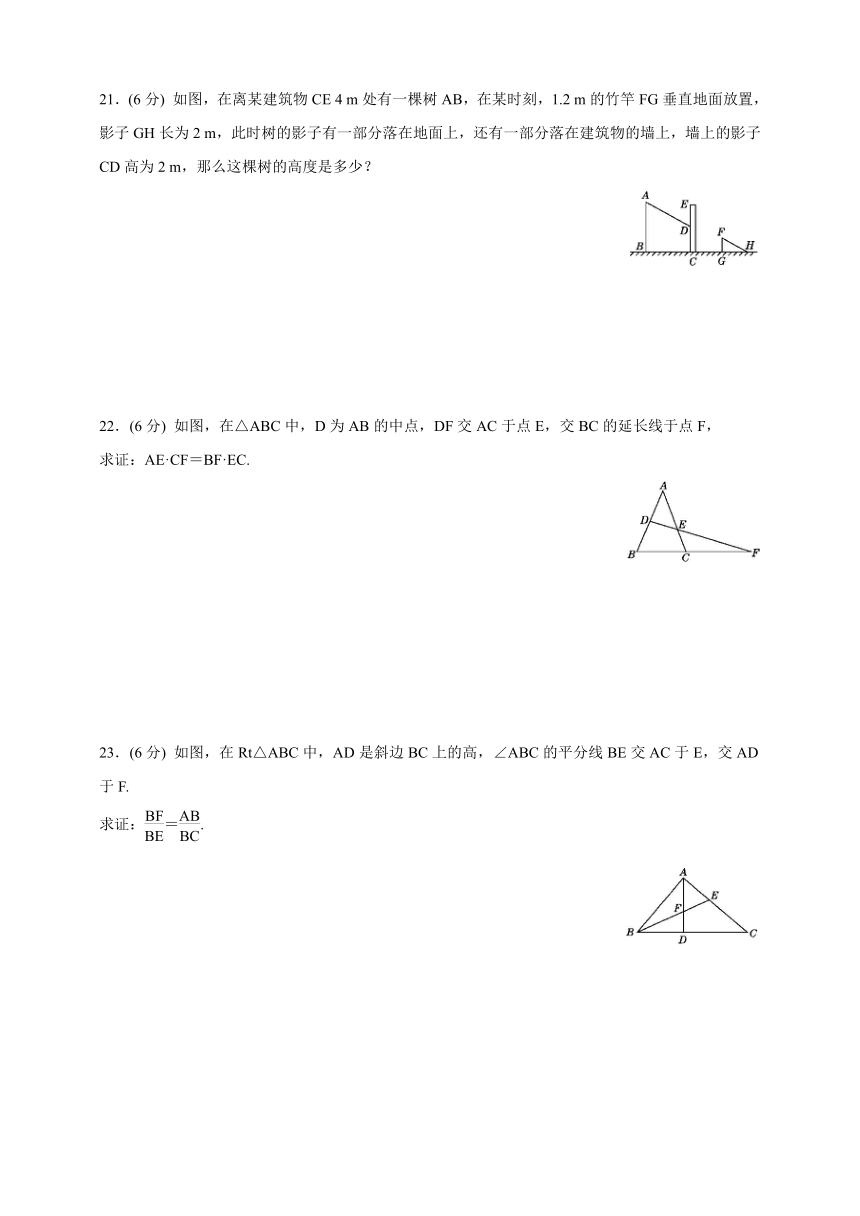
21.(6分) 如图,在离某建筑物CE 4 m处有一棵树AB,在某时刻,1.2 m的竹竿FG垂直地面放置,影子GH长为2 m,此时树的影子有一部分落在地面上,还有一部分落在建筑物的墙上,墙上的影子CD高为2 m,那么这棵树的高度是多少?
22.(6分) 如图,在△ABC中,D为AB的中点,DF交AC于点E,交BC的延长线于点F,
求证:AE·CF=BF·EC.
23.(6分) 如图,在Rt△ABC中,AD是斜边BC上的高,∠ABC的平分线BE交AC于E,交AD于F.
求证:=.
24.(8分) 如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AE·BC=BD·AC;
(2)如果S△ADE=3,S△BDE=2,DE=6,求BC的长.
25.(8分) 在△ABC中,D,E,F分别为BC,AB,AC上的点,EF∥BC,DF∥AB,连接CE和AD,分别交DF,EF于点N,M.
(1)如图①,若E为AB的中点,图中与MN平行的直线有哪几条?请证明你的结论;
(2)如图②,若E不为AB的中点,写出与MN平行的直线,并证明.
26.(10分) 如图,已知△ABC,∠BAC的平分线与∠DAC的平分线分别交BC及BC的延长线于点P,Q.
(1)求∠PAQ的度数;
(2)若点M为PQ的中点,求证:PM2=CM·BM.
27.(10分) 如图,已知矩形ABCD,AD=AB,点E,F把AB三等分,DF交AC于点G,求证:EG⊥DF.
参考答案:
1-5AACDC 6-10CBBAC
11.
12. 3
13.
14. 9
15. 2
16. 9
17. 或2
18. ①②③
19. 证明:∵△ACB为等腰直角三角形,AB为斜边,
∴∠CAB=45°.
∵CO⊥AB.∴∠AOC=90°.
又∵DE⊥CD,DE=CD,∴∠CED=45°,∠CDE=90°.
∴∠CAO=∠CED,∠AOC=∠EDC.
∴△ACO∽△ECD.∴∠ACO=∠ECD,=.
∴∠ACE=∠OCD.∴△ACE∽△OCD.
20. 解:如图,过点A作AF⊥DE,垂足为F,并延长交BC于点G.
∵DE∥BC,∴△ADE∽△ABC.
∵AF⊥DE,DE∥BC,∴AG⊥BC,∴=,∴=.
解得AG=75,∴FG=AG-AF=75-30=45,
即河的宽度为45 m.
21. 解:(方法一:作延长线)延长AD,与地面交于点M,如图①.
由AM∥FH知∠AMB=∠FHG.
又因为AB⊥BG,FG⊥BG,DC⊥BG,
所以△ABM∽△DCM∽△FGH,所以==.
因为CD=2 m,FG=1.2 m,GH=2 m,
所以=,解得CM= m.
因为BC=4 m,所以BM=BC+CM=4+=(m).
所以=,解得AB=4.4 m.
故这棵树的高度是4.4 m.
(方法二:作垂线)过点D作DM⊥AB于点M,如图②.
所以=.
而DM=BC=4 m,AM=AB-CD=AB-2(m),FG=1.2 m,GH=2 m,
所以=,解得AB=4.4 m.
故这棵树的高度是4.4 m.
22. 证明:如图,过点C作CM∥AB交DF于点M.
∵CM∥AB,∴△CMF∽△BDF.
∴=.
又∵CM∥AD,∴△ADE∽△CME.∴=.∵D为AB的中点,
∴=.∴=,即AE·CF=BF·EC.
23. 证明:易得∠BAC=∠BDF=90°.
∵BE平分∠ABC,∴∠ABE=∠DBF,
∴△BDF∽△BAE,得=.
∵∠BAC=∠BDA=90°,∠ABC=∠DBA.
∴△ABC∽△DBA,得=,∴=.
24. (1)证明:∵ED∥BC,∴△ADE∽△ABC.∴=.
∵BE平分∠ABC,∴∠DBE=∠EBC.
∵ED∥BC,∴∠DEB=∠EBC.
∴∠DBE=∠DEB.∴DE=BD.∴=,
即AE·BC=BD·AC.
(2)解:设h△ADE表示△ADE中DE边上的高,
h△BDE表示△BDE中DE边上的高,
h△ABC表示△ABC中BC边上的高.
∵S△ADE=3,S△BDE=2,∴==.
∴=.
∵△ADE∽△ABC,∴==.
∵DE=6,∴BC=10.
25. 解:(1)MN∥AC∥ED.证明如下:
∵EF∥BC,∴△AEM∽△ABD,△AMF∽△ADC,
∴==.
∵E为AB的中点,EF∥BC,∴F为AC的中点.
又∵DF∥AB,∴D为BC的中点,∴EM=MF.
∵F为AC的中点,FN∥AE,∴N为EC的中点,
从而MN∥AC.
又∵D为BC的中点,E为AB的中点,
∴ED∥AC,∴MN∥AC∥ED.
(2)MN∥AC.证明如下:∵EF∥BC,∴△AEM∽△ABD,△AMF∽△ADC,
∴==,∴=.
又∵DF∥AB,∴=,∴=,∴=.
又∵∠MEN=∠FEC,∴△MEN∽△FEC.
∴∠EMN=∠EFC.∴MN∥AC.
26. (1)解:∵AP平分∠BAC,∴∠PAC=∠BAC.
又∵AQ平分∠CAD,∴∠CAQ=∠CAD.
∴∠PAC+∠CAQ=∠BAC+∠CAD=(∠BAC+∠CAD).
又∵∠BAC+∠CAD=180°,
∴∠PAC+∠CAQ=90°,即∠PAQ=90°.
(2)证明:由(1)知∠PAQ=90°,
又∵M是线段PQ的中点,
∴PM=AM,∴∠APM=∠PAM.
∵∠APM=∠B+∠BAP,∠PAM=∠CAM+∠PAC,
∠BAP=∠PAC,
∴∠B=∠CAM.
又∵∠AMC=∠BMA,∴△ACM∽△BAM.
∴=,∴AM2=CM·BM,即PM2=CM·BM.
27. 证明:∵AD=AB,点E,F把AB三等分,
∴设AE=EF=FB=AD=k,则AB=CD=3k.
∵CD∥AB,∴∠DCG=∠FAG,∠CDG=∠AFG.
∴△AFG∽△CDG,∴==.
设FG=2m,则DG=3m,∴DF=FG+DG=2m+3m=5m.
在Rt△AFD中,DF2=AD2+AF2=5k2,∴DF=k.
∴5m=k.∴m=k.∴FG=k.
∴==,==.∴=.
又∠AFD=∠GFE,∴△AFD∽△GFE.
∴∠EGF=∠DAF=90°.∴EG⊥DF.
第18章相似形
综合测试卷
(时间90分钟,满分120分)
一.选择题(本大题共10小题,每小题3分,共30分)
1.下列四条线段成比例的是( )
A.a=2,b=,c=,d=2
B.a=,b=3,c=2,d=
C.a=4,b=6,c=5,d=10
D.a=2,b=8,c=15,d=11
2.已知 =,则=( )
A. B. C. D.
3.在△ABC与△A′B′C′中,有下列条件:
(1)=;(2)=;(3)∠A=∠A′;(4)∠C=∠C′.
如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A.1组 B.2组 C.3组 D.4组
4.如图,在梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为( )
A.2∶3 B.2∶5 C.∶ D. 4∶9
5.如图,在四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,且ED平分∠ADC,EC平分∠BCD,则下列结论中错误的有( )
A.∠ADE=∠CDE B.DE⊥EC
C.AD·BC=BE·DE D.CD=AD+BC
6. 如图,在四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,且ED平分∠ADC,EC平分∠BCD,则下列结论中错误的有( ) A.∠ADE=∠CDE B.DE⊥EC C.AD·BC=BE·DE D.CD=AD+BC
7.如图,ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个 B.2个 C.3个 D.4个
8.如图,P是△ABC的边AC上一点,连结BP,以下条件中不能判定△ABP∽△ACB的是( )
A.= B.= C.∠ABP=∠C D.∠APB=∠ABC
9.两个相似多边形的面积比是9∶16,其中较小多边形的周长为36 cm,则较大多边形的周长为( )
A.48 cm B.54 cm C.56 cm D.64 cm
10.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连结DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )
二.填空题(共8小题,3*8=24)
11.如图,△ABC中,D,E分别为AC,BC边上的点,AB∥DE,CF为AB边上的中线.若AD=5,CD=3,DE=4,则BF的长为________.
12.如图,小明在早上10时测得某树的影长为3 m,下午16时又测得该树的影长为9 m.若两次日照的光线互相垂直,则树的高度为____m.
13.如图,在平行四边形ABCD中,∠ABC的平分线BE交AD边于点E,交对角线AC于点F.若 = ,则 =____.
14.如图所示,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为( )
15.如图所示,DE与△ABC的边AB,AC分别相交于D,E两点,且DE∥BC.若DE=2 cm,BC=3 cm,EC=cm,则AC=____cm.
16.如图,小明用长为3 m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12 m,则旗杆AB的高为____m.
17.将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是______________.
18.如图,在Rt△ABC中,∠ABC=90°,BA=BC.点D是AB的中点,连结CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:①=;②FG=FB;③AF=AB;④S△ABC=5S△BDF,其中正确结论的序号是__________.
三.解答题(共9小题,66分)
19.(6分) 如图,△ACB为等腰直角三角形,点D为斜边AB上一点,连接CD,DE⊥CD,DE=CD,连接AE,过C作CO⊥AB于O.求证:△ACE∽△OCD.
20.(6分) 如图,一条小河的两岸有一段是平行的,在河的一岸每隔6 m有一棵树,在河的对岸每隔60 m有一根电线杆,在有树的一岸离岸边30 m处可看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河的宽度.
21.(6分) 如图,在离某建筑物CE 4 m处有一棵树AB,在某时刻,1.2 m的竹竿FG垂直地面放置,影子GH长为2 m,此时树的影子有一部分落在地面上,还有一部分落在建筑物的墙上,墙上的影子CD高为2 m,那么这棵树的高度是多少?
22.(6分) 如图,在△ABC中,D为AB的中点,DF交AC于点E,交BC的延长线于点F,
求证:AE·CF=BF·EC.
23.(6分) 如图,在Rt△ABC中,AD是斜边BC上的高,∠ABC的平分线BE交AC于E,交AD于F.
求证:=.
24.(8分) 如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AE·BC=BD·AC;
(2)如果S△ADE=3,S△BDE=2,DE=6,求BC的长.
25.(8分) 在△ABC中,D,E,F分别为BC,AB,AC上的点,EF∥BC,DF∥AB,连接CE和AD,分别交DF,EF于点N,M.
(1)如图①,若E为AB的中点,图中与MN平行的直线有哪几条?请证明你的结论;
(2)如图②,若E不为AB的中点,写出与MN平行的直线,并证明.
26.(10分) 如图,已知△ABC,∠BAC的平分线与∠DAC的平分线分别交BC及BC的延长线于点P,Q.
(1)求∠PAQ的度数;
(2)若点M为PQ的中点,求证:PM2=CM·BM.
27.(10分) 如图,已知矩形ABCD,AD=AB,点E,F把AB三等分,DF交AC于点G,求证:EG⊥DF.
参考答案:
1-5AACDC 6-10CBBAC
11.
12. 3
13.
14. 9
15. 2
16. 9
17. 或2
18. ①②③
19. 证明:∵△ACB为等腰直角三角形,AB为斜边,
∴∠CAB=45°.
∵CO⊥AB.∴∠AOC=90°.
又∵DE⊥CD,DE=CD,∴∠CED=45°,∠CDE=90°.
∴∠CAO=∠CED,∠AOC=∠EDC.
∴△ACO∽△ECD.∴∠ACO=∠ECD,=.
∴∠ACE=∠OCD.∴△ACE∽△OCD.
20. 解:如图,过点A作AF⊥DE,垂足为F,并延长交BC于点G.
∵DE∥BC,∴△ADE∽△ABC.
∵AF⊥DE,DE∥BC,∴AG⊥BC,∴=,∴=.
解得AG=75,∴FG=AG-AF=75-30=45,
即河的宽度为45 m.
21. 解:(方法一:作延长线)延长AD,与地面交于点M,如图①.
由AM∥FH知∠AMB=∠FHG.
又因为AB⊥BG,FG⊥BG,DC⊥BG,
所以△ABM∽△DCM∽△FGH,所以==.
因为CD=2 m,FG=1.2 m,GH=2 m,
所以=,解得CM= m.
因为BC=4 m,所以BM=BC+CM=4+=(m).
所以=,解得AB=4.4 m.
故这棵树的高度是4.4 m.
(方法二:作垂线)过点D作DM⊥AB于点M,如图②.
所以=.
而DM=BC=4 m,AM=AB-CD=AB-2(m),FG=1.2 m,GH=2 m,
所以=,解得AB=4.4 m.
故这棵树的高度是4.4 m.
22. 证明:如图,过点C作CM∥AB交DF于点M.
∵CM∥AB,∴△CMF∽△BDF.
∴=.
又∵CM∥AD,∴△ADE∽△CME.∴=.∵D为AB的中点,
∴=.∴=,即AE·CF=BF·EC.
23. 证明:易得∠BAC=∠BDF=90°.
∵BE平分∠ABC,∴∠ABE=∠DBF,
∴△BDF∽△BAE,得=.
∵∠BAC=∠BDA=90°,∠ABC=∠DBA.
∴△ABC∽△DBA,得=,∴=.
24. (1)证明:∵ED∥BC,∴△ADE∽△ABC.∴=.
∵BE平分∠ABC,∴∠DBE=∠EBC.
∵ED∥BC,∴∠DEB=∠EBC.
∴∠DBE=∠DEB.∴DE=BD.∴=,
即AE·BC=BD·AC.
(2)解:设h△ADE表示△ADE中DE边上的高,
h△BDE表示△BDE中DE边上的高,
h△ABC表示△ABC中BC边上的高.
∵S△ADE=3,S△BDE=2,∴==.
∴=.
∵△ADE∽△ABC,∴==.
∵DE=6,∴BC=10.
25. 解:(1)MN∥AC∥ED.证明如下:
∵EF∥BC,∴△AEM∽△ABD,△AMF∽△ADC,
∴==.
∵E为AB的中点,EF∥BC,∴F为AC的中点.
又∵DF∥AB,∴D为BC的中点,∴EM=MF.
∵F为AC的中点,FN∥AE,∴N为EC的中点,
从而MN∥AC.
又∵D为BC的中点,E为AB的中点,
∴ED∥AC,∴MN∥AC∥ED.
(2)MN∥AC.证明如下:∵EF∥BC,∴△AEM∽△ABD,△AMF∽△ADC,
∴==,∴=.
又∵DF∥AB,∴=,∴=,∴=.
又∵∠MEN=∠FEC,∴△MEN∽△FEC.
∴∠EMN=∠EFC.∴MN∥AC.
26. (1)解:∵AP平分∠BAC,∴∠PAC=∠BAC.
又∵AQ平分∠CAD,∴∠CAQ=∠CAD.
∴∠PAC+∠CAQ=∠BAC+∠CAD=(∠BAC+∠CAD).
又∵∠BAC+∠CAD=180°,
∴∠PAC+∠CAQ=90°,即∠PAQ=90°.
(2)证明:由(1)知∠PAQ=90°,
又∵M是线段PQ的中点,
∴PM=AM,∴∠APM=∠PAM.
∵∠APM=∠B+∠BAP,∠PAM=∠CAM+∠PAC,
∠BAP=∠PAC,
∴∠B=∠CAM.
又∵∠AMC=∠BMA,∴△ACM∽△BAM.
∴=,∴AM2=CM·BM,即PM2=CM·BM.
27. 证明:∵AD=AB,点E,F把AB三等分,
∴设AE=EF=FB=AD=k,则AB=CD=3k.
∵CD∥AB,∴∠DCG=∠FAG,∠CDG=∠AFG.
∴△AFG∽△CDG,∴==.
设FG=2m,则DG=3m,∴DF=FG+DG=2m+3m=5m.
在Rt△AFD中,DF2=AD2+AF2=5k2,∴DF=k.
∴5m=k.∴m=k.∴FG=k.
∴==,==.∴=.
又∠AFD=∠GFE,∴△AFD∽△GFE.
∴∠EGF=∠DAF=90°.∴EG⊥DF.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
