人教版数学四年级上册第六单元《应用商的变化规律进行简算》教案(表格版)
文档属性
| 名称 | 人教版数学四年级上册第六单元《应用商的变化规律进行简算》教案(表格版) |
|
|
| 格式 | zip | ||
| 文件大小 | 103.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-23 00:00:00 | ||
图片预览

文档简介
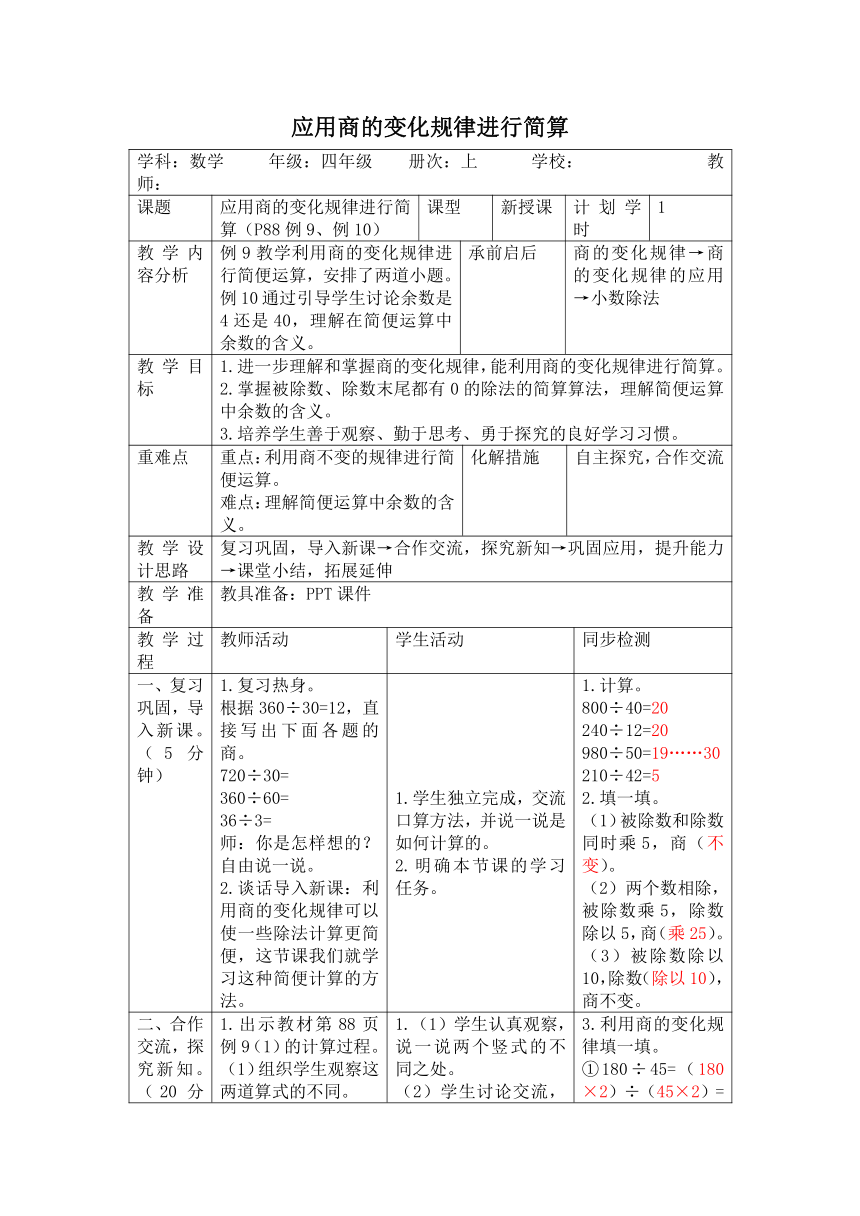
应用商的变化规律进行简算
学科:数学 年级:四年级 册次:上 学校: 教师:
课题
应用商的变化规律进行简算(P88例9、例10)
课型
新授课
计划学时
1
教学内容分析
例9教学利用商的变化规律进行简便运算,安排了两道小题。例10通过引导学生讨论余数是4还是40,理解在简便运算中余数的含义。
承前启后
商的变化规律→商的变化规律的应用→小数除法
教学目标
1.进一步理解和掌握商的变化规律,能利用商的变化规律进行简算。
2.掌握被除数、除数末尾都有0的除法的简算算法,理解简便运算中余数的含义。
3.培养学生善于观察、勤于思考、勇于探究的良好学习习惯。
重难点
重点:利用商不变的规律进行简便运算。
难点:理解简便运算中余数的含义。
化解措施
自主探究,合作交流
教学设计思路
复习巩固,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教具准备:PPT课件
教学过程
教师活动
学生活动
同步检测
一、复习巩固,导入新课。(5分钟)
1.复习热身。
根据360÷30=12,直接写出下面各题的商。
720÷30=
360÷60=
36÷3=
师:你是怎样想的?自由说一说。
2.谈话导入新课:利用商的变化规律可以使一些除法计算更简便,这节课我们就学习这种简便计算的方法。
1.学生独立完成,交流口算方法,并说一说是如何计算的。
2.明确本节课的学习任务。
1.计算。
800÷40=20
240÷12=20
980÷50=19……30
210÷42=5
2.填一填。
(1)被除数和除数同时乘5,商(不变)。
(2)两个数相除,被除数乘5,除数除以5,商(乘25)。
(3)被除数除以10,除数(除以10),商不变。
二、合作交流,探究新知。(20分钟)
1.出示教材第88页例9(1)的计算过程。
(1)组织学生观察这两道算式的不同。
(2)引导学生讨论:小英那样算对吗?
(3)组织学生汇报。
2.出示教材第88页例9(2):120÷15。
(1)让学生用竖式计算,展示计算过程。
(2)引导学生根据商不变的规律进行计算,并汇报交流。
(3)引导学生对比两种做法,说一说哪种方法更简便。
3.理解简便运算中余数的含义。
(1)出示教材第88页例10,组织学生列竖式计算。
(2)质疑:840÷50计算结果有余数,余数几?
(3)师:你能用验算的方法,验证一下余数是4,还是40吗?
(4)教师小结:利用商不变的规律计算,被除数和除数同时除以10,最终余数应该乘10,实际做题时应该注意这一问题。
1.(1)学生认真观察,说一说两个竖式的不同之处。
(2)学生讨论交流,自由发言。
(3)汇报讨论结果,明确:小英把被除数和除数同时除以10,商不变,计算正确。
2.(1)学生独立完成,展示计算过程。
(2)用商不变的规律计算,汇报交流自己的做法。
(3)在对比中明确:用“凑趣”的方法,将除数转化成整十数计算更简便。
3.(1)学生独立用竖式计算,展示计算过程。
(2)学生自由发表意见,说一说840÷50的余数是几。
(3)进行验证,汇报结果:根据“被除数=商×除数+余数”进行验证,可知:
16×50+40=840,余数是40是正确的。
16×50+4=804,不符合题意,余数不是4。
(4)认真倾听,明确利用商不变的规律计算时,余数的含义。
3.利用商的变化规律填一填。
①180÷45=(180×2)÷(45×2)=(4)。
②450÷15=(450×2)÷(15×2)=(30)。
③200÷25=(200×4)÷(25×4)=(8)。
④120÷15=(120×2)÷(15×2)=(8)。
4.在计算3200÷40时,如果除数不变,被除数乘2,那么商(乘2)。
5.你能利用商的变化规律计算下面各题吗?(P155)
4200÷300=14
3200÷30=106……20
竖式略
三、巩固应用,提升能力。(10分钟)
1.完成教材第88页“做一做”。
2.完成教材第90页“练习十七”第8题。
1.独立完成,同桌间互相检查。
2.学生独立完成,教师巡视检查。
6.算一算,填一填。
(1)35÷4=(8……3)
(2)350÷40=(8……30)
(3)3500÷400=(8……300)
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.A÷B÷C=A÷(B×C),这是除法的运算性质,你掌握了吗?做一做教材第90页第9题具体应用一下吧。
教师个人补充意见:
板书设计
培优作业
1.简便计算。
10000÷25÷4÷5÷2
=10000÷(25×4)÷(5×2)
=10000÷100÷10
=10
名师点睛
“构建合理的知识结构有利于促使小学生形成良好的认知结构”,因此应站在数学思想的高度,利用完整的“商不变的规律”把简算统整到一起,帮助学生形成稳固、可迁移的最佳认知结构。
微课设计点
教师可围绕“利用商不变的规律简算”设计微课。
学科:数学 年级:四年级 册次:上 学校: 教师:
课题
应用商的变化规律进行简算(P88例9、例10)
课型
新授课
计划学时
1
教学内容分析
例9教学利用商的变化规律进行简便运算,安排了两道小题。例10通过引导学生讨论余数是4还是40,理解在简便运算中余数的含义。
承前启后
商的变化规律→商的变化规律的应用→小数除法
教学目标
1.进一步理解和掌握商的变化规律,能利用商的变化规律进行简算。
2.掌握被除数、除数末尾都有0的除法的简算算法,理解简便运算中余数的含义。
3.培养学生善于观察、勤于思考、勇于探究的良好学习习惯。
重难点
重点:利用商不变的规律进行简便运算。
难点:理解简便运算中余数的含义。
化解措施
自主探究,合作交流
教学设计思路
复习巩固,导入新课→合作交流,探究新知→巩固应用,提升能力→课堂小结,拓展延伸
教学准备
教具准备:PPT课件
教学过程
教师活动
学生活动
同步检测
一、复习巩固,导入新课。(5分钟)
1.复习热身。
根据360÷30=12,直接写出下面各题的商。
720÷30=
360÷60=
36÷3=
师:你是怎样想的?自由说一说。
2.谈话导入新课:利用商的变化规律可以使一些除法计算更简便,这节课我们就学习这种简便计算的方法。
1.学生独立完成,交流口算方法,并说一说是如何计算的。
2.明确本节课的学习任务。
1.计算。
800÷40=20
240÷12=20
980÷50=19……30
210÷42=5
2.填一填。
(1)被除数和除数同时乘5,商(不变)。
(2)两个数相除,被除数乘5,除数除以5,商(乘25)。
(3)被除数除以10,除数(除以10),商不变。
二、合作交流,探究新知。(20分钟)
1.出示教材第88页例9(1)的计算过程。
(1)组织学生观察这两道算式的不同。
(2)引导学生讨论:小英那样算对吗?
(3)组织学生汇报。
2.出示教材第88页例9(2):120÷15。
(1)让学生用竖式计算,展示计算过程。
(2)引导学生根据商不变的规律进行计算,并汇报交流。
(3)引导学生对比两种做法,说一说哪种方法更简便。
3.理解简便运算中余数的含义。
(1)出示教材第88页例10,组织学生列竖式计算。
(2)质疑:840÷50计算结果有余数,余数几?
(3)师:你能用验算的方法,验证一下余数是4,还是40吗?
(4)教师小结:利用商不变的规律计算,被除数和除数同时除以10,最终余数应该乘10,实际做题时应该注意这一问题。
1.(1)学生认真观察,说一说两个竖式的不同之处。
(2)学生讨论交流,自由发言。
(3)汇报讨论结果,明确:小英把被除数和除数同时除以10,商不变,计算正确。
2.(1)学生独立完成,展示计算过程。
(2)用商不变的规律计算,汇报交流自己的做法。
(3)在对比中明确:用“凑趣”的方法,将除数转化成整十数计算更简便。
3.(1)学生独立用竖式计算,展示计算过程。
(2)学生自由发表意见,说一说840÷50的余数是几。
(3)进行验证,汇报结果:根据“被除数=商×除数+余数”进行验证,可知:
16×50+40=840,余数是40是正确的。
16×50+4=804,不符合题意,余数不是4。
(4)认真倾听,明确利用商不变的规律计算时,余数的含义。
3.利用商的变化规律填一填。
①180÷45=(180×2)÷(45×2)=(4)。
②450÷15=(450×2)÷(15×2)=(30)。
③200÷25=(200×4)÷(25×4)=(8)。
④120÷15=(120×2)÷(15×2)=(8)。
4.在计算3200÷40时,如果除数不变,被除数乘2,那么商(乘2)。
5.你能利用商的变化规律计算下面各题吗?(P155)
4200÷300=14
3200÷30=106……20
竖式略
三、巩固应用,提升能力。(10分钟)
1.完成教材第88页“做一做”。
2.完成教材第90页“练习十七”第8题。
1.独立完成,同桌间互相检查。
2.学生独立完成,教师巡视检查。
6.算一算,填一填。
(1)35÷4=(8……3)
(2)350÷40=(8……30)
(3)3500÷400=(8……300)
四、课堂小结,拓展延伸。(5分钟)
1.这节课我们学习了什么?引导学生回顾总结。
2.A÷B÷C=A÷(B×C),这是除法的运算性质,你掌握了吗?做一做教材第90页第9题具体应用一下吧。
教师个人补充意见:
板书设计
培优作业
1.简便计算。
10000÷25÷4÷5÷2
=10000÷(25×4)÷(5×2)
=10000÷100÷10
=10
名师点睛
“构建合理的知识结构有利于促使小学生形成良好的认知结构”,因此应站在数学思想的高度,利用完整的“商不变的规律”把简算统整到一起,帮助学生形成稳固、可迁移的最佳认知结构。
微课设计点
教师可围绕“利用商不变的规律简算”设计微课。
