江苏扬州高邮市2020届高三上学期9月学情调研考试 数学(文) (Word版)
文档属性
| 名称 | 江苏扬州高邮市2020届高三上学期9月学情调研考试 数学(文) (Word版) |

|
|
| 格式 | zip | ||
| 文件大小 | 214.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-24 00:00:00 | ||
图片预览



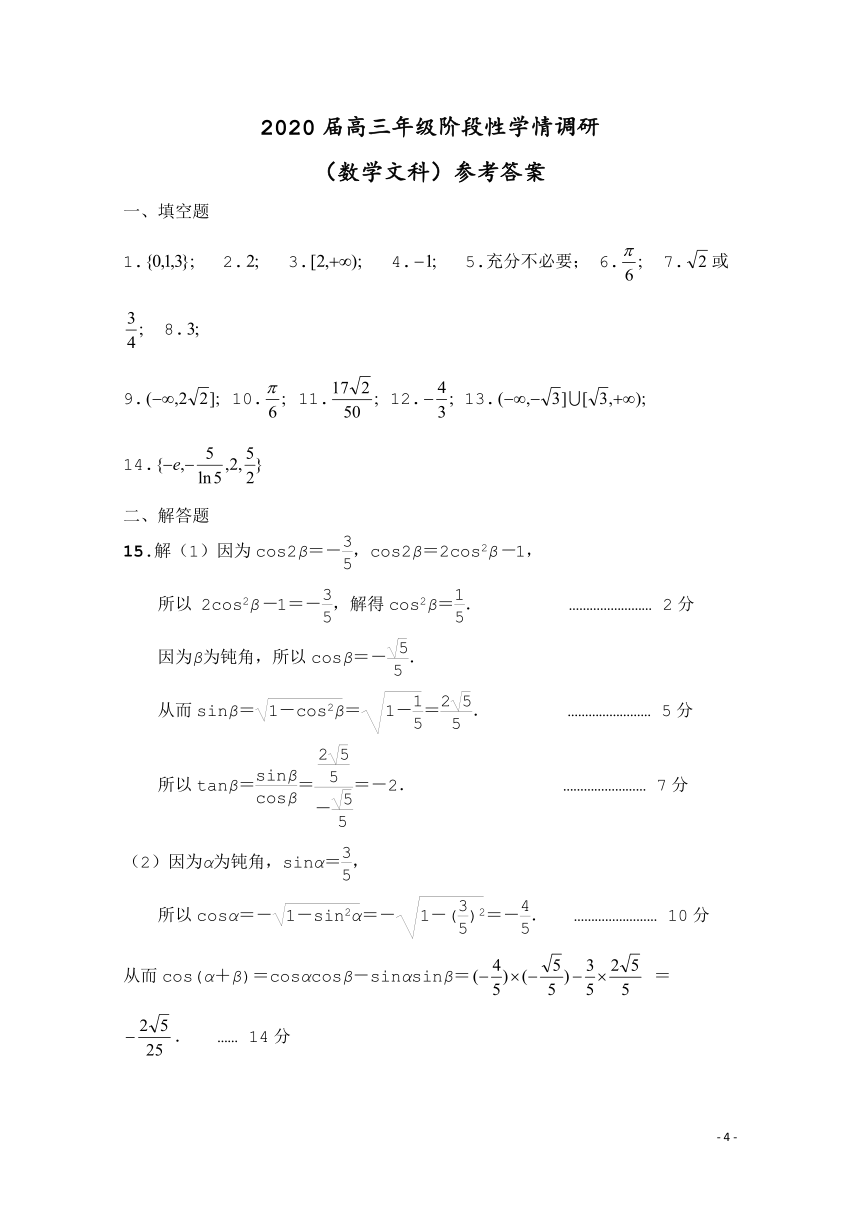
文档简介
江苏扬州高邮市2020届高三年级阶段性学情调研
数学(文科)试题 2019.09
考试时间:120分钟 总分:160分
一、填空题(本大题共14小题,每小题5分,共计70分。请把答案填写在答题卡相应位置上)
1.已知集合A= {-1,0,1,3},B = { },则▲ .
2.己知复数的实部为0,其中i为虚数单位,则实数a的值是 ▲ .
3.函数的定义域为 ▲ .
4.已知直线和平行,则实数 a 的值为 ▲ .
5.设命题;命题,那么是的▲条件.(选填“充分不必要”、 “必要不充分”、“充要”、“既不充分也不必要”)
6.在中,角A,B,C的对边分别为a,b,c, ,则B= .
7.已知函数,若,则实数▲.
8.设曲线的图象在点(1,)处的切线斜率为2,则实数的值为 ▲
9.若“,使得成立”是假命题,则实数的取值范围是 ▲.
10.在平面直角坐标系中,将函数的图象向右平移个单位长度后,得到的图象经过坐标原点,则的值为 ▲.
11.已知,则的值为
12.如图,在中,AB=BC,BC=2, ,若,则
13.在平面直角坐标系中,己知直线与曲线从左至右依次交于A、B、C三点,若直线上存在点P,满足,则实数的取值范围为
14.已知函数,若,若关于的方程恰有三个不同的实数解,则满足条件的所有实数的取值集合为 ▲ .
二、解答题(本大题共6小题,共计90分.解答时应写出文字说明、证明过程或演算步骤)
15.(本题满分14分)
己知为钝角,且.
(1)求的值:
(2)求的值.
16.(本题满分14分)
已知.
(1)求与的夹角;
(2)求;
(3)若,求实数的值.
17.(本题满分15分)
在中,a,b,c 分别为角 A, B, C 所对边的长,.
(1)求角C的值;
(2)设函数,求的取值范围.
18. (本题满分15分)
在平面直角坐标系中,己知圆C: ,且圆C被直线截得的弦长为2.
(1)求圆C的标准方程;
(2)若圆C的切线在轴和轴上的截距相等,求切线的方程;
(3)若圆D: 上存在点P,由点P向圆C引一条切线,切点为M,且满足,求实数的取值范围.
19.(本题满分16分)
如图,在P地正西方向16cm的A处和正东方向2km的B处各一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F.
(1)若在P处看E,F的视角,在B处看E测得,求AE,BF;
(2)为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设,公路PF的每千米建设成本为a万元,公路PE的每千米建设成本为8a万元.为节省建设成本,试确定E,F的位置,使公路的总建设成本最小.
20.(本题满分16分)
已知函数在处的切线方程为 ,函数.
(1)求函数的解析式;
(2)求函数的极值;
(3)设表示中的最小值),若在上恰有三个零点,求实数的取值范围.
2020届高三年级阶段性学情调研
(数学文科)参考答案
填空题
1. 2. 3. 4. 5.充分不必要; 6. 7.或 8.
9. 10. 11. 12. 13. 14.
二、解答题
15.解(1)因为cos2β=-,cos2β=2cos2β-1,
所以 2cos2β-1=-,解得cos2β=. …………………… 2分
因为β为钝角,所以cosβ=-.
从而sinβ===. …………………… 5分
所以tanβ===-2. …………………… 7分
(2)因为α为钝角,sinα=,
所以cosα=-=-=-. …………………… 10分
从而cos(α+β)=cosαcosβ-sinαsinβ= =. …… 14分
16.解:由题意得
17.解:(1)在△ABC中, 因为,
由正弦定理,
所以. …… 3分
即,
由余弦定理,得. …… 5分
又因为,所以. …… 7分
因为=
= …… 10分
由(1)可知,且在△ABC中,
所以,即 …… 12分
所以,即
所以的取值范围为 …… 15分
解:(1)由题意得
(2)因为直线在x轴和y轴上的截距相等,
①若直线过原点,则假设直线的方程为,因为直线与圆C相切,
②若直线不过原点,切线l在x轴和y轴上的截距相等,则假设直线的方程为因为相切,
19.解:(1) 在中,由题意可知,则.……2分
在中,,在中 4分 因为所以 于是
所以………6分
答:……7分
由公路的成本为公路的成本的倍,所以最小时公路的建设成本最小.
在Rt△PAE中,由题意可知,则.
同理在Rt△PBF中,,则.
令,………………………………9分
则…………………………11分
令,得,记,,
当时,,单调减;
当时,,单调增.
所以时,取得最小值, …………………………………13分
此时,.…………………………15分
所以当AE为4km,且BF为8km时,成本最小. ……………………16分
解:(1)
因为在处的切线方程为
所以, ………………2分
解得 所以 ……………3分
(2)的定义域为
①若时,则在上恒成立,
所以在上单调递增,无极值 …………5分
②若时,则
当时,,在上单调递减;
当时,,在上单调递增;
所以当时,有极小值,无极大值.……7分
(3)因为仅有一个零点1,且恒成立,所以在上有仅两个不等于1的零点. ……8分
①当时,由(2)知, 在上单调递增,在上至多一个零点,不合题意,舍去
②当时,,在无零点
③当时,,当且仅当等号成立,在仅一个零点11分
④当时,,,所以,
又图象不间断,在上单调递减
故存在,使 …………13分
又 下面证明,当时,
>0, 在上单调递增
所以
又图象在上不间断,在上单调递增,
故存在,使 …………15分
综上可知,满足题意的的范围是 ……16分
(注:取亦可)
数学(文科)试题 2019.09
考试时间:120分钟 总分:160分
一、填空题(本大题共14小题,每小题5分,共计70分。请把答案填写在答题卡相应位置上)
1.已知集合A= {-1,0,1,3},B = { },则▲ .
2.己知复数的实部为0,其中i为虚数单位,则实数a的值是 ▲ .
3.函数的定义域为 ▲ .
4.已知直线和平行,则实数 a 的值为 ▲ .
5.设命题;命题,那么是的▲条件.(选填“充分不必要”、 “必要不充分”、“充要”、“既不充分也不必要”)
6.在中,角A,B,C的对边分别为a,b,c, ,则B= .
7.已知函数,若,则实数▲.
8.设曲线的图象在点(1,)处的切线斜率为2,则实数的值为 ▲
9.若“,使得成立”是假命题,则实数的取值范围是 ▲.
10.在平面直角坐标系中,将函数的图象向右平移个单位长度后,得到的图象经过坐标原点,则的值为 ▲.
11.已知,则的值为
12.如图,在中,AB=BC,BC=2, ,若,则
13.在平面直角坐标系中,己知直线与曲线从左至右依次交于A、B、C三点,若直线上存在点P,满足,则实数的取值范围为
14.已知函数,若,若关于的方程恰有三个不同的实数解,则满足条件的所有实数的取值集合为 ▲ .
二、解答题(本大题共6小题,共计90分.解答时应写出文字说明、证明过程或演算步骤)
15.(本题满分14分)
己知为钝角,且.
(1)求的值:
(2)求的值.
16.(本题满分14分)
已知.
(1)求与的夹角;
(2)求;
(3)若,求实数的值.
17.(本题满分15分)
在中,a,b,c 分别为角 A, B, C 所对边的长,.
(1)求角C的值;
(2)设函数,求的取值范围.
18. (本题满分15分)
在平面直角坐标系中,己知圆C: ,且圆C被直线截得的弦长为2.
(1)求圆C的标准方程;
(2)若圆C的切线在轴和轴上的截距相等,求切线的方程;
(3)若圆D: 上存在点P,由点P向圆C引一条切线,切点为M,且满足,求实数的取值范围.
19.(本题满分16分)
如图,在P地正西方向16cm的A处和正东方向2km的B处各一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F.
(1)若在P处看E,F的视角,在B处看E测得,求AE,BF;
(2)为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设,公路PF的每千米建设成本为a万元,公路PE的每千米建设成本为8a万元.为节省建设成本,试确定E,F的位置,使公路的总建设成本最小.
20.(本题满分16分)
已知函数在处的切线方程为 ,函数.
(1)求函数的解析式;
(2)求函数的极值;
(3)设表示中的最小值),若在上恰有三个零点,求实数的取值范围.
2020届高三年级阶段性学情调研
(数学文科)参考答案
填空题
1. 2. 3. 4. 5.充分不必要; 6. 7.或 8.
9. 10. 11. 12. 13. 14.
二、解答题
15.解(1)因为cos2β=-,cos2β=2cos2β-1,
所以 2cos2β-1=-,解得cos2β=. …………………… 2分
因为β为钝角,所以cosβ=-.
从而sinβ===. …………………… 5分
所以tanβ===-2. …………………… 7分
(2)因为α为钝角,sinα=,
所以cosα=-=-=-. …………………… 10分
从而cos(α+β)=cosαcosβ-sinαsinβ= =. …… 14分
16.解:由题意得
17.解:(1)在△ABC中, 因为,
由正弦定理,
所以. …… 3分
即,
由余弦定理,得. …… 5分
又因为,所以. …… 7分
因为=
= …… 10分
由(1)可知,且在△ABC中,
所以,即 …… 12分
所以,即
所以的取值范围为 …… 15分
解:(1)由题意得
(2)因为直线在x轴和y轴上的截距相等,
①若直线过原点,则假设直线的方程为,因为直线与圆C相切,
②若直线不过原点,切线l在x轴和y轴上的截距相等,则假设直线的方程为因为相切,
19.解:(1) 在中,由题意可知,则.……2分
在中,,在中 4分 因为所以 于是
所以………6分
答:……7分
由公路的成本为公路的成本的倍,所以最小时公路的建设成本最小.
在Rt△PAE中,由题意可知,则.
同理在Rt△PBF中,,则.
令,………………………………9分
则…………………………11分
令,得,记,,
当时,,单调减;
当时,,单调增.
所以时,取得最小值, …………………………………13分
此时,.…………………………15分
所以当AE为4km,且BF为8km时,成本最小. ……………………16分
解:(1)
因为在处的切线方程为
所以, ………………2分
解得 所以 ……………3分
(2)的定义域为
①若时,则在上恒成立,
所以在上单调递增,无极值 …………5分
②若时,则
当时,,在上单调递减;
当时,,在上单调递增;
所以当时,有极小值,无极大值.……7分
(3)因为仅有一个零点1,且恒成立,所以在上有仅两个不等于1的零点. ……8分
①当时,由(2)知, 在上单调递增,在上至多一个零点,不合题意,舍去
②当时,,在无零点
③当时,,当且仅当等号成立,在仅一个零点11分
④当时,,,所以,
又图象不间断,在上单调递减
故存在,使 …………13分
又 下面证明,当时,
>0, 在上单调递增
所以
又图象在上不间断,在上单调递增,
故存在,使 …………15分
综上可知,满足题意的的范围是 ……16分
(注:取亦可)
同课章节目录
