12.2一次函数图像与性质专题练习(含答案解析)
文档属性
| 名称 | 12.2一次函数图像与性质专题练习(含答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 931.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-23 12:22:44 | ||
图片预览

文档简介
一次函数图像与性质专题
考试范围:12.2;考试时间:120分钟;
一、单选题(每题4分,共20分))
1.已知(2、3)在函数的图象上,那么下列各点中在此函数图象上的是 ( )
A.(-2,-3) B.( -2,3) C.(3,-2) D.(-3,-2)
2.下列各式是一次函数的是( )
A. B. C. D.
3.若函数的图象过,则关于此函数的叙述不正确的是( )
A.y随x的增大而增大 B.
C.函数图象经过原点 D.函数图象过二、四象限
4.已知正比例函数,且随的增大而减小,则的取值范围是( )
A. B. C. D.
5.把直线向下平移3个单位长度得到直线为( )
A. B. C. D.
6.已知、是一次函数图象上的两个点,则与的大小关系为( )
A. B. C. D.不能确定与的大小
7.一次函数y=kx+k的图象可能是( )
A. B.
C. D.
8.如图,已知一次函数y=kx+b(k,b为常数,且k≠0)的图象与x轴交于点A(3,0),若正比例函数y=mx(m为常数,且m≠0)的图象与一次函数的图象相交于点P,且点P的横坐标为1,则关于x的不等式(k-m)x+b<0的解集为( )
A. B. C. D.
9.已知函数的图象经过原点,则的值为( )
A. B. C. D.
10.甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二、填空题
11.直线,在轴上的截距是________.
12.正方形,,,...按如图的方式放置,点,,...和点,,...分别在直线和轴上,则点的坐标为_______.
13.一个有进水管与出水管的容器,从某时刻开始内只进水不出水,在随后的内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量单位:)与时间(单位)之间的关系如图所示:则时容器内的水量为__________.
14.一次函数图象过点日与直线平行,则一次函数解析式__________.
三、解答题
15.如图,点A、B、C的坐标分别为(﹣3,1)、(﹣4,﹣1)、(﹣1,﹣1),将△ABC先向下平移2个单位,得△A1B1C1;再将△A1B1C1沿y轴翻折180°,得△A2B2C2;.
(1)画出△A1B1C1和△A2B2C2;
(2)求直线A2A的解析式.
16.已知某市2018年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图.
(1)当x≥50时,求y关于x的函数关系式;
(2)若某企业2018年10月份的水费为620元,求该企业2018年10月份的用水量.
17.“黄金1号”玉米种子的价格为5元/kg,如果一次购买2kg以上的种子,超过2kg部分的种子的价格打8折.
(1)根据题意,填写下表:
购买种子的数量/kg 1.5 2 3.5 4 …
付款金额/元 7.5 16 …
(2)设购买种子数量为xkg,付款金额为y元,求y关于x的函数解析式;
(3)若小张一次购买该种子花费了30元,求他购买种子的数量.
18.有一种节能型轿车的油箱加满天然气后,油箱中的剩余天然气量(升)与轿车行驶路程(千米)之间的关系如图所示,根据图象回答下列问题:
(1)这种轿车的油箱最多能装______升天然气,加满天然气后可供轿车行驶______千米.
(2)轿车每行驶200千米消耗天然气________升.
(3)写出与之间的函数关系式.
19.已知一次函数的图像经过点, .
(1)求一次函数的表达式.
(2)在所给直角坐标系中画出此函数的图像.
(3)求直线与两坐标轴所围成的三角形面积.
(4)根据图像回答:当__________时, .
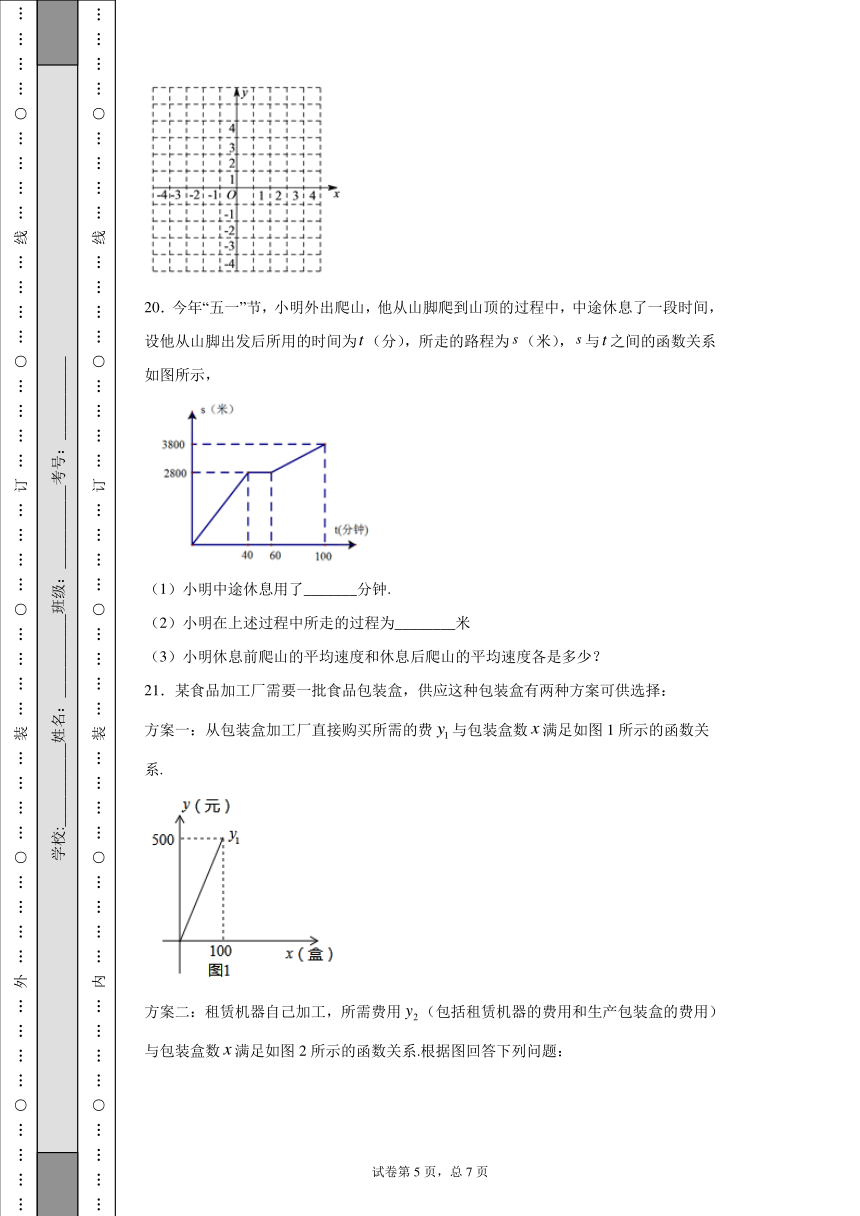
20.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间,设他从山脚出发后所用的时间为(分),所走的路程为(米),与之间的函数关系如图所示,
(1)小明中途休息用了_______分钟.
(2)小明在上述过程中所走的过程为________米
(3)小明休息前爬山的平均速度和休息后爬山的平均速度各是多少?
21.某食品加工厂需要一批食品包装盒,供应这种包装盒有两种方案可供选择:
方案一:从包装盒加工厂直接购买所需的费与包装盒数满足如图1所示的函数关系.
方案二:租赁机器自己加工,所需费用(包括租赁机器的费用和生产包装盒的费用)与包装盒数满足如图2所示的函数关系.根据图回答下列问题:
(1)方案一中每个包装盒的价格是多少元?
(2)方案二中租赁机器的费用是多少元?生产一个包装盒的费用是多少元?
(3)请分别求出y1、y2与x的函数关系式,如果你是决策者,你认为应该选择哪种方案更省钱?并说明理由.
22.如图,直线的解析式为,且与轴交于点D,直线经过点、,直线、交于点C.
(1)求直线的解析表达式;
(2)求的面积;
(3)在直线上存在异于点C的另一点P,使得与的面积相等,请求出点P的坐标.
23.阅读下列一段文字,然后回答下列问题.
已知在平面内有两点、,其两点间的距离,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为或.
(1)已知、,试求A、B两点间的距离______.
已知M、N在平行于y轴的直线上,点M的纵坐标为4,点N的纵坐标为-1,试求M、N两点的距离为______;
(2)已知一个三角形各顶点坐标为、、,你能判定此三角形的形状吗?说明理由.
(3)在(2)的条件下,平面直角坐标系中,在x轴上找一点P,使的长度最短,求出点P的坐标及的最短长度.
参考答案
1.A
【解析】
【分析】
由点在直线上可得出关于k的一元一次方程,解方程即可得出k的值,从而得出正比例函数的解析式,再将4个选项中点的坐标分别代入一次函数解析式去验证点是否在直线上,由此即可得出结论.
【详解】
解:∵点(2,3)在函数y=kx(k≠0)的图象上,
∴3=2k,解得:k=,
∴正比例函数解析式为y=x.
A. (-2,-3), ×(-2)=-3 ,-3 = -3,A中的点在直线上;
B. ( -2,3), ×(-2)=-3 ,-3≠3,B中的点不在直线上;
C. (3,-2), ×3=≠-2, C中的点不在直线上;
D. (-3,-2),×(-3)= -≠-2, D中的点不在直线上.
故选:A.
【点睛】
本题考查了正比例函数图象上点的坐标特征,解题的关键是得出正比例函数解析式.本题属于基础题,难度不大,解决该题型题目时,根据点在直线上得出方程(或方程组)是关键.
2.B
【解析】
【分析】
依据一次函数的定义进行解答即可.
【详解】
A、是二次函数反比例函数,故A错误;
B、是一次函数,故B正确;
C、不是一次函数,故C错误;
D、是反比例函数,故D错误.
故选:B.
【点睛】
本题主要考查的是一次函数的定义,掌握一次函数的定义是解题的关键.
3.A
【解析】
【分析】
将(2,-3)代入一次函数解析式中,求出一次函数解析式,根据解析式得出一次函数图像与性质即可得出答案.
【详解】
将(2,-3)代入中
2k=-3,解得
∴一次函数的解析式为:
A:根据解析式可得y随x的增大而减小,故A选项正确;
B:,故B选项错误;
C:为正比例函数,图像经过原点,故C选项错误;
D:根据解析式可得函数图像经过二、四象限,故D选项错误.
故答案选择A.
【点睛】
本题考查了用待定系数法求一次函数解析式以及根据一次函数解析式判断函数的图像与性质.
4.D
【解析】
【分析】
根据正比例函数的性质,时,随的增大而减小,即,即可得解.
【详解】
根据题意,得
即
故答案为D.
【点睛】
此题主要考查正比例函数的性质,熟练掌握,即可解题.
5.D
【解析】
【分析】
根据直线平移的性质,即可得解.
【详解】
根据题意,得
故答案为D.
【点睛】
此题主要考查一次函数的平移,熟练掌握,即可解题.
6.C
【解析】
【分析】
先根据一次函数中k=-2判断出函数的增减性,再根据-3<2进行解答即可.
【详解】
解:∵一次函数中k=-2<0,
∴y随x的增大而减小,
∵-3<2,
∴y1>y2.
故选:C.
【点睛】
本题考查一次函数图象上点的坐标特点及一次函数的性质,熟知一次函数的增减性是解题的关键.
7.B
【解析】
试题分析:根据一次函数的图象与系数的关系进行解答即可.
解:当k>0时,函数图象经过一、二、三象限;
当k<0时,函数图象经过二、三、四象限,故B正确.
故选B.
8.B
【解析】
【分析】
根据函数图像分析即可解题.
【详解】
由函数图像可知一次函数单调递减,正比例函数单调递增,
将(k-m)x+b<0变形,即kx+b<mx,
对应图像意义为一次函数图像在正比例函数图像下方,即交点P的右侧,
∵点P的横坐标为1,
∴即为所求解集.故选:B
【点睛】
本题考查了一次函数与正比例函数的图像问题,数形结合的解题方法,中等难度, 将不等式问题转化为图像问题是解题关键,
9.B
【解析】
【分析】
根据已知条件知,关于x的一次函数y=2x+m-1的图象经过点(0,0),所以把(0,0)代入已知函数解析式列出关于系数m的方程,通过解方程即可求得m的值.
【详解】
解:∵关于x的一次函数y=2x+m-1的图象经过原点,
∴点(0,0)满足一次函数的解析式y=2x+m-1,
∴0=m-1,
解得m=1.
故选:B.
【点睛】
本题考查一次函数图象上点的坐标特点,熟知一次函数y=kx+b(k≠0)中,当b=0时函数图象经过原点是解题的关键.
10.A
【解析】
【分析】
根据乙追上甲的时间求出乙的速度可判断①,根据乙由相遇点到达B点所用时间可确定m的值,即可判断②,根据乙休息1h甲所行驶的路程可判断③,由乙返回时,甲乙相距80km,可求出两车相遇的时间即可判断④.
【详解】
由图象可知,乙出发时,甲乙相距80km,2小时后,乙车追上甲.则说明乙每小时比甲快40km,则乙的速度为120km/h.①正确;
由图象第2﹣6小时,乙由相遇点到达B,用时4小时,每小时比甲快40km,则此时甲乙距离4×40=160km,则m=160,②正确;
当乙在B休息1h时,甲前进80km,则H点坐标为(7,80),③正确;
乙返回时,甲乙相距80km,到两车相遇用时80÷(120+80)=0.4小时,则n=6+1+0.4=7.4,④错误.
所以正确的有①②③,
故选A.
【点睛】
本题考查通过分段函数图像解决问题,根据题意明确图像中的信息是解题关键.
11.-10
【解析】
【分析】
令x=0解得y值,即为直线在y轴上的截距.
【详解】
,
令x=0,解得y=-10,
即直线在轴上的截距是-10.
故答案为:-10
【点睛】
此题考查直线在坐标轴上的截距,掌握定义是解答此题的关键.
12.
【解析】
【分析】
按照由特殊到一般的思路,先求出点A 1、B 1;A 2、B 2;A 3、B 3;A 4、B 4的坐标,得出一般规律,进而得出点A n、Bn的坐标,代入即得答案.
【详解】
解:∵直线,x=0时,y=1,∴OA 1=1,
∴点A 1的坐标为(0,1),点B 1的坐标为(1,1),
∵对直线,当x=1时,y=2,∴A 2C 1=2,
∴点A 2的坐标为(1,2),点B 2的坐标为(3,2),
∵对直线,当x=3时,y=4,∴A 3C 2=4,
∴点A 3的坐标为(3,4),点B 3的坐标为(7,4),
∵对直线,当x=7时,y=8,∴A 4C 3=8,
∴点A 4的坐标为(7,8),点B 4的坐标为(15,8),
……
∴点A n的坐标为(2 n ﹣1﹣1,2 n ﹣1), 点B n的坐标为(2 n ﹣1,2 n ﹣1)
∴点的坐标为(2 2019 ﹣1,2 2018)
【点睛】
本题主要考查一次函数图象上点的坐标特征、正方形的性质和规律的探求,解决这类问题一般从特殊情况入手,找出数量上的变化规律,从而推出一般性的结论.
13.25
【解析】
【分析】
利用待定系数法求后8分钟的解析式,再求函数值.
【详解】
解:根据题意知:后8分钟水量y(单位:L)与时间x(单位:min)之间的关系满足一次函数关系,设y=kx+b
?当x=4,y=20
?当x=12,y=30
∴
∴
∴后8分钟水量y(单位:L)与时间x(单位:min)之间的关系满足一次函数关系y=1.25x+15
?当x=8时,y=25.
故答案为:25.
【点睛】
本题考查利用待定系数法求一次函数解析式,并根据自变量取值,再求函数值.求出解析式是解题关键.
14.
【解析】
【分析】
设一次函数解析式为y=kx+b,先把(0,-2)代入得b=-2,再利用两直线平行的问题得到k=-3,即可得到一次函数解析式.
【详解】
解:设一次函数解析式为y=kx+b,
把(0,-2)代入得b=-2,
∵直线y=kx+b与直线y=2-3x平行,
∴k=-3,
∴一次函数解析式为y=-3x-2.
故答案为:y=-3x-2.
【点睛】
本题考查两直线相交或平行的问题:若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.
15.(1)见解析;(2)
【解析】分析:(1)将△ABC的三个顶点分别向下平移2个单位,得到新的对应点,顺次连接得△A1B1C1;再从△A1B1C1三个顶点向y轴引垂线并延长相同单位,得到新的对应点,顺次连接,得△A2B2C2;
(2)设直线A2A的解析式为y=kx+b,再把点A(﹣3,1),A2(3,﹣1)代入,用待定系数法求出它的解析式.
详解:(1)如图所示:△A1B1C1,△A2B2C2即为所求;
(2)设直线A2A的解析式为y=kx+b
把点的坐标A(﹣3,1)A2的坐标(3,﹣1)代入上式得:
,
解得:,
所以直线A2A的解析式为.
点睛:本题考查了平移作图,轴对称作图,待定系数法求一次函数解析式,熟练掌握待定系数法求函数关系式是解答本题的关键.
16.(1)y=6x﹣100;(2)120吨
【解析】
【分析】
(1)设y关于x的函数关系式y=kx+b,然后利用待定系数法求一次函数解析式解答;
(2)把水费620元代入函数关系式解方程即可.
【详解】
(1)设y关于x的函数关系式y=kx+b,则:
解得:,所以,y关于x的函数关系式是y=6x﹣100;
(2)由图可知,当y=620时,x>50,所以,6x﹣100=620,解得:x=120.
答:该企业2018年10月份的用水量为120吨.
【点睛】
本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,已知函数值求自变量.
17.(Ⅰ)10,18;(Ⅱ)见解析;(Ⅲ)他购买种子的数量是7千克.
【解析】
试题分析:(1)根据单价乘以数量,可得答案;
(2)根据单价乘以数量,可得价格,可得相应的函数解析式;
(3)根据函数值,可得相应的自变量的值.
试题解析:(1)10;18
(2)根据题意,知当0≤x≤2时,种子的价格为5元/kg,
所以y=5x;
当x>2时,其中有2 kg的种子按5元/kg付款,其余的(x-2)kg种子按4元/kg(即8折)付款.
所以y=5×2+4(x-2)=4x+2.
所以y关于x的函数表达式为y= ;
(3)因为30>10,所以他一次购买种子的数量超过2 kg.
令30=4x+2,解得x=7.
答:他购买种子的数量是7 kg.
18.(1)50,1000;(2)轿车每行驶200千米消耗天然气10升;(3)
【解析】
【分析】
(1)观察图形,即可求得这种轿车的油箱最多能装多少升天然气及一箱天然气可供轿车行驶多少千米;
(2)根据一种节能型轿车的邮箱最多可装天然气50升,可以行驶1000km,可求行驶1km需要天然气的升数,即可得出每行驶200千米消耗汽油升数;
(3)根据剩余油量=节能型轿车的油箱容量-每100千米消耗油量×行驶里程,利建立函数关系式用待定系数法求解.
【详解】
(1)50,1000
(2)200×(50÷1000)=10(升).
答:轿车每行驶200千米消耗天然气10升.
(3)设与之间的关系式为,代入(0,50),(1000,0)得:
解得:
故与之间的关系式为()
【点睛】
此题主要考查了一次函数的应用以及待定系数法求一次函数解析式,从一次函数的图象上获取正确的信息是解题关键.
19.();()图象见解析;(3)4;(4)<2.
【解析】试题分析:(1)将两点代入,运用待定系数法求解;
(2)两点法即可确定函数的图象;
(3)求出与x轴及y轴的交点坐标,然后根据面积公式求解即可;
(4)观察图象即可得.
试题解析:()将, 和, 代入得,
,
解得: , ,
∴;
()如图所示:
(3)直线y=-2x+4交x轴于点(2,0),所以S= =4;
(4)由图可知,当时, .
20.(1)20;(2)3800;(3)小明休息前爬山的平均速度是70米/分,休息后爬山的平均速度是25米/分.
【解析】
【分析】
(1)从图像来看,小明在第40分钟时开始休息,第60分钟时结束休息,故休息用了20分钟;
(2)根据图像可得小明所走的路程为3800米;
(3)根据图像信息,即可求得小明休息前和休息后爬山的平均速度.
【详解】
(1)根据图像信息,可得
小明在第40分钟时开始休息,第60分钟时结束休息,故中途休息用了20分钟;
(2)根据图像,得
小明所走的路程为3800米;
(3)根据图像,得
小明休息前爬山的平均速度是米/分,
小明休息后爬山的平均速度是米/分.
【点睛】
此题主要考查一次函数的实际应用,熟练掌握,即可解题.
21.(1)方案一的盒子单价为5元;(2)租赁机器的费用为20000元,盒子的单价为2.5元;(3)当时,两种方案同样省钱;当时,选择方案一;当时,选择方案二.
【解析】
【分析】
(1)根据图象1可知100个盒子共花费500元,据此可以求出盒子的单价;
(2)根据图2可以知道租赁机器花费20000元,根据图象所经过的点的坐标求出盒子的单价即可;
(3)根据图象经过的点的坐标用待定系数法求得函数的解析式即可;求出当x的值为多少时,两种方案同样省钱,并据此分类讨论最省钱的方案即可.
【详解】
(1)500÷100=5,
∴方案一的盒子单价为5元;
(2)根据函数的图象可以知道租赁机器的费用为20000元,
盒子的单价为(30000-20000)÷4000=2.5,
故盒子的单价为2.5元;
(3)设图象一的函数解析式为:,
由图像知函数经过点,
∴,
解得,
∴函数的解析式为;
设图像二的函数关系式为
由图像知道函数的图像经过点和
∴,
解得:,
∴函数的解析式为,
解得,
∴当时,两种方案同样省钱;
当时,选择方案一;
当时,选择方案二.
【点睛】
本题考查了一次函数的应用,解题的关键是从实际问题中整理出函数模型,并利用函数的知识解决实际问题.
22.(1);(2);(3)P(6,3).
【解析】
试题分析:(1)利用待定系数法求直线的解析表达式;
(2)由方程组得到C(2,﹣3),再利用x轴上点的坐标特征确定D点坐标,然后根据三角形面积公式求解;
(3)由于△ADP与△ADC的面积相等,根据三角形面积公式得到点D与点C到AD的距离相等,则D点的纵坐标为3,对于函数,计算出函数值为3所对应的自变量的值即可得到D点坐标.
试题解析:(1)设直线的解析表达式为,把A(4,0)、B(3,)代入得:,解得:,所以直线的解析表达式为;
(2)解方程组:,得:,则C(2,﹣3);当y=0时,,解得x=1,则D(1,0),所以△ADC的面积=×(4﹣1)×3=;
(3)因为点D与点C到AD的距离相等,所以D点的纵坐标为3,当y=3时,,解得x=6,所以D点坐标为(6,3).
考点:两条直线相交或平行问题.
23.(1)13,5;(2)等腰直角三角形,理由见解析;(3)当P的坐标为()时,PD+PF的长度最短,最短长度为.
【解析】
【分析】
(1)根据阅读材料中A和B的坐标,利用两点间的距离公式即可得出答案;由于M、N在平行于y轴的直线上,根据M和N的纵坐标利用公式即可求出MN的距离;
(2)由三个顶点的坐标分别求出DE,DF,EF的长,即可判定此三角形的形状;
(3)作F关于x轴的对称点,连接,与x轴交于点P,此时最短,最短距离为,P的坐标即为直线与x轴的交点.
【详解】
解:(1)∵、
∴
故A、B两点间的距离为:13.
∵M、N在平行于y轴的直线上,点M的纵坐标为4,点N的纵坐标为-1
∴
故M、N两点的距离为5.
(2)∵、、
∴
∴DE=DF,
∴△DEF为等腰直角三角形
(3)
作F关于x轴的对称点,连接,与x轴交于点P,此时DP+PF最短
设直线的解析式为y=kx+b
将D(1,6),(4,-2)代入得:
解得
∴直线的解析式为:
令y=0,解得,即P的坐标为()
∵PF=
∴PD+PF=PD+==
故当P的坐标为()时,PD+PF的长度最短,最短长度为.
【点睛】
本题属于一次函数综合题,待定系数法求一次函数解析式以及一次函数与x轴的交点,弄清楚材料中的距离公式是解决本题的关键.
试卷第1页,总3页
试卷第1页,总3页
