人教A版高中数学选修4-41.1.2平面直角坐标系中的伸缩变换教案
文档属性
| 名称 | 人教A版高中数学选修4-41.1.2平面直角坐标系中的伸缩变换教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 53.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-24 15:45:56 | ||
图片预览


文档简介
1.1.2 平面直角坐标系中的伸缩变换
教学目标:
知识与技能:平面直角坐标系中的坐标变换
过程与方法:体会坐标变换的作用
情感、态度与价值观:通过观察、探索、发现的创造性过程,培养创新意识
教学重点:理解平面直角坐标系中的坐标变换、伸缩变换
教学难点:会用坐标变换、伸缩变换解决实际问题
授课类型:新授课
教学措施与方法:启发、诱导发现教学.
教学过程:
一.复习引入
在三角函数图象的学习中,我们研究过下面一些问题:
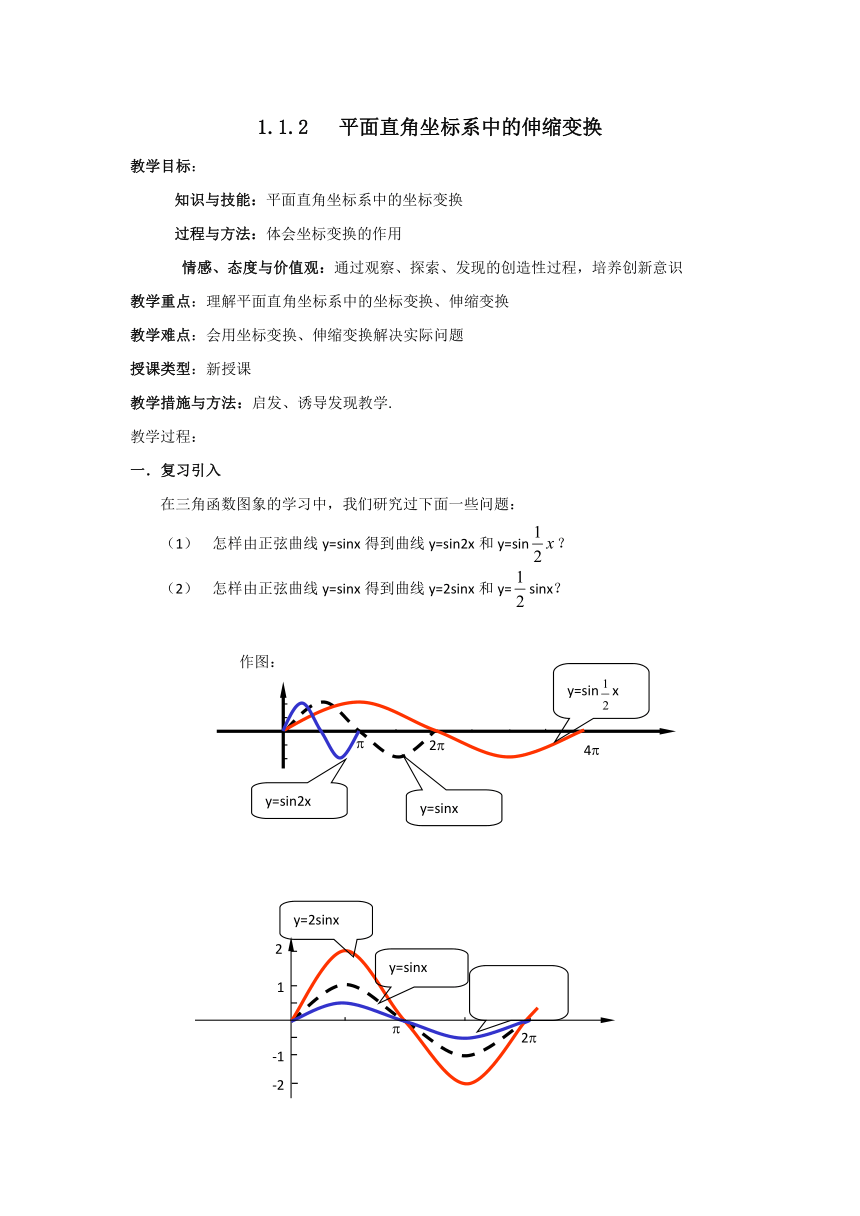
怎样由正弦曲线y=sinx得到曲线y=sin2x和y=sin?
怎样由正弦曲线y=sinx得到曲线y=2sinx和y=sinx?
作图:
二.新课讲解
引导, 观察启发 与y=sinx的图象作比较,结论:
1.函数y=sinωx, x?R (ω>0且ω?1)的图象,可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的倍(纵坐标不变)。
2.y=Asinx,x?R(A>0且A?1)的图象可以看作把正数曲线上的所有点的纵坐标伸长(A>1)或缩短(0设P(x,y)是平面直角坐标系中的任意一点,保持纵坐标y不变,将横坐标x缩为原来的倍,得到P’(x’,y’),那么 ①
我们把①式叫做平面直角坐标系中的一个坐标压缩变换。
设P(x,y)是平面直角坐标系中的任意一点,保持横坐标x不变,将纵坐标y伸长为原来的2倍,得到P’(x’,y’),那么 ②
我们把②式叫做平面直角坐标系中的一个坐标伸长变换。
提出问题:怎样由正弦曲线得到曲线y=2sin2x?(它是由①②两种变换合成的)平面直角坐标系中的任意一点P(x,y),经过上述变换后变为点P’(x’,y’),那么 ③
我们把③式叫做平面直角坐标系中的坐标伸缩变换。
定义:设P(x,y)是平面直角坐标系中的任意一点,在变换 ④的作用下,点P(x,y)对应到点P’(x’,y’),称为平面直角坐标系中的坐标伸缩变换,简称伸缩变换。
三.例题讲解
例1 在平面直角坐标系中,求下列方程所对应的图形经过伸缩变换后的图形。
(1)2x+3y=0; (2)x2+y2=1
在同一平面坐标系中,经过伸缩变换后,曲线C变为曲线,求曲线C的方程并画出图象。
三、知识应用:
1、已知(的图象可以看作把的图象在其所在的坐标系中的横坐标压缩到原来的倍(纵坐标不变)而得到的,则为( )
A. B .2 C.3 D.
2、在同一直角坐标系中,经过伸缩变换后,曲线C变为曲线则曲线C的方程为( )
A. B.C. D.
3、在平面直角坐标系中,求下列方程所对应的图形经过伸缩变换后的图形。
(1)
(2)。
四、知识归纳:设点P(x,y)是平面直角坐标系中的任意一点,在变换
的作用下,点P(x,y)对应到点,称为平面直角坐标系中的坐标伸缩变换
五、作业布置:
1、抛物线经过伸缩变换后得到
2、把圆变成椭圆的伸缩变换为
3、在同一坐标系中将直线变成直线的伸缩变换为
4、把曲线的图象经过伸缩变换得到的图象所对应的方程为
5、在同一平面直角坐标系中,经过伸缩变换后,曲线C变为,则曲线C的方程
六、反思:
教学目标:
知识与技能:平面直角坐标系中的坐标变换
过程与方法:体会坐标变换的作用
情感、态度与价值观:通过观察、探索、发现的创造性过程,培养创新意识
教学重点:理解平面直角坐标系中的坐标变换、伸缩变换
教学难点:会用坐标变换、伸缩变换解决实际问题
授课类型:新授课
教学措施与方法:启发、诱导发现教学.
教学过程:
一.复习引入
在三角函数图象的学习中,我们研究过下面一些问题:
怎样由正弦曲线y=sinx得到曲线y=sin2x和y=sin?
怎样由正弦曲线y=sinx得到曲线y=2sinx和y=sinx?
作图:
二.新课讲解
引导, 观察启发 与y=sinx的图象作比较,结论:
1.函数y=sinωx, x?R (ω>0且ω?1)的图象,可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的倍(纵坐标不变)。
2.y=Asinx,x?R(A>0且A?1)的图象可以看作把正数曲线上的所有点的纵坐标伸长(A>1)或缩短(0
我们把①式叫做平面直角坐标系中的一个坐标压缩变换。
设P(x,y)是平面直角坐标系中的任意一点,保持横坐标x不变,将纵坐标y伸长为原来的2倍,得到P’(x’,y’),那么 ②
我们把②式叫做平面直角坐标系中的一个坐标伸长变换。
提出问题:怎样由正弦曲线得到曲线y=2sin2x?(它是由①②两种变换合成的)平面直角坐标系中的任意一点P(x,y),经过上述变换后变为点P’(x’,y’),那么 ③
我们把③式叫做平面直角坐标系中的坐标伸缩变换。
定义:设P(x,y)是平面直角坐标系中的任意一点,在变换 ④的作用下,点P(x,y)对应到点P’(x’,y’),称为平面直角坐标系中的坐标伸缩变换,简称伸缩变换。
三.例题讲解
例1 在平面直角坐标系中,求下列方程所对应的图形经过伸缩变换后的图形。
(1)2x+3y=0; (2)x2+y2=1
在同一平面坐标系中,经过伸缩变换后,曲线C变为曲线,求曲线C的方程并画出图象。
三、知识应用:
1、已知(的图象可以看作把的图象在其所在的坐标系中的横坐标压缩到原来的倍(纵坐标不变)而得到的,则为( )
A. B .2 C.3 D.
2、在同一直角坐标系中,经过伸缩变换后,曲线C变为曲线则曲线C的方程为( )
A. B.C. D.
3、在平面直角坐标系中,求下列方程所对应的图形经过伸缩变换后的图形。
(1)
(2)。
四、知识归纳:设点P(x,y)是平面直角坐标系中的任意一点,在变换
的作用下,点P(x,y)对应到点,称为平面直角坐标系中的坐标伸缩变换
五、作业布置:
1、抛物线经过伸缩变换后得到
2、把圆变成椭圆的伸缩变换为
3、在同一坐标系中将直线变成直线的伸缩变换为
4、把曲线的图象经过伸缩变换得到的图象所对应的方程为
5、在同一平面直角坐标系中,经过伸缩变换后,曲线C变为,则曲线C的方程
六、反思:
