人教A版高中数学必修一1.3.1函数的单调性教案
文档属性
| 名称 | 人教A版高中数学必修一1.3.1函数的单调性教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 311.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-24 00:00:00 | ||
图片预览


文档简介
1.3.1函数的单调性
一、教学目标:
1.知识与技能:
从形与数两方面理解函数单调性的概念。初步掌握利用图像和定义判断、证明函数单调性的方法。
2.过程与方法:
从已有知识出发,通过学生的观察、归纳、抽象和推理论证培养学生的数学能力。
3.情感态度价值观:
通过知识的探究过程,突出学生的主观能动性,培养学生认真分析、科学论证的数学思维习惯.
二.重点难点?
重点:函数单调性的概念;判断、证明函数的单调性。
难点:函数单调性概念的符号语言的认知;应用定义证明单调性的代数推理论证。
三、教学方法
问题引导,主动探究,启发式教学.
四、教学过程
(1)情景导入
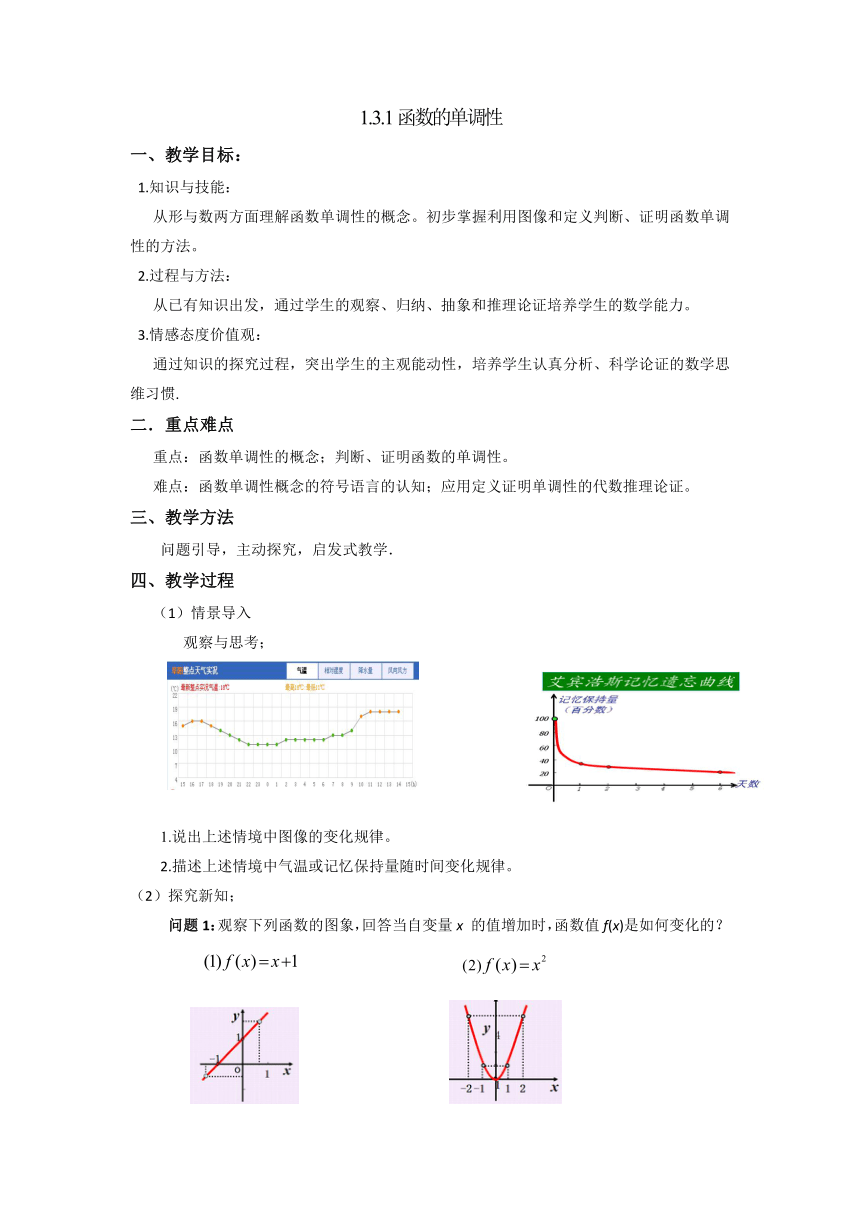
观察与思考;
1.说出上述情境中图像的变化规律。
2.描述上述情境中气温或记忆保持量随时间变化规律。
(2)探究新知;
问题1:观察下列函数的图象,回答当自变量x 的值增加时,函数值f(x)是如何变化的?
问题2:你能根据自己的理解说说什么是递增什么是递减?
问题3:你能借助数学符号,将上述“函数值随着自变量增大逐渐增大”描述出来吗?
当x增大时 f(x)随着增大,即:当x1<x2时,都有f(x1)<f(x2)。
增函数的定义:一般地,设函数f(x)的定义域为I:如果对于定义域I内某个区间上的任意两个自变量的值x1、x2 ,当时,都有,那么就说函数f(x)在区间上是增函数。
概念辨析
问题4:同学们能否类似地得出减函数的定义?(学生讨论、回答)
师生共同得出:定义:一般地,设函数f(x)的定义域为I:如果对于定义域I内某个区间上的任意两个自变量的值x1、x2 ,当时,都有,那么就说函数f(x)在区间上是减函数。
例1 下图是定义在区间上的函数,根据函数图象说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数?
师生活动:学生观察图象,独立完成,教师解答学生在解决问题过程中出现的问题.如:
①单调区间是定义域的子集;
②本题中,如果用并集符号,不符合单调性定义;
③本题中,区端点处有意义,那么区间开闭都可以.
例2.证明函数在上是减函数.
证明:任取, 取值
∴即
∴函数在上是减函数
跟踪训练1. 画出反比例函数的图象。
1)这个函数的定义域I是什么?
2)它在定义域I上的单调性是怎样的?证明你的结论。
总结证明函数单调性的步骤:1.设值:设任意x1、x2属于给定区间,且;
2.作差:差; 3.变形:变形的常用方法有:因式分解、配方、有理化等;
4.判号:确定的正负; 5.下结论:由定义得出函数的单调性。
跟踪训练2.证明 函数的单调性。
五、当堂检测
1.函数y=3x-2x2+1的单调递增区间是(B )
2. 若函数是上的增函数,对于实数,若,则有(A )
3. 函数f(x+1)=x2-2x+1的定义域是,则f(x)的单调递减区间是________.
4. 函数y=的单调减区间为(-∞,0).
5.讨论函数在上的单调性.
解:
设,则∴
∵
当时,,此时函数在上是单调减函数;
当时,,此时函数在上是单调增函数;
六、课堂小结
1.增函数、减函数的定义;
2.图象法判断函数的单调性:增函数的图象从左到右上升,减函数的图象从左到右下降.
3.(定义法)证明函数单调性的步骤:设值、作差、变形、判号、下结论。
七、课后作业
课时练与测
八、教学反思
一、教学目标:
1.知识与技能:
从形与数两方面理解函数单调性的概念。初步掌握利用图像和定义判断、证明函数单调性的方法。
2.过程与方法:
从已有知识出发,通过学生的观察、归纳、抽象和推理论证培养学生的数学能力。
3.情感态度价值观:
通过知识的探究过程,突出学生的主观能动性,培养学生认真分析、科学论证的数学思维习惯.
二.重点难点?
重点:函数单调性的概念;判断、证明函数的单调性。
难点:函数单调性概念的符号语言的认知;应用定义证明单调性的代数推理论证。
三、教学方法
问题引导,主动探究,启发式教学.
四、教学过程
(1)情景导入
观察与思考;
1.说出上述情境中图像的变化规律。
2.描述上述情境中气温或记忆保持量随时间变化规律。
(2)探究新知;
问题1:观察下列函数的图象,回答当自变量x 的值增加时,函数值f(x)是如何变化的?
问题2:你能根据自己的理解说说什么是递增什么是递减?
问题3:你能借助数学符号,将上述“函数值随着自变量增大逐渐增大”描述出来吗?
当x增大时 f(x)随着增大,即:当x1<x2时,都有f(x1)<f(x2)。
增函数的定义:一般地,设函数f(x)的定义域为I:如果对于定义域I内某个区间上的任意两个自变量的值x1、x2 ,当时,都有,那么就说函数f(x)在区间上是增函数。
概念辨析
问题4:同学们能否类似地得出减函数的定义?(学生讨论、回答)
师生共同得出:定义:一般地,设函数f(x)的定义域为I:如果对于定义域I内某个区间上的任意两个自变量的值x1、x2 ,当时,都有,那么就说函数f(x)在区间上是减函数。
例1 下图是定义在区间上的函数,根据函数图象说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数?
师生活动:学生观察图象,独立完成,教师解答学生在解决问题过程中出现的问题.如:
①单调区间是定义域的子集;
②本题中,如果用并集符号,不符合单调性定义;
③本题中,区端点处有意义,那么区间开闭都可以.
例2.证明函数在上是减函数.
证明:任取, 取值
∴即
∴函数在上是减函数
跟踪训练1. 画出反比例函数的图象。
1)这个函数的定义域I是什么?
2)它在定义域I上的单调性是怎样的?证明你的结论。
总结证明函数单调性的步骤:1.设值:设任意x1、x2属于给定区间,且;
2.作差:差; 3.变形:变形的常用方法有:因式分解、配方、有理化等;
4.判号:确定的正负; 5.下结论:由定义得出函数的单调性。
跟踪训练2.证明 函数的单调性。
五、当堂检测
1.函数y=3x-2x2+1的单调递增区间是(B )
2. 若函数是上的增函数,对于实数,若,则有(A )
3. 函数f(x+1)=x2-2x+1的定义域是,则f(x)的单调递减区间是________.
4. 函数y=的单调减区间为(-∞,0).
5.讨论函数在上的单调性.
解:
设,则∴
∵
当时,,此时函数在上是单调减函数;
当时,,此时函数在上是单调增函数;
六、课堂小结
1.增函数、减函数的定义;
2.图象法判断函数的单调性:增函数的图象从左到右上升,减函数的图象从左到右下降.
3.(定义法)证明函数单调性的步骤:设值、作差、变形、判号、下结论。
七、课后作业
课时练与测
八、教学反思
