高中数学必修一 1.2.1《函数的概念》教案
文档属性
| 名称 | 高中数学必修一 1.2.1《函数的概念》教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 49.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-24 00:00:00 | ||
图片预览

文档简介
《函数的概念》教案
教学目标
1、理解函数的概念及其符号表示,能够辨别函数的例证和反例.
2、会求简单函数的定义域与值域.
3、掌握构成函数的三要素,学会判别两个函数是否相等,理解函数的整体性.
4、通过情景,进一步体会函数是描述变量之间的依赖关系的重要数学模型,在此基础上学习用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用.
5、通过函数概念学习的过程,培养学生从“特殊到一般”的分析问题能力以及抽象概括能力.
教学重难点
重点:函数的概念,构成函数的三要素.
难点:函数符号y=f(x)的理解.
教学过程
一、情景导入
情景一:
一枚炮弹发射后,经过26s落到地面击中目标.炮弹的射高为845m,且炮弹距地面的高度h(单位:m)随时间t(单位:s)变化的规律是:
;
提问:你能得出炮弹飞行5秒、10秒、20秒时距地面多高吗?其中,时间t的变化范围是什么?炮弹距离地面高度h的变化范围是什么?
情景二:
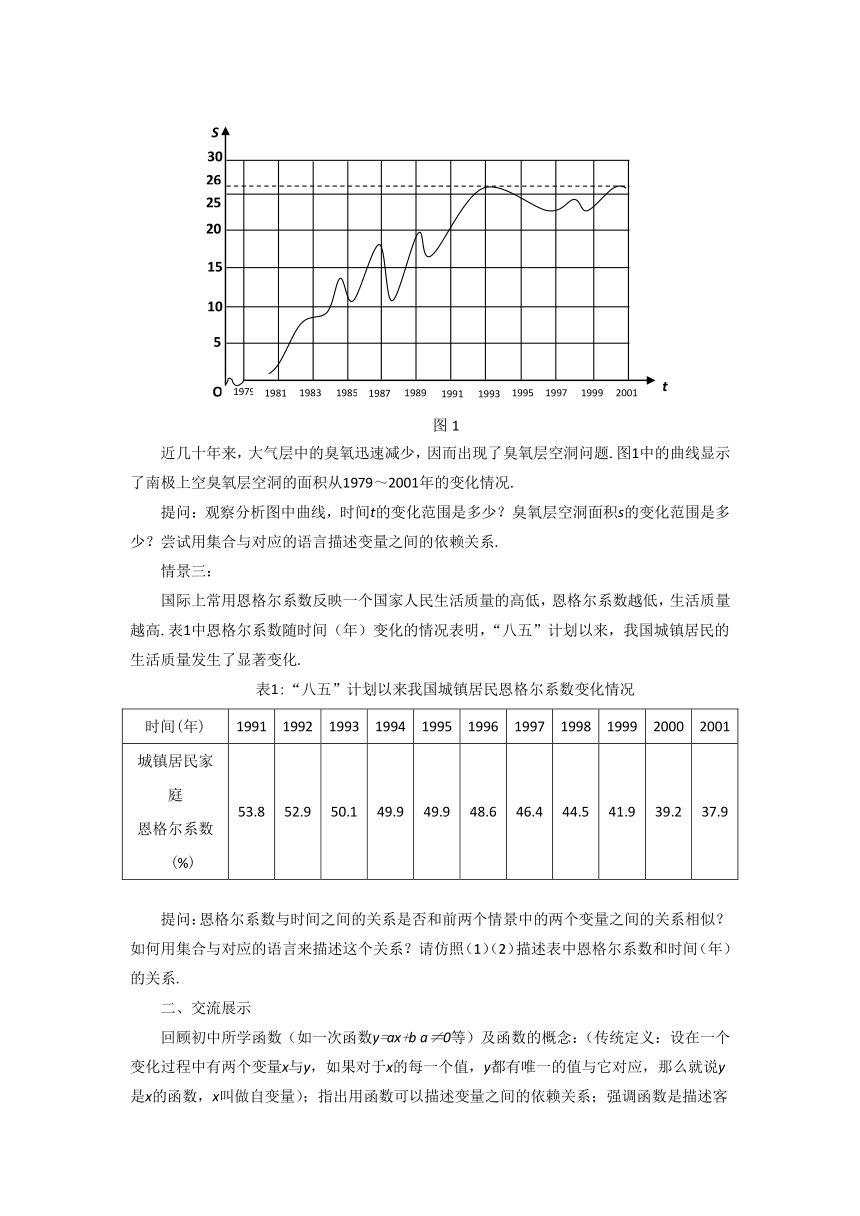
近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题.图1中的曲线显示了南极上空臭氧层空洞的面积从1979~2001年的变化情况.
提问:观察分析图中曲线,时间t的变化范围是多少?臭氧层空洞面积s的变化范围是多少?尝试用集合与对应的语言描述变量之间的依赖关系.
情景三:
国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高.表1中恩格尔系数随时间(年)变化的情况表明,“八五”计划以来,我国城镇居民的生活质量发生了显著变化.
表1:“八五”计划以来我国城镇居民恩格尔系数变化情况
时间(年)
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
城镇居民家庭
恩格尔系数(%)
53.8
52.9
50.1
49.9
49.9
48.6
46.4
44.5
41.9
39.2
37.9
提问:恩格尔系数与时间之间的关系是否和前两个情景中的两个变量之间的关系相似?如何用集合与对应的语言来描述这个关系?请仿照(1)(2)描述表中恩格尔系数和时间(年)的关系.
二、交流展示
回顾初中所学函数(如一次函数y=ax+b a≠0等)及函数的概念:(传统定义:设在一个变化过程中有两个变量x与y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说y是x的函数,x叫做自变量);指出用函数可以描述变量之间的依赖关系;强调函数是描述客观世界变化规律的重要数学模型.
三、合作探究
(1)(小组讨论)思考:分析、归纳以上三个情景,变量之间的关系有什么不同点和共同点?
归纳以上三个情景,可看出其不同点是:情景一是用解析式刻画变量之间的对应关系,情景二是用图像刻画变量之间的对应关系,情景三是用表格刻画变量之间的对应关系.
其共同点是:①都有两个非空数集A和B;②两个数集之间都有一种确定的对应关系;③对于数集A中的每一个x,按照某种对应关系f,在数集B中都有唯一确定的y值和它对应.记作
(2)函数的概念(让学生用集合与对应的语言刻画函数,抽象概括出函数的概念)
一般地,设A,B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称为从集合A到集合B的一个函数,记作.
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合叫做函数的值域.
显然,值域是集合B的子集.().
解剖分析:
①函数是两个数集之间建立的对应
②“任意”、“唯一”
③认真理解的含义:
是一个整体,并不表示f与x的乘积,它是一种符号,它可以是解析式,如情景一;也可以是图像,如情景二;也可以是表格,如情景三;如同一个加工厂,把把输入的数x,按照某种加工过程如解析式,图像,表格,加工称另外一个数值y.
(3)区间的概念.
学生要明确以下几点:
①区间的左端点必小于右端点
②以“”或“”为区间一端时,这一端必须是小括号
学生独自完成下列表格(可以用区间表示)
函数
一次函数
二次函数
反比例函数
对应关系
定义域
值域
例1、已知函数,
(1)求函数的定义域;
(2)求的值;
(3)当时,求的值.
分析:函数的定义域通常由问题的实际背景确定,如前所述的三个实例。如果只给出解析式,而没有指明它的定义域,那么函数的定义域就是指能使这个式子有意义的的实数的集合。
解:(1)使根式有意义的实数的集合是,使分式有意义的实数的集合是,所以,这个函数的定义域是.
(2)
(3)因为,所以有意义
;
.
例2、下列函数中哪个与函数相等?
(1);(2)
(3);(4)
解:(1)对应关系相同,但是定义域不相同,函数不相等;
(2)对应关系相同,定义域相同,函数相等;
(3)对应关系相同,但是定义域不相同,函数不相等;
(4)对应关系相同,但是定义域不相同,函数不相等.
四、课堂小结
函数的概念;函数的三要素;如何判断两个函数是否相等.
五、巩固练习
1、判断下列对应是否为函数
(1)(xR)(2)
(3)
2、求下列函数的定义域
①②
③+④
⑤
六、布置作业
课后练习2、3
教学目标
1、理解函数的概念及其符号表示,能够辨别函数的例证和反例.
2、会求简单函数的定义域与值域.
3、掌握构成函数的三要素,学会判别两个函数是否相等,理解函数的整体性.
4、通过情景,进一步体会函数是描述变量之间的依赖关系的重要数学模型,在此基础上学习用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用.
5、通过函数概念学习的过程,培养学生从“特殊到一般”的分析问题能力以及抽象概括能力.
教学重难点
重点:函数的概念,构成函数的三要素.
难点:函数符号y=f(x)的理解.
教学过程
一、情景导入
情景一:
一枚炮弹发射后,经过26s落到地面击中目标.炮弹的射高为845m,且炮弹距地面的高度h(单位:m)随时间t(单位:s)变化的规律是:
;
提问:你能得出炮弹飞行5秒、10秒、20秒时距地面多高吗?其中,时间t的变化范围是什么?炮弹距离地面高度h的变化范围是什么?
情景二:
近几十年来,大气层中的臭氧迅速减少,因而出现了臭氧层空洞问题.图1中的曲线显示了南极上空臭氧层空洞的面积从1979~2001年的变化情况.
提问:观察分析图中曲线,时间t的变化范围是多少?臭氧层空洞面积s的变化范围是多少?尝试用集合与对应的语言描述变量之间的依赖关系.
情景三:
国际上常用恩格尔系数反映一个国家人民生活质量的高低,恩格尔系数越低,生活质量越高.表1中恩格尔系数随时间(年)变化的情况表明,“八五”计划以来,我国城镇居民的生活质量发生了显著变化.
表1:“八五”计划以来我国城镇居民恩格尔系数变化情况
时间(年)
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
城镇居民家庭
恩格尔系数(%)
53.8
52.9
50.1
49.9
49.9
48.6
46.4
44.5
41.9
39.2
37.9
提问:恩格尔系数与时间之间的关系是否和前两个情景中的两个变量之间的关系相似?如何用集合与对应的语言来描述这个关系?请仿照(1)(2)描述表中恩格尔系数和时间(年)的关系.
二、交流展示
回顾初中所学函数(如一次函数y=ax+b a≠0等)及函数的概念:(传统定义:设在一个变化过程中有两个变量x与y,如果对于x的每一个值,y都有唯一的值与它对应,那么就说y是x的函数,x叫做自变量);指出用函数可以描述变量之间的依赖关系;强调函数是描述客观世界变化规律的重要数学模型.
三、合作探究
(1)(小组讨论)思考:分析、归纳以上三个情景,变量之间的关系有什么不同点和共同点?
归纳以上三个情景,可看出其不同点是:情景一是用解析式刻画变量之间的对应关系,情景二是用图像刻画变量之间的对应关系,情景三是用表格刻画变量之间的对应关系.
其共同点是:①都有两个非空数集A和B;②两个数集之间都有一种确定的对应关系;③对于数集A中的每一个x,按照某种对应关系f,在数集B中都有唯一确定的y值和它对应.记作
(2)函数的概念(让学生用集合与对应的语言刻画函数,抽象概括出函数的概念)
一般地,设A,B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称为从集合A到集合B的一个函数,记作.
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合叫做函数的值域.
显然,值域是集合B的子集.().
解剖分析:
①函数是两个数集之间建立的对应
②“任意”、“唯一”
③认真理解的含义:
是一个整体,并不表示f与x的乘积,它是一种符号,它可以是解析式,如情景一;也可以是图像,如情景二;也可以是表格,如情景三;如同一个加工厂,把把输入的数x,按照某种加工过程如解析式,图像,表格,加工称另外一个数值y.
(3)区间的概念.
学生要明确以下几点:
①区间的左端点必小于右端点
②以“”或“”为区间一端时,这一端必须是小括号
学生独自完成下列表格(可以用区间表示)
函数
一次函数
二次函数
反比例函数
对应关系
定义域
值域
例1、已知函数,
(1)求函数的定义域;
(2)求的值;
(3)当时,求的值.
分析:函数的定义域通常由问题的实际背景确定,如前所述的三个实例。如果只给出解析式,而没有指明它的定义域,那么函数的定义域就是指能使这个式子有意义的的实数的集合。
解:(1)使根式有意义的实数的集合是,使分式有意义的实数的集合是,所以,这个函数的定义域是.
(2)
(3)因为,所以有意义
;
.
例2、下列函数中哪个与函数相等?
(1);(2)
(3);(4)
解:(1)对应关系相同,但是定义域不相同,函数不相等;
(2)对应关系相同,定义域相同,函数相等;
(3)对应关系相同,但是定义域不相同,函数不相等;
(4)对应关系相同,但是定义域不相同,函数不相等.
四、课堂小结
函数的概念;函数的三要素;如何判断两个函数是否相等.
五、巩固练习
1、判断下列对应是否为函数
(1)(xR)(2)
(3)
2、求下列函数的定义域
①②
③+④
⑤
六、布置作业
课后练习2、3
