高中数学新人教B版选修1-1课件:2.1.2椭圆的几何性质(18张)
文档属性
| 名称 | 高中数学新人教B版选修1-1课件:2.1.2椭圆的几何性质(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 524.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-24 00:00:00 | ||
图片预览






文档简介
课件18张PPT。2.1.2 椭圆的几何性质 1.掌握椭圆的几何性质.
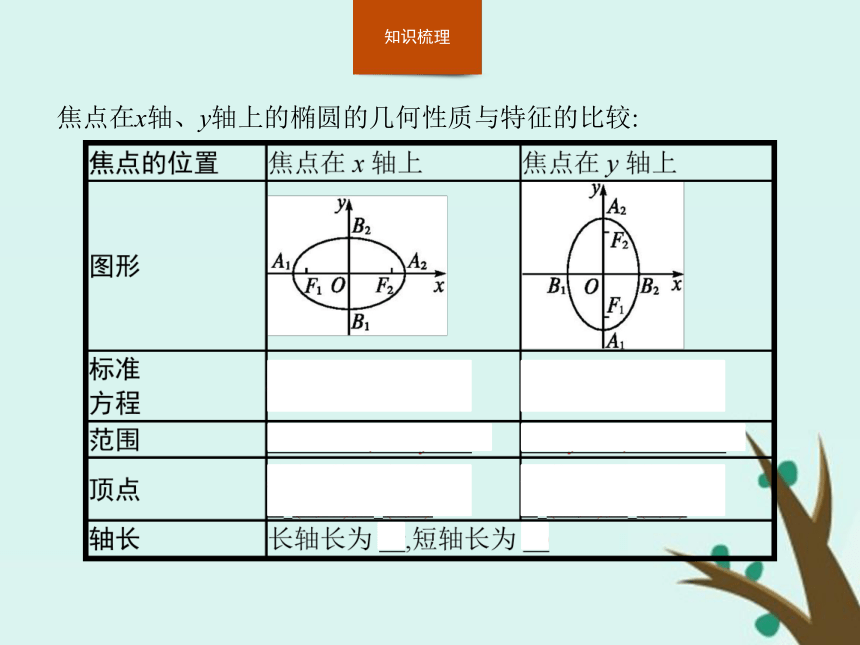
2.掌握椭圆中长半轴长,短半轴长,半焦距和离心率的几何意义以及它们之间的关系.焦点在x轴、y轴上的椭圆的几何性质与特征的比较: 名师点拨(1)判断曲线关于原点,x轴,y轴对称的方法.
若把方程中的x换成-x,y换成-y,方程不变,则曲线关于原点对称.
若把方程中的y换成-y,方程不变,则曲线关于x轴对称.
若把方程中的x换成-x,方程不变,则曲线关于y轴对称.
(2)椭圆的顶点是它与对称轴的交点.题型一题型二题型三利用椭圆的方程研究其几何性质
【例1】 求椭圆25x2+16y2=400的长轴长、短轴长、离心率、焦点坐标和顶点坐标.
分析:先把椭圆方程写成标准形式,求出基本元素长半轴长a、短半轴长b和半焦距c,再求解.题型一题型二题型三反思已知椭圆的方程讨论其性质时,应将方程化成标准形式,找准长半轴长a与短半轴长b,求出半焦距c,才能正确地解决与椭圆的性质有关的问题.题型一题型二题型三利用椭圆的几何性质求它的方程
【例2】 已知椭圆的长轴长是短轴长的2倍,且过点(2,-6),求椭圆的标准方程.
分析:因为不知道椭圆的焦点在哪个坐标轴上,所以需要分两种情况来讨论.题型一题型二题型三题型一题型二题型三 反思在求椭圆的标准方程时,关键要分清焦点在哪个坐标轴上;当焦点不确定在哪个坐标轴上时,要分焦点在x轴上、y轴上两种情况讨论.题型一题型二题型三求椭圆方程中的参数题型一题型二题型三题型一题型二题型三 反思在求椭圆标准方程中的参数时,先要分清焦点在哪个坐标轴上,再根据椭圆的几何性质求解.注意本题所给方程中的a与椭圆标准方程中的a不同.答案:D 解析:由题意无法确定焦点在x轴上还是在y轴上,则标准方程有两个.由长轴长2a=12,得a=6.答案:C
2.掌握椭圆中长半轴长,短半轴长,半焦距和离心率的几何意义以及它们之间的关系.焦点在x轴、y轴上的椭圆的几何性质与特征的比较: 名师点拨(1)判断曲线关于原点,x轴,y轴对称的方法.
若把方程中的x换成-x,y换成-y,方程不变,则曲线关于原点对称.
若把方程中的y换成-y,方程不变,则曲线关于x轴对称.
若把方程中的x换成-x,方程不变,则曲线关于y轴对称.
(2)椭圆的顶点是它与对称轴的交点.题型一题型二题型三利用椭圆的方程研究其几何性质
【例1】 求椭圆25x2+16y2=400的长轴长、短轴长、离心率、焦点坐标和顶点坐标.
分析:先把椭圆方程写成标准形式,求出基本元素长半轴长a、短半轴长b和半焦距c,再求解.题型一题型二题型三反思已知椭圆的方程讨论其性质时,应将方程化成标准形式,找准长半轴长a与短半轴长b,求出半焦距c,才能正确地解决与椭圆的性质有关的问题.题型一题型二题型三利用椭圆的几何性质求它的方程
【例2】 已知椭圆的长轴长是短轴长的2倍,且过点(2,-6),求椭圆的标准方程.
分析:因为不知道椭圆的焦点在哪个坐标轴上,所以需要分两种情况来讨论.题型一题型二题型三题型一题型二题型三 反思在求椭圆的标准方程时,关键要分清焦点在哪个坐标轴上;当焦点不确定在哪个坐标轴上时,要分焦点在x轴上、y轴上两种情况讨论.题型一题型二题型三求椭圆方程中的参数题型一题型二题型三题型一题型二题型三 反思在求椭圆标准方程中的参数时,先要分清焦点在哪个坐标轴上,再根据椭圆的几何性质求解.注意本题所给方程中的a与椭圆标准方程中的a不同.答案:D 解析:由题意无法确定焦点在x轴上还是在y轴上,则标准方程有两个.由长轴长2a=12,得a=6.答案:C
