高中数学新人教B版选修1-1课件:2.3.2抛物线的几何性质(19张)
文档属性
| 名称 | 高中数学新人教B版选修1-1课件:2.3.2抛物线的几何性质(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 415.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-24 00:00:00 | ||
图片预览






文档简介
课件19张PPT。2.3.2 抛物线的几何性质1.理解抛物线的简单的几何性质.
2.了解抛物线的简单应用.一、抛物线y2=2px(p>0)的几何性质
1.范围
因为p>0,由方程y2=2px(p>0)可知,这条抛物线上任意一点M的坐标(x,y)满足不等式x≥0,所以这条抛物线在y轴的右侧;当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸,它开口向右.
2.对称性
以-y代y,方程y2=2px(p>0)不变,因此这条抛物线是以x轴为对称轴的轴对称图形.抛物线的对称轴叫做抛物线的轴.
3.顶点
抛物线和它的轴的交点叫做抛物线的顶点,在方程y2=2px(p>0)中,当y=0时,x=0,因此这条抛物线的顶点就是坐标原点.4.离心率
抛物线上的点到焦点和准线的距离的比,叫做抛物线的离心率,用e表示.按照抛物线的定义,e=1.
【做一做1】 抛物线y2=4x的顶点坐标是 ,对称轴是 .?
答案:(0,0) x轴(直线y=0)名师点拨抛物线的性质和椭圆、双曲线的区别:
抛物线的离心率等于1,它只有一个焦点、一个顶点、一条对称轴和一条准线.它没有中心,通常称抛物线为无心圆锥曲线,而称椭圆和双曲线为有心圆锥曲线.二、抛物线四种形式的标准方程
在直角坐标平面上,顶点在原点、轴与坐标轴重合的抛物线有四种位置情况,因此抛物线的方程相应地有四种形式,它们都叫做抛物线的标准方程.
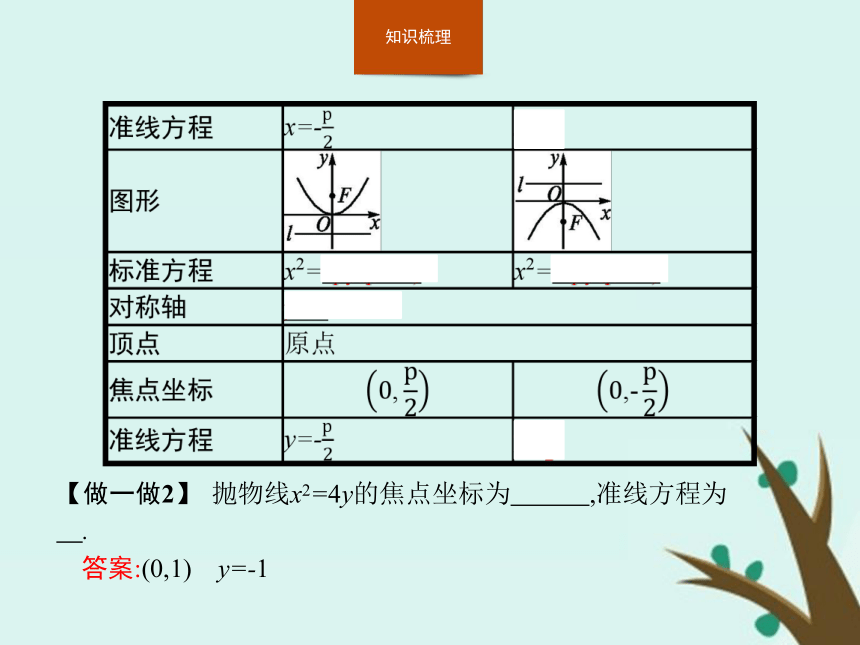
设抛物线的焦参数为p(p>0),抛物线的标准方程的四种形式列表如下:【做一做2】 抛物线x2=4y的焦点坐标为 ,准线方程为 .?
答案:(0,1) y=-1名师点拨(1)对以上四种位置不同的抛物线和它们的标准方程进行对比、分析,其共同点:①顶点都为原点;②对称轴为坐标轴;③准线与对称轴垂直,垂足与焦点分别关于原点对称,它们与原点的距离都等于一次项系数的绝对值的 ;④焦点到准线的距离均为p.其不同点:①对称轴为x轴时,方程的右端为±2px,左端为y2;对称轴为y轴时,方程的右端为±2py,左端为x2;②开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)的正半轴上,方程的右端取正号,开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)的负半轴上,方程的右端取负号.
(2)只有焦点在坐标轴上,顶点是原点的抛物线的方程才是标准方程. 1.焦参数p与抛物线的开口之间有什么关系?
剖析:p是抛物线焦点到准线的距离,由方程y2=2px知,对于同一个x的值,p值越大,|y|也越大,不妨说抛物线开口也越大,这样可以较好地理解不同的p值与抛物线开口大小的关系.
2.如何确定抛物线的对称轴和开口方向?
剖析:已知抛物线的标准方程,求它的焦点坐标和准线方程时,首先要判断抛物线的对称轴和开口方向.一次项的变量若为x(或y),则x轴(或y轴)是抛物线的对称轴,一次项系数的符号决定开口方向.
例如,抛物线的方程为x2=-4y,则y轴为其对称轴,开口方向和y轴的正方向相反.归纳总结对称轴要看一次项,符号确定开口方向,如果y是一次项,y的系数为负时开口向下,y的系数为正时开口向上.如果x是一次项,x的系数为负时开口向左,x的系数为正时开口向右.题型一题型二题型三题型四根据方程研究性质
【例1】 已知抛物线的标准方程如下,分别求出它们的焦点坐标和准线方程.
(1)x2=-8y; (2)2y2+7x=0.
分析:先把所给方程化为标准方程,求出p,再根据开口方向,写出焦点坐标和准线方程.
解:(1)由抛物线的标准方程知抛物线的焦点在y轴的负半轴上,开口向下.
∵p=4,∴焦点坐标为(0,-2),准线方程为y=2.题型一题型二题型三题型四求抛物线的标准方程
【例2】 求分别符合下列条件的抛物线的标准方程.
(1)过点(-3,2);(2)焦点在直线x-2y-4=0上.
分析:根据已知条件求出抛物线标准方程中的p即可,注意标准方程的形式.题型一题型二题型三题型四题型一题型二题型三题型四 反思求抛物线方程常用待定系数法,当抛物线类型不确定时,要注意讨论题型一题型二题型三题型四抛物线的简单应用
【例3】 探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯口圆的直径为60 cm,灯深为40 cm,求抛物线的标准方程和焦点坐标.
分析:建立适当的坐标系确定抛物线上一点的坐标,从而确定焦参数p,求得其方程.题型一题型二题型三题型四 反思解决本题的关键是建立适当的坐标系,求出抛物线的标准方程,进而求出焦点坐标.题型一题型二题型三题型四易错题型
【例4】 设抛物线y2=mx(m≠0)的准线与直线x=1的距离为3,求抛物线方程.2过点(-1,2)的抛物线的标准方程为 .?3焦点在直线x+y=1上的抛物线的标准方程为 .4设抛物线x2=my(m≠0)的焦点到直线y=1的距离为2,则m=_____.5正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,求这个正三角形的边长.
2.了解抛物线的简单应用.一、抛物线y2=2px(p>0)的几何性质
1.范围
因为p>0,由方程y2=2px(p>0)可知,这条抛物线上任意一点M的坐标(x,y)满足不等式x≥0,所以这条抛物线在y轴的右侧;当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸,它开口向右.
2.对称性
以-y代y,方程y2=2px(p>0)不变,因此这条抛物线是以x轴为对称轴的轴对称图形.抛物线的对称轴叫做抛物线的轴.
3.顶点
抛物线和它的轴的交点叫做抛物线的顶点,在方程y2=2px(p>0)中,当y=0时,x=0,因此这条抛物线的顶点就是坐标原点.4.离心率
抛物线上的点到焦点和准线的距离的比,叫做抛物线的离心率,用e表示.按照抛物线的定义,e=1.
【做一做1】 抛物线y2=4x的顶点坐标是 ,对称轴是 .?
答案:(0,0) x轴(直线y=0)名师点拨抛物线的性质和椭圆、双曲线的区别:
抛物线的离心率等于1,它只有一个焦点、一个顶点、一条对称轴和一条准线.它没有中心,通常称抛物线为无心圆锥曲线,而称椭圆和双曲线为有心圆锥曲线.二、抛物线四种形式的标准方程
在直角坐标平面上,顶点在原点、轴与坐标轴重合的抛物线有四种位置情况,因此抛物线的方程相应地有四种形式,它们都叫做抛物线的标准方程.
设抛物线的焦参数为p(p>0),抛物线的标准方程的四种形式列表如下:【做一做2】 抛物线x2=4y的焦点坐标为 ,准线方程为 .?
答案:(0,1) y=-1名师点拨(1)对以上四种位置不同的抛物线和它们的标准方程进行对比、分析,其共同点:①顶点都为原点;②对称轴为坐标轴;③准线与对称轴垂直,垂足与焦点分别关于原点对称,它们与原点的距离都等于一次项系数的绝对值的 ;④焦点到准线的距离均为p.其不同点:①对称轴为x轴时,方程的右端为±2px,左端为y2;对称轴为y轴时,方程的右端为±2py,左端为x2;②开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)的正半轴上,方程的右端取正号,开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)的负半轴上,方程的右端取负号.
(2)只有焦点在坐标轴上,顶点是原点的抛物线的方程才是标准方程. 1.焦参数p与抛物线的开口之间有什么关系?
剖析:p是抛物线焦点到准线的距离,由方程y2=2px知,对于同一个x的值,p值越大,|y|也越大,不妨说抛物线开口也越大,这样可以较好地理解不同的p值与抛物线开口大小的关系.
2.如何确定抛物线的对称轴和开口方向?
剖析:已知抛物线的标准方程,求它的焦点坐标和准线方程时,首先要判断抛物线的对称轴和开口方向.一次项的变量若为x(或y),则x轴(或y轴)是抛物线的对称轴,一次项系数的符号决定开口方向.
例如,抛物线的方程为x2=-4y,则y轴为其对称轴,开口方向和y轴的正方向相反.归纳总结对称轴要看一次项,符号确定开口方向,如果y是一次项,y的系数为负时开口向下,y的系数为正时开口向上.如果x是一次项,x的系数为负时开口向左,x的系数为正时开口向右.题型一题型二题型三题型四根据方程研究性质
【例1】 已知抛物线的标准方程如下,分别求出它们的焦点坐标和准线方程.
(1)x2=-8y; (2)2y2+7x=0.
分析:先把所给方程化为标准方程,求出p,再根据开口方向,写出焦点坐标和准线方程.
解:(1)由抛物线的标准方程知抛物线的焦点在y轴的负半轴上,开口向下.
∵p=4,∴焦点坐标为(0,-2),准线方程为y=2.题型一题型二题型三题型四求抛物线的标准方程
【例2】 求分别符合下列条件的抛物线的标准方程.
(1)过点(-3,2);(2)焦点在直线x-2y-4=0上.
分析:根据已知条件求出抛物线标准方程中的p即可,注意标准方程的形式.题型一题型二题型三题型四题型一题型二题型三题型四 反思求抛物线方程常用待定系数法,当抛物线类型不确定时,要注意讨论题型一题型二题型三题型四抛物线的简单应用
【例3】 探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯口圆的直径为60 cm,灯深为40 cm,求抛物线的标准方程和焦点坐标.
分析:建立适当的坐标系确定抛物线上一点的坐标,从而确定焦参数p,求得其方程.题型一题型二题型三题型四 反思解决本题的关键是建立适当的坐标系,求出抛物线的标准方程,进而求出焦点坐标.题型一题型二题型三题型四易错题型
【例4】 设抛物线y2=mx(m≠0)的准线与直线x=1的距离为3,求抛物线方程.2过点(-1,2)的抛物线的标准方程为 .?3焦点在直线x+y=1上的抛物线的标准方程为 .4设抛物线x2=my(m≠0)的焦点到直线y=1的距离为2,则m=_____.5正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y2=2px(p>0)上,求这个正三角形的边长.
