高中数学新人教A版选修4-1课件:1.1平行线等分线段定理(21张)
文档属性
| 名称 | 高中数学新人教A版选修4-1课件:1.1平行线等分线段定理(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 735.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 09:39:51 | ||
图片预览




文档简介
课件21张PPT。第一讲 相似三角形的判定及有关性质一 平行线等分线段定理1.理解并掌握平行线等分线段定理及其推论,认识它的图形语言及变式图形.
2.能运用平行线等分线段定理任意等分已知线段,能运用推论进行简单的证明或计算.
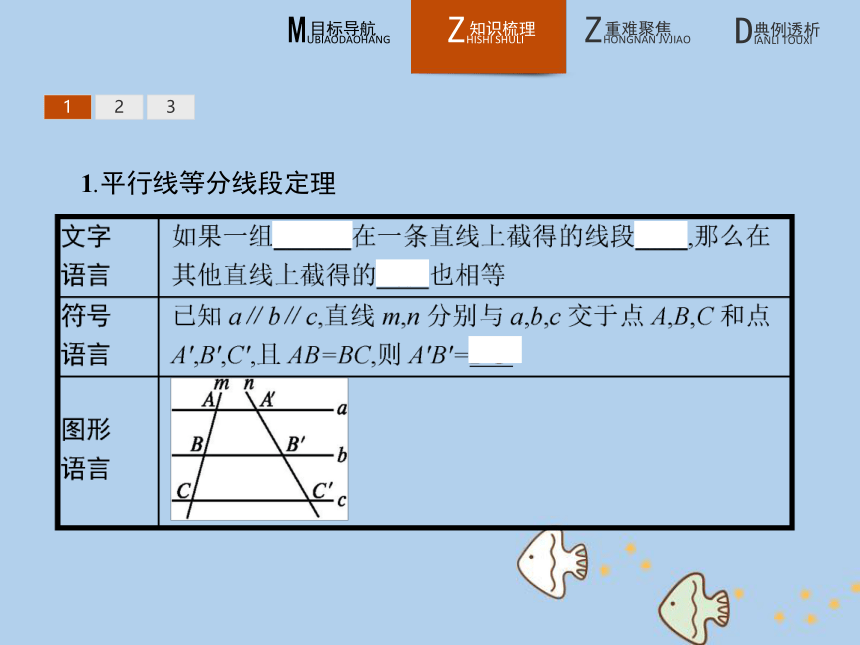
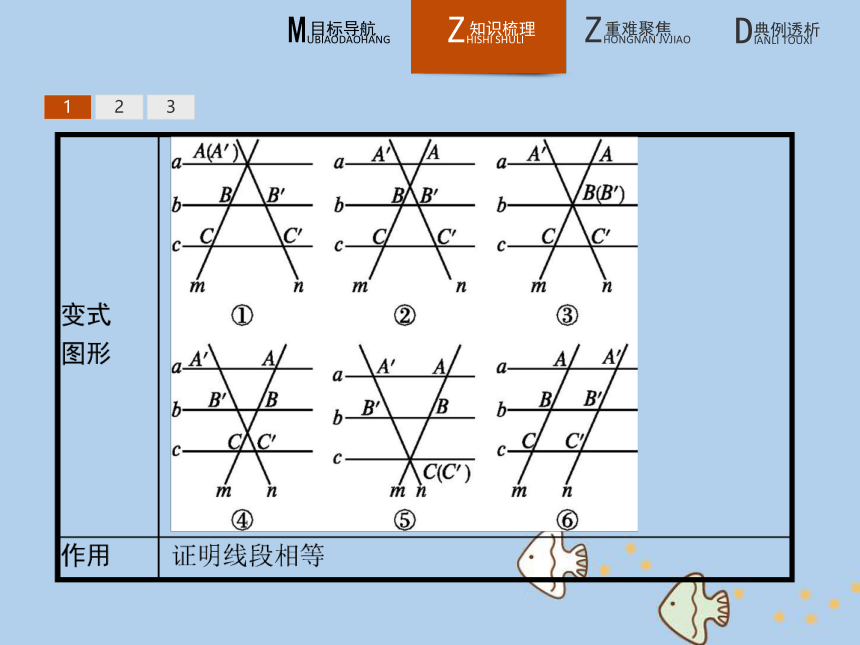
3.会用三角形中位线定理解决问题.1231.平行线等分线段定理 123123名师点拨1.平行线等分线段定理的条件是a,b,c互相平行,构成一组平行线,m与n可以平行,也可以相交,但它们必须与已知的平行线a,b,c相交,即被平行线a,b,c所截.
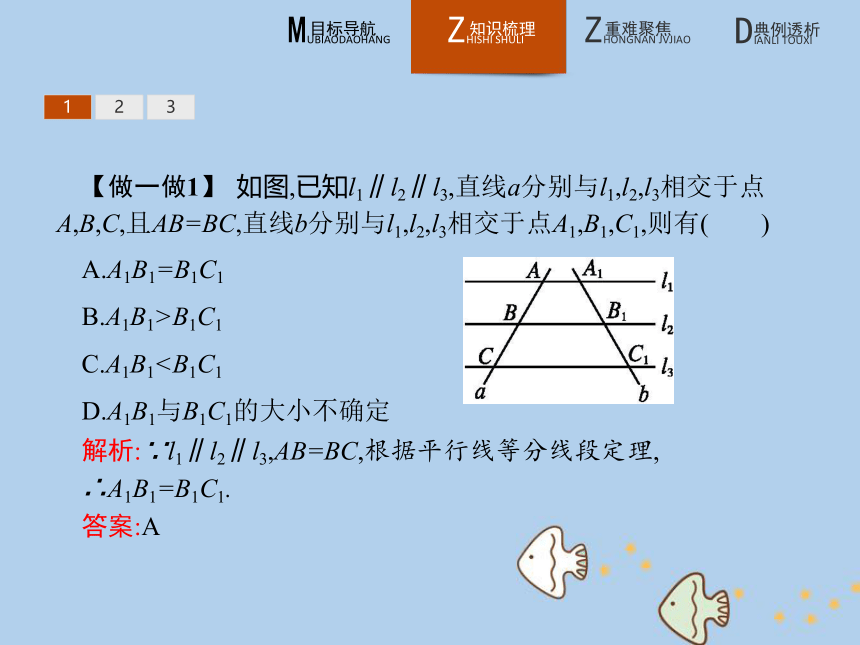
2.平行线的条数可以多于3条,该定理还可以推广.123【做一做1】 如图,已知l1∥l2∥l3,直线a分别与l1,l2,l3相交于点A,B,C,且AB=BC,直线b分别与l1,l2,l3相交于点A1,B1,C1,则有( )
A.A1B1=B1C1
B.A1B1>B1C1
C.A1B1D.A1B1与B1C1的大小不确定
解析:∵l1∥l2∥l3,AB=BC,根据平行线等分线段定理,
∴A1B1=B1C1.
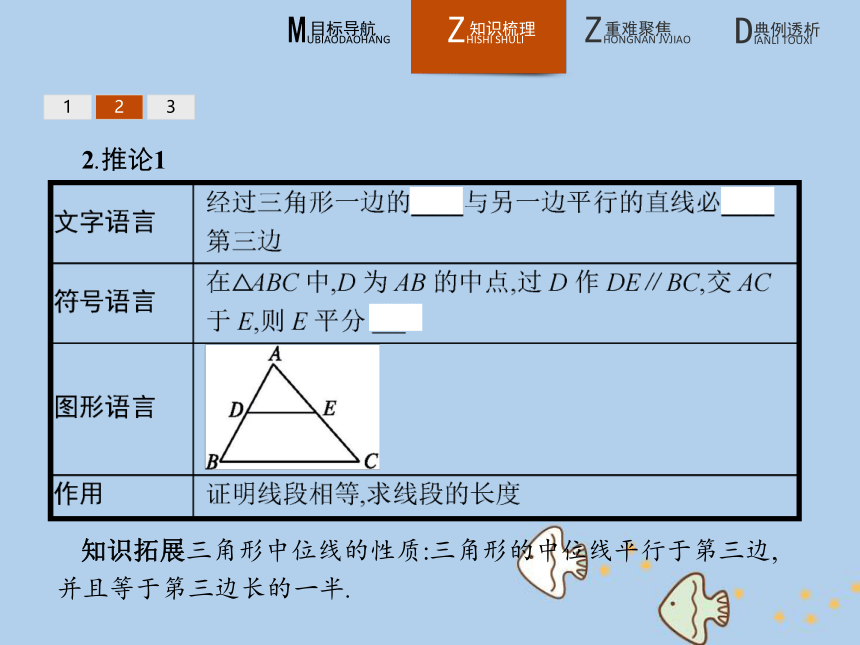
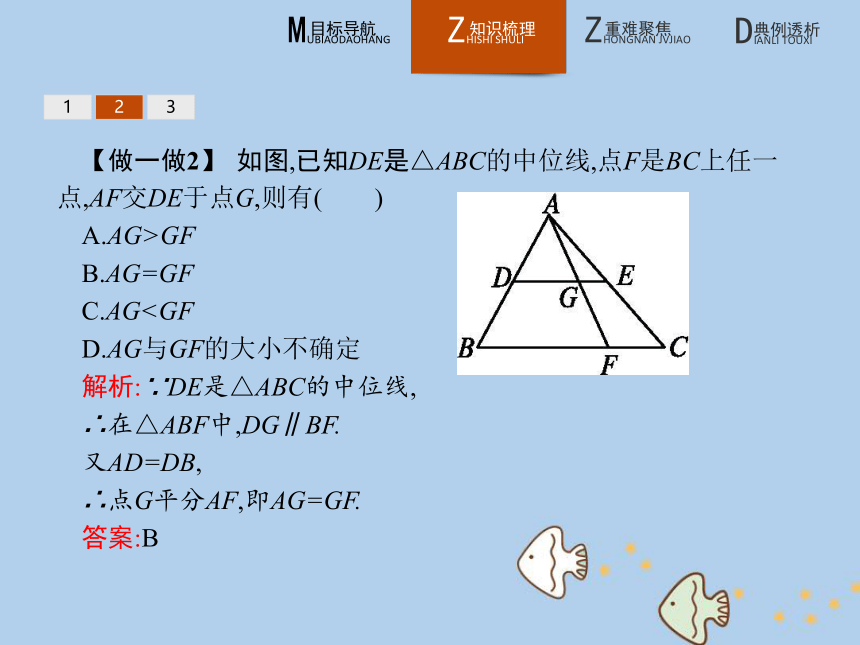
答案:A1232.推论1 知识拓展三角形中位线的性质:三角形的中位线平行于第三边,并且等于第三边长的一半.123【做一做2】 如图,已知DE是△ABC的中位线,点F是BC上任一点,AF交DE于点G,则有( )
A.AG>GF
B.AG=GF
C.AGD.AG与GF的大小不确定
解析:∵DE是△ABC的中位线,
∴在△ABF中,DG∥BF.
又AD=DB,
∴点G平分AF,即AG=GF.
答案:B1233.推论2
知识拓展梯形中位线的性质:梯形的中位线平行于两底边,并且等于两底边长和的一半.123【做一做3】 如图,已知在梯形ABCD中,AD∥BC,AD+BC=10 cm,E为AB的中点,点F在DC上,且EF∥AD,则EF的长为( )
A.5 cm
B.10 cm
C.20 cm
D.不确定
解析:由推论2知,EF是梯形ABCD的中位线,
答案:A平行线等分线段定理的两个推论的证明
剖析:(1)推论1,如图①,在△ABC中,B'为AB的中点,过点B'作B'C'∥BC交AC于点C',求证:点C'是AC的中点.证明:如图②,过点A作直线a∥BC,
∵BC∥B'C',∴a∥BC∥B'C'.
∵AB'=BB',∴AC'=CC',
即点C'是AC的中点.
(2)推论2,如图③,已知在梯形ACC'A'中,AA'∥CC',B是AC的中点,过点B作BB'∥CC'交A'C'于点B',求证:点B'是A'C'的中点.
证明:如图④,∵AA'∥CC',BB'∥CC',
∴AA'∥BB'∥CC'.
∵AB=BC,
∴A'B'=B'C',即点B'是A'C'的中点.题型一题型二题型三【例1】 如图,已知线段AB,求作线段AB的五等分点,并予以证明.
分析:利用平行线等分线段定理来作图.
作法:如图,(1)作射线AC;
(2)在射线AC上以任意取定的长度顺次截取AD1=D1D2=D2D3=D3D4=D4D5;
(3)连接D5B;
(4)分别过D1,D2,D3,D4作D5B的平行线D1A1,D2A2,D3A3,D4A4,分别交AB于点A1,A2,A3,A4,则点A1,A2,A3,A4将线段AB五等分.题型一题型二题型三证明:过点A作MN∥D5B.
则MN∥D4A4∥D3A3∥D2A2∥D1A1∥D5B.
∵AD1=D1D2=D2D3=D3D4=D4D5.
∴AA1=A1A2=A2A3=A3A4=A4B.
∴点A1,A2,A3,A4就是所求的线段AB的五等分点.
反思将已知线段AB分成n等份的解题步骤如下:
(1)作射线AC(与AB不共线);
(2)在射线AC上以任意取定的长度顺次截取AD1=D1D2=D2D3=…=Dn-1Dn;
(3)连接DnB;
(4)分别过点D1,D2,D3,…,Dn-2,Dn-1作DnB的平行线,分别交AB于点A1,A2,…,An-2,An-1,则点A1,A2,…,An-2,An-1将线段AB分成n等份.题型一题型二题型三【变式训练1】 如图,已知线段AB,请用平行线等分线段定理将线段AB分成两部分,且两部分之比为2∶3.
解:已知:线段AB.
求作:线段AB上一点O,使AO∶OB=2∶3.
作法:(1)如图,作射线AC.
(2)在射线AC上以任意长顺次截取AD=DE=EF=FG=GH.
(3)连接BH.
(4)过点E作EO∥HB,交AB于点O,则点O为所求的点.题型一题型二题型三【例2】 如图,已知AC⊥AB,DB⊥AB,O是CD的中点.求证:OA=OB.
分析:因为线段OA和OB有共同端点,所以只需
证明点O在AB的垂直平分线上即可.
证明:过点O作AB的垂线,垂足为E,如图.
∵AC⊥AB,DB⊥AB,
∴OE∥AC∥DB.
∵O为CD的中点,
∴E为AB的中点.
又OE⊥AB,∴OA=OB.
反思证明两线段相等,往往借助于平行线等分线段定理,转化为证明其他线段相等.这种等价转化的思想要认真领会使用.题型一题型二题型三【变式训练2】 如图,已知在梯形ABCD中,AD∥BC,∠ABC=90°,M是CD的中点.求证:AM=BM.
证明:如图,过点M作ME∥BC交AB于点E,
∵AD∥BC,∴AD∥EM∥BC.
∵M是CD的中点,
∴E是AB的中点.
∵∠ABC=90°,
∴∠MEA=∠MEB=90°,
∴ME垂直平分AB.∴AM=BM.题型一题型二题型三【例3】 如图,在梯形ABCD中,AB∥DC,E为AD的中点,EF∥BC.求证:BC=2EF.
分析:由于EF∥BC,联系所证明的结果是BC=2EF,由此想到三角形中位线定理,过点A作BC的平行线即可证明.题型一题型二题型三证明:如图,过点A作BC的平行线AG,交DC于点G.
∵AB∥DC,
∴四边形ABCG是平行四边形.
∴AG??BC.
∵EF∥BC,∴EF∥AG.
∵E为AD的中点,∴F是DG的中点.
反思1.如果在三角形中出现中点,那么往往利用三角形中位线的性质来解决有关问题.
2.本题也可用平行线等分线段定理来证明,过点E作DC的平行线即可.题型一题型二题型三【变式训练3】 求证:顺次连接四边形四条边的中点,所得的四边形是平行四边形.
证明:已知:如图,在四边形ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
证明:连接AC.
∵AH=HD,DG=GC,
∴HG??EF.∴四边形EFGH是平行四边形.
2.能运用平行线等分线段定理任意等分已知线段,能运用推论进行简单的证明或计算.
3.会用三角形中位线定理解决问题.1231.平行线等分线段定理 123123名师点拨1.平行线等分线段定理的条件是a,b,c互相平行,构成一组平行线,m与n可以平行,也可以相交,但它们必须与已知的平行线a,b,c相交,即被平行线a,b,c所截.
2.平行线的条数可以多于3条,该定理还可以推广.123【做一做1】 如图,已知l1∥l2∥l3,直线a分别与l1,l2,l3相交于点A,B,C,且AB=BC,直线b分别与l1,l2,l3相交于点A1,B1,C1,则有( )
A.A1B1=B1C1
B.A1B1>B1C1
C.A1B1
解析:∵l1∥l2∥l3,AB=BC,根据平行线等分线段定理,
∴A1B1=B1C1.
答案:A1232.推论1 知识拓展三角形中位线的性质:三角形的中位线平行于第三边,并且等于第三边长的一半.123【做一做2】 如图,已知DE是△ABC的中位线,点F是BC上任一点,AF交DE于点G,则有( )
A.AG>GF
B.AG=GF
C.AG
解析:∵DE是△ABC的中位线,
∴在△ABF中,DG∥BF.
又AD=DB,
∴点G平分AF,即AG=GF.
答案:B1233.推论2
知识拓展梯形中位线的性质:梯形的中位线平行于两底边,并且等于两底边长和的一半.123【做一做3】 如图,已知在梯形ABCD中,AD∥BC,AD+BC=10 cm,E为AB的中点,点F在DC上,且EF∥AD,则EF的长为( )
A.5 cm
B.10 cm
C.20 cm
D.不确定
解析:由推论2知,EF是梯形ABCD的中位线,
答案:A平行线等分线段定理的两个推论的证明
剖析:(1)推论1,如图①,在△ABC中,B'为AB的中点,过点B'作B'C'∥BC交AC于点C',求证:点C'是AC的中点.证明:如图②,过点A作直线a∥BC,
∵BC∥B'C',∴a∥BC∥B'C'.
∵AB'=BB',∴AC'=CC',
即点C'是AC的中点.
(2)推论2,如图③,已知在梯形ACC'A'中,AA'∥CC',B是AC的中点,过点B作BB'∥CC'交A'C'于点B',求证:点B'是A'C'的中点.
证明:如图④,∵AA'∥CC',BB'∥CC',
∴AA'∥BB'∥CC'.
∵AB=BC,
∴A'B'=B'C',即点B'是A'C'的中点.题型一题型二题型三【例1】 如图,已知线段AB,求作线段AB的五等分点,并予以证明.
分析:利用平行线等分线段定理来作图.
作法:如图,(1)作射线AC;
(2)在射线AC上以任意取定的长度顺次截取AD1=D1D2=D2D3=D3D4=D4D5;
(3)连接D5B;
(4)分别过D1,D2,D3,D4作D5B的平行线D1A1,D2A2,D3A3,D4A4,分别交AB于点A1,A2,A3,A4,则点A1,A2,A3,A4将线段AB五等分.题型一题型二题型三证明:过点A作MN∥D5B.
则MN∥D4A4∥D3A3∥D2A2∥D1A1∥D5B.
∵AD1=D1D2=D2D3=D3D4=D4D5.
∴AA1=A1A2=A2A3=A3A4=A4B.
∴点A1,A2,A3,A4就是所求的线段AB的五等分点.
反思将已知线段AB分成n等份的解题步骤如下:
(1)作射线AC(与AB不共线);
(2)在射线AC上以任意取定的长度顺次截取AD1=D1D2=D2D3=…=Dn-1Dn;
(3)连接DnB;
(4)分别过点D1,D2,D3,…,Dn-2,Dn-1作DnB的平行线,分别交AB于点A1,A2,…,An-2,An-1,则点A1,A2,…,An-2,An-1将线段AB分成n等份.题型一题型二题型三【变式训练1】 如图,已知线段AB,请用平行线等分线段定理将线段AB分成两部分,且两部分之比为2∶3.
解:已知:线段AB.
求作:线段AB上一点O,使AO∶OB=2∶3.
作法:(1)如图,作射线AC.
(2)在射线AC上以任意长顺次截取AD=DE=EF=FG=GH.
(3)连接BH.
(4)过点E作EO∥HB,交AB于点O,则点O为所求的点.题型一题型二题型三【例2】 如图,已知AC⊥AB,DB⊥AB,O是CD的中点.求证:OA=OB.
分析:因为线段OA和OB有共同端点,所以只需
证明点O在AB的垂直平分线上即可.
证明:过点O作AB的垂线,垂足为E,如图.
∵AC⊥AB,DB⊥AB,
∴OE∥AC∥DB.
∵O为CD的中点,
∴E为AB的中点.
又OE⊥AB,∴OA=OB.
反思证明两线段相等,往往借助于平行线等分线段定理,转化为证明其他线段相等.这种等价转化的思想要认真领会使用.题型一题型二题型三【变式训练2】 如图,已知在梯形ABCD中,AD∥BC,∠ABC=90°,M是CD的中点.求证:AM=BM.
证明:如图,过点M作ME∥BC交AB于点E,
∵AD∥BC,∴AD∥EM∥BC.
∵M是CD的中点,
∴E是AB的中点.
∵∠ABC=90°,
∴∠MEA=∠MEB=90°,
∴ME垂直平分AB.∴AM=BM.题型一题型二题型三【例3】 如图,在梯形ABCD中,AB∥DC,E为AD的中点,EF∥BC.求证:BC=2EF.
分析:由于EF∥BC,联系所证明的结果是BC=2EF,由此想到三角形中位线定理,过点A作BC的平行线即可证明.题型一题型二题型三证明:如图,过点A作BC的平行线AG,交DC于点G.
∵AB∥DC,
∴四边形ABCG是平行四边形.
∴AG??BC.
∵EF∥BC,∴EF∥AG.
∵E为AD的中点,∴F是DG的中点.
反思1.如果在三角形中出现中点,那么往往利用三角形中位线的性质来解决有关问题.
2.本题也可用平行线等分线段定理来证明,过点E作DC的平行线即可.题型一题型二题型三【变式训练3】 求证:顺次连接四边形四条边的中点,所得的四边形是平行四边形.
证明:已知:如图,在四边形ABCD中,E,F,G,H分别为AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
证明:连接AC.
∵AH=HD,DG=GC,
∴HG??EF.∴四边形EFGH是平行四边形.
