高中数学新人教A版选修4-1课件:1.2平行线分线段成比例定理(26张)
文档属性
| 名称 | 高中数学新人教A版选修4-1课件:1.2平行线分线段成比例定理(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 919.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-24 17:00:16 | ||
图片预览





文档简介
课件26张PPT。二 平行线分线段成比例定理1.掌握平行线分线段成比例定理及其推论.
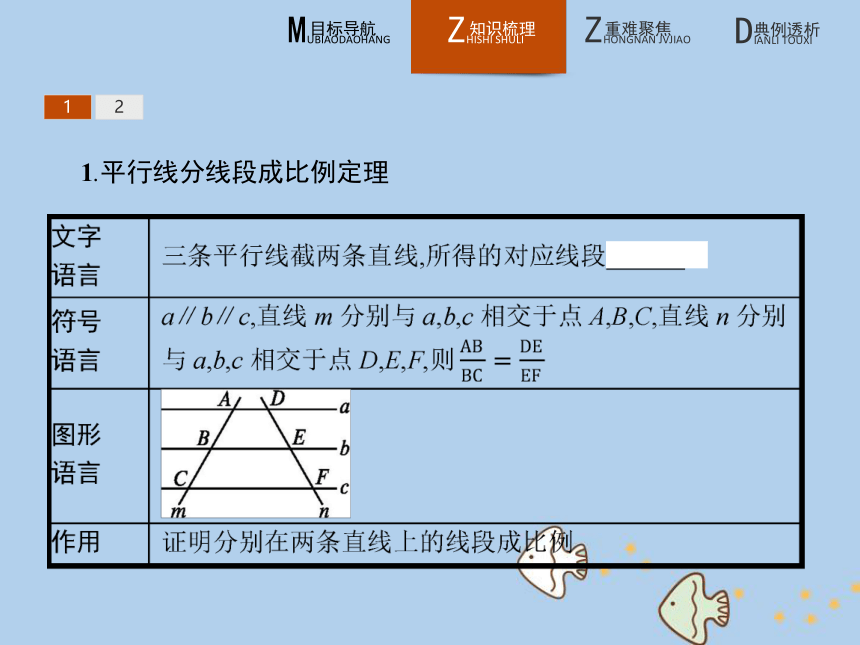
2.能利用平行线分线段成比例定理及推论解决有关问题.121.平行线分线段成比例定理 12名师点拨1.定理的条件与平行线等分线段定理的条件相同,它需要a,b,c互相平行,构成一组平行线,m与n可以平行,也可以相交,但它们必须与已知的平行线a,b,c相交,即被平行线a,b,c所截.平行线的条数还可以更多.
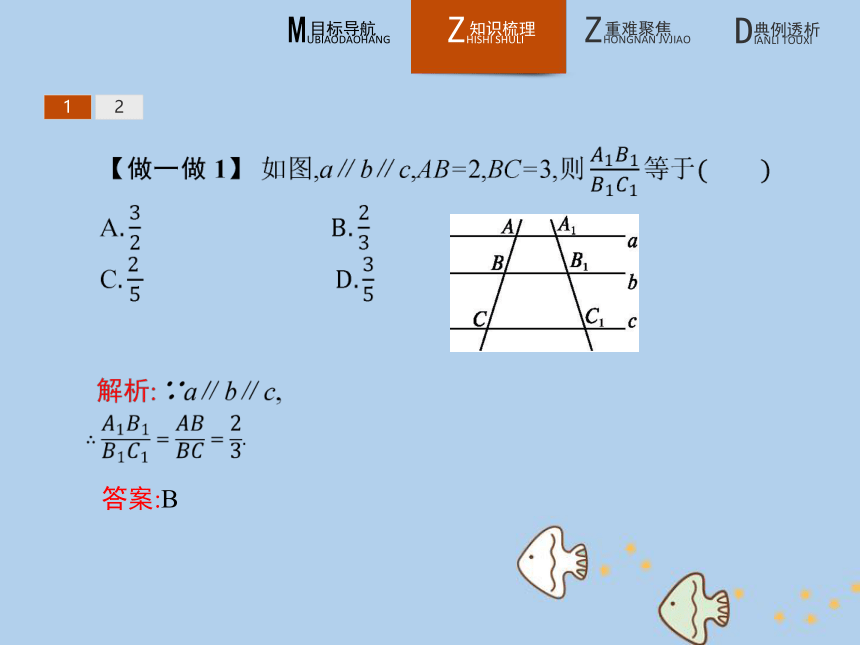
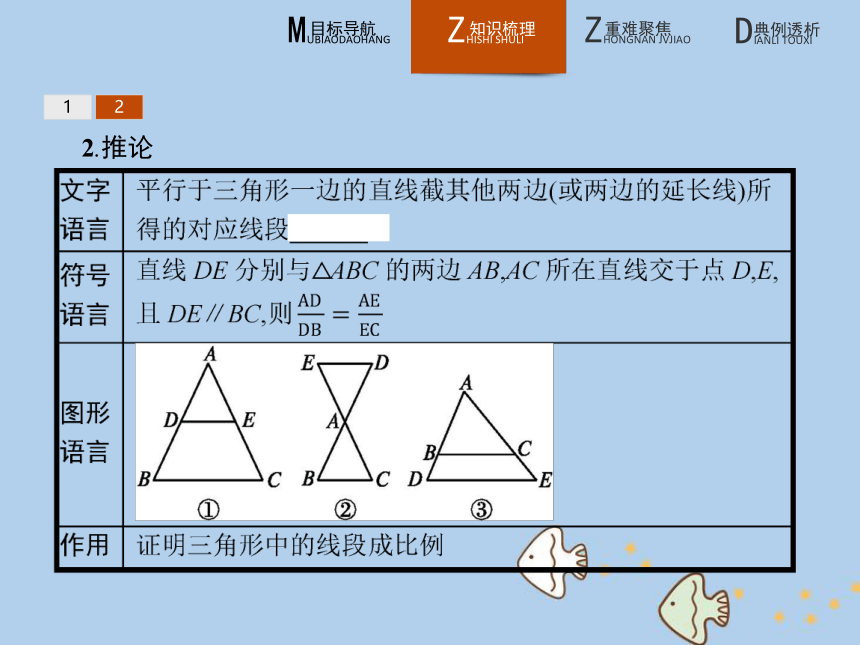
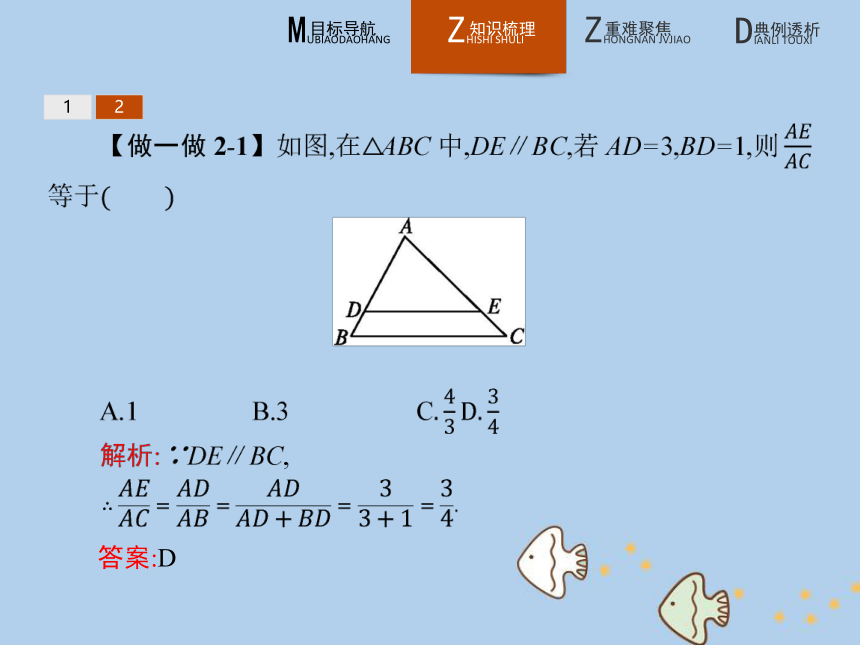
3.当截得的对应线段成比例,且比值为1时,则截得的线段相等,因此平行线分线段成比例定理是平行线等分线段定理的扩充,而平行线等分线段定理是平行线分线段成比例定理的特例;平行线等分线段定理是证明线段相等的依据,而平行线分线段成比例定理是证明线段成比例的依据.12答案:B 122.推论 12答案:D 12【做一做2-2】 如图,AB∥CD,AC,BD相交于O点,若BO=7,DO=3,AC=25,则AO的长为( )
A.10 B.12.5
C.15 D.17.5答案:D 比例的有关概念及性质
剖析:(1)线段的比:用同一个长度单位去量两条线段,所得的长度比叫做这两条线段的比.
(2)比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段.(5)线段的比与比例线段是既有区别又有联系的两个概念.线段的比是对两条线段而言的,而比例线段是对四条线段而言的.线段的比有顺序性,a∶b与b∶a通常是不相等的;比例线段也有顺序性,如线段a,b,c,d成比例与线段a,c,b,d成比例不同.题型一题型二题型三题型四【例1】 如图,AD为△ABC的中线,在AB上取点E,AC上取点F,使AE=AF.
分析:这道题目要证的比例中的线段都没有直接的联系,可以考虑把比例转移,过点C作CM∥EF,交AB于点M,交AD于点N,且BC的中点为D,可以考虑补出一个平行四边形来证明.题型一题型二题型三题型四证明:如图,过点C作CM∥EF,交AB于点M,交AD于点N.
∵AE=AF,∴AM=AC.
∵AD为△ABC的中线,∴BD=CD.
延长AD到点G,使得DG=AD,连接BG,CG,
则四边形ABGC为平行四边形.∴AB=GC.
又∵AB∥GC,AM=AC,GC=AB,题型一题型二题型三题型四反思1.比例线段常由平行线产生,因而研究比例线段问题应注意平行线的应用,在没有平行线时,可以添加平行线来促成比例线段的产生.
2.利用平行线产生比例或转移比例是常用的证题技巧,当题中没有平行线而有必要转移比例时,也常添加辅助平行线,从而达到转移比例的目的.题型一题型二题型三题型四【变式训练1】 如图,在△ABC(AB>AC)的边AB上取一点D,在边AC上取一点E,使AD=AE,直线DE和BC的延长线交于点P.
求证:BP∶CP=BD∶CE.题型一题型二题型三题型四题型一题型二题型三题型四反思在利用平行线证明或计算时,常常根据已知条件将复杂的图形进行分解,从中找出基本图形,“借图解题”.题型一题型二题型三题型四【变式训练2】 如图,在梯形ABCD中,AD∥BC,F为对角线AC上一点,FE∥BC交AB于点E,DF的延长线交BC于点H,DE的延长线交CB的延长线于点G.
求证:BC=GH.题型一题型二题型三题型四题型一题型二题型三题型四反思证明有关线段倒数和的等式时,常用的方法是首先将其变形为线段比的和为定值的形式,然后化归为同一直线上的线段比.题型一题型二题型三题型四【变式训练3】 如图,在梯形ABCD中,AD∥BC,EF经过梯形对角线的交点O,且EF∥AD.
(1)求证:OE=OF;题型一题型二题型三题型四题型一题型二题型三题型四【例4】 如图,M是?ABCD的边AB的中点,直线l过点M分别交AD,AC于点E,F,交CB的延长线于点N,若AE=2,AD=6.
求AF∶AC的值.
分析:AD∥BC,AM=MB?AE=BN?AF∶AC的值题型一题型二题型三题型四题型一题型二题型三题型四反思运用平行线分线段成比例定理及推论来计算比值,应分清相关三角形中的平行线段及所截的边,并注意在求解过程中运用比例的等比性质、合比性质等.题型一题型二题型三题型四题型一题型二题型三题型四
2.能利用平行线分线段成比例定理及推论解决有关问题.121.平行线分线段成比例定理 12名师点拨1.定理的条件与平行线等分线段定理的条件相同,它需要a,b,c互相平行,构成一组平行线,m与n可以平行,也可以相交,但它们必须与已知的平行线a,b,c相交,即被平行线a,b,c所截.平行线的条数还可以更多.
3.当截得的对应线段成比例,且比值为1时,则截得的线段相等,因此平行线分线段成比例定理是平行线等分线段定理的扩充,而平行线等分线段定理是平行线分线段成比例定理的特例;平行线等分线段定理是证明线段相等的依据,而平行线分线段成比例定理是证明线段成比例的依据.12答案:B 122.推论 12答案:D 12【做一做2-2】 如图,AB∥CD,AC,BD相交于O点,若BO=7,DO=3,AC=25,则AO的长为( )
A.10 B.12.5
C.15 D.17.5答案:D 比例的有关概念及性质
剖析:(1)线段的比:用同一个长度单位去量两条线段,所得的长度比叫做这两条线段的比.
(2)比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段.(5)线段的比与比例线段是既有区别又有联系的两个概念.线段的比是对两条线段而言的,而比例线段是对四条线段而言的.线段的比有顺序性,a∶b与b∶a通常是不相等的;比例线段也有顺序性,如线段a,b,c,d成比例与线段a,c,b,d成比例不同.题型一题型二题型三题型四【例1】 如图,AD为△ABC的中线,在AB上取点E,AC上取点F,使AE=AF.
分析:这道题目要证的比例中的线段都没有直接的联系,可以考虑把比例转移,过点C作CM∥EF,交AB于点M,交AD于点N,且BC的中点为D,可以考虑补出一个平行四边形来证明.题型一题型二题型三题型四证明:如图,过点C作CM∥EF,交AB于点M,交AD于点N.
∵AE=AF,∴AM=AC.
∵AD为△ABC的中线,∴BD=CD.
延长AD到点G,使得DG=AD,连接BG,CG,
则四边形ABGC为平行四边形.∴AB=GC.
又∵AB∥GC,AM=AC,GC=AB,题型一题型二题型三题型四反思1.比例线段常由平行线产生,因而研究比例线段问题应注意平行线的应用,在没有平行线时,可以添加平行线来促成比例线段的产生.
2.利用平行线产生比例或转移比例是常用的证题技巧,当题中没有平行线而有必要转移比例时,也常添加辅助平行线,从而达到转移比例的目的.题型一题型二题型三题型四【变式训练1】 如图,在△ABC(AB>AC)的边AB上取一点D,在边AC上取一点E,使AD=AE,直线DE和BC的延长线交于点P.
求证:BP∶CP=BD∶CE.题型一题型二题型三题型四题型一题型二题型三题型四反思在利用平行线证明或计算时,常常根据已知条件将复杂的图形进行分解,从中找出基本图形,“借图解题”.题型一题型二题型三题型四【变式训练2】 如图,在梯形ABCD中,AD∥BC,F为对角线AC上一点,FE∥BC交AB于点E,DF的延长线交BC于点H,DE的延长线交CB的延长线于点G.
求证:BC=GH.题型一题型二题型三题型四题型一题型二题型三题型四反思证明有关线段倒数和的等式时,常用的方法是首先将其变形为线段比的和为定值的形式,然后化归为同一直线上的线段比.题型一题型二题型三题型四【变式训练3】 如图,在梯形ABCD中,AD∥BC,EF经过梯形对角线的交点O,且EF∥AD.
(1)求证:OE=OF;题型一题型二题型三题型四题型一题型二题型三题型四【例4】 如图,M是?ABCD的边AB的中点,直线l过点M分别交AD,AC于点E,F,交CB的延长线于点N,若AE=2,AD=6.
求AF∶AC的值.
分析:AD∥BC,AM=MB?AE=BN?AF∶AC的值题型一题型二题型三题型四题型一题型二题型三题型四反思运用平行线分线段成比例定理及推论来计算比值,应分清相关三角形中的平行线段及所截的边,并注意在求解过程中运用比例的等比性质、合比性质等.题型一题型二题型三题型四题型一题型二题型三题型四
