高中数学新人教A版选修4-1课件:1.3.2相似三角形的性质(20张)
文档属性
| 名称 | 高中数学新人教A版选修4-1课件:1.3.2相似三角形的性质(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 495.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-24 00:00:00 | ||
图片预览








文档简介
课件20张PPT。2.相似三角形的性质1.掌握相似三角形的性质.
2.能利用相似三角形的性质解决有关问题.相似三角形的性质定理
(1)相似三角形对应角相等,对应边成比例;
(2)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比;
(3)相似三角形周长的比等于相似比;
(4)相似三角形面积的比等于相似比的平方;
(5)相似三角形外接(内切)圆的直径比、周长比等于相似比,外接(内切)圆的面积比等于相似比的平方.【做一做1】 已知△ABC∽△A'B'C',AB=4,A'B'=3,则BC和B'C'上对应中线的比等于( )
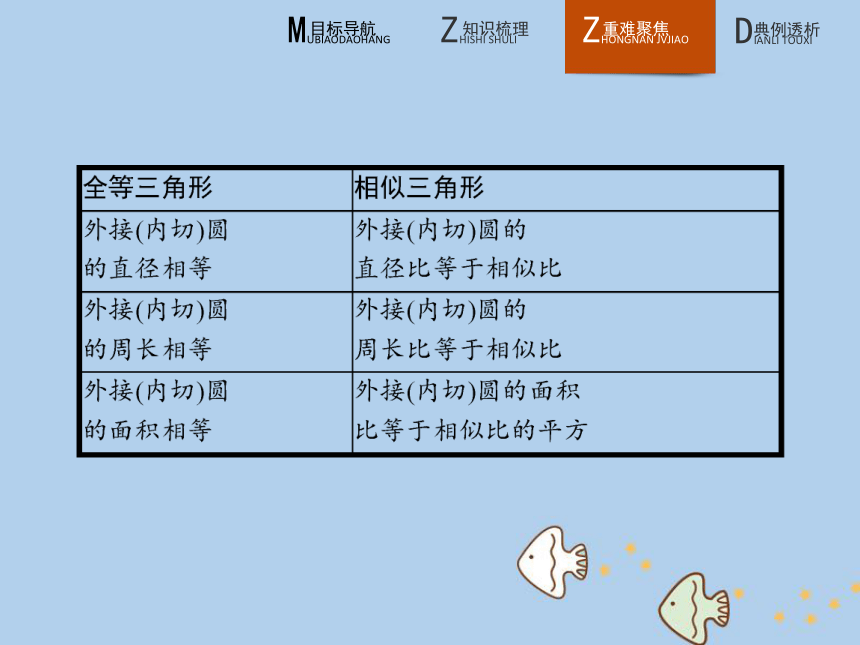
答案:A答案:B 答案:C 相似三角形性质和全等三角形性质的比较
剖析:如下表所示.题型一题型二题型三【例1】 已知△ABC∽△A'B'C',△ABC的周长为60 cm,△A'B'C'的周长为72 cm,AB=15 cm,B'C'=24 cm,求:
(1)BC,A'B'; (2)AC,A'C'.
分析:先由相似三角形周长的比得到相似比,再利用相似比求解.题型一题型二题型三题型一题型二题型三反思利用相似三角形的性质进行有关的计算,往往与相似三角形对应边的比及对应角相等有关.解决此类问题,要善于联想,变换比例式,从而达到求解的目的.题型一题型二题型三【变式训练1】 如果两个相似三角形对应边上的中线之比为3∶4,周长之和是35,那么这两个三角形的周长分别是 ( )
A.13和22 B.14和21
C.15和20 D.16和19
解析:由相似三角形的周长之比、对应中线之比均等于相似比,可得两个相似三角形的周长之比
又∵C1+C2=35,
∴C1=15,C2=20,即两个三角形的周长分别为15,20.
答案:C题型一题型二题型三分析:由于四边形BCDE是不规则四边形,直接求其面积有困难,因此可转化为求△ABC与△ADE的面积的差.题型一题型二题型三反思有关三角形的面积之比问题,除考虑三角形的相似比外,还要注意它们是否等高或等底,若是,则可转化为面积之比等于底边比或相应高之比.题型一题型二题型三【变式训练2】 如图,在△ABC中,DE∥BC,S△ADE∶S△ABC=4∶9.求:题型一题型二题型三题型一题型二题型三【例3】 如图,一天早上,小张正向着教学楼AB走去,教学楼后面有一水塔DC,可过了一会抬头一看:“怎么看不到水塔了?”小张心里很是纳闷.经过了解,教学楼、水塔的高分别是20 m和30 m,它们之间的距离为30 m,小张身高为1.6 m.小张要想看到水塔,他与教学楼之间的距离至少应有多少米?
分析:此题的解法很多,其关键是添加适当的辅助线,构造相似三角形,利用相似三角形的知识解题.题型一题型二题型三解:如图,设小张在点F与教学楼的距离为x m时,正好看到水塔.
连接FD,由题意知,点A在FD上,过F作FG⊥CD于点G,交AB于点H,则四边形FEBH、四边形BCGH都是矩形.
∵AB∥CD,∴△AFH∽△DFG.
∴AH∶DG=FH∶FG,
即(20-1.6)∶(30-1.6)=x∶(x+30),
解得x=55.2.
经检验x=55.2是所列方程的根.
故小张与教学楼的距离至少应有55.2 m,才能看到水塔.
反思此类问题是利用数学模型解决实际问题,关键在于认真分析题意转化成数学问题,构造相似三角形求解.题型一题型二题型三【变式训练3】 为了测量学校操场上旗杆的高度,小明请同学帮忙,测得同一时刻自己的影长和旗杆的影长分别为0.5 m和3 m,示意图如图.如果小明身高为1.5 m,那么旗杆的高度为 m.?题型一题型二题型三解析:根据题意,可得ED=0.5 m,DB=3 m,CD=1.5 m.
根据光线平行的知识可知CE∥AD,
故∠E=∠ADB.
∵AB⊥EB,CD⊥EB,
∴∠CDE=∠ABD=90°.
∴△ABD∽△CDE.
∴旗杆的高度为9 m.
答案:9
2.能利用相似三角形的性质解决有关问题.相似三角形的性质定理
(1)相似三角形对应角相等,对应边成比例;
(2)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比;
(3)相似三角形周长的比等于相似比;
(4)相似三角形面积的比等于相似比的平方;
(5)相似三角形外接(内切)圆的直径比、周长比等于相似比,外接(内切)圆的面积比等于相似比的平方.【做一做1】 已知△ABC∽△A'B'C',AB=4,A'B'=3,则BC和B'C'上对应中线的比等于( )
答案:A答案:B 答案:C 相似三角形性质和全等三角形性质的比较
剖析:如下表所示.题型一题型二题型三【例1】 已知△ABC∽△A'B'C',△ABC的周长为60 cm,△A'B'C'的周长为72 cm,AB=15 cm,B'C'=24 cm,求:
(1)BC,A'B'; (2)AC,A'C'.
分析:先由相似三角形周长的比得到相似比,再利用相似比求解.题型一题型二题型三题型一题型二题型三反思利用相似三角形的性质进行有关的计算,往往与相似三角形对应边的比及对应角相等有关.解决此类问题,要善于联想,变换比例式,从而达到求解的目的.题型一题型二题型三【变式训练1】 如果两个相似三角形对应边上的中线之比为3∶4,周长之和是35,那么这两个三角形的周长分别是 ( )
A.13和22 B.14和21
C.15和20 D.16和19
解析:由相似三角形的周长之比、对应中线之比均等于相似比,可得两个相似三角形的周长之比
又∵C1+C2=35,
∴C1=15,C2=20,即两个三角形的周长分别为15,20.
答案:C题型一题型二题型三分析:由于四边形BCDE是不规则四边形,直接求其面积有困难,因此可转化为求△ABC与△ADE的面积的差.题型一题型二题型三反思有关三角形的面积之比问题,除考虑三角形的相似比外,还要注意它们是否等高或等底,若是,则可转化为面积之比等于底边比或相应高之比.题型一题型二题型三【变式训练2】 如图,在△ABC中,DE∥BC,S△ADE∶S△ABC=4∶9.求:题型一题型二题型三题型一题型二题型三【例3】 如图,一天早上,小张正向着教学楼AB走去,教学楼后面有一水塔DC,可过了一会抬头一看:“怎么看不到水塔了?”小张心里很是纳闷.经过了解,教学楼、水塔的高分别是20 m和30 m,它们之间的距离为30 m,小张身高为1.6 m.小张要想看到水塔,他与教学楼之间的距离至少应有多少米?
分析:此题的解法很多,其关键是添加适当的辅助线,构造相似三角形,利用相似三角形的知识解题.题型一题型二题型三解:如图,设小张在点F与教学楼的距离为x m时,正好看到水塔.
连接FD,由题意知,点A在FD上,过F作FG⊥CD于点G,交AB于点H,则四边形FEBH、四边形BCGH都是矩形.
∵AB∥CD,∴△AFH∽△DFG.
∴AH∶DG=FH∶FG,
即(20-1.6)∶(30-1.6)=x∶(x+30),
解得x=55.2.
经检验x=55.2是所列方程的根.
故小张与教学楼的距离至少应有55.2 m,才能看到水塔.
反思此类问题是利用数学模型解决实际问题,关键在于认真分析题意转化成数学问题,构造相似三角形求解.题型一题型二题型三【变式训练3】 为了测量学校操场上旗杆的高度,小明请同学帮忙,测得同一时刻自己的影长和旗杆的影长分别为0.5 m和3 m,示意图如图.如果小明身高为1.5 m,那么旗杆的高度为 m.?题型一题型二题型三解析:根据题意,可得ED=0.5 m,DB=3 m,CD=1.5 m.
根据光线平行的知识可知CE∥AD,
故∠E=∠ADB.
∵AB⊥EB,CD⊥EB,
∴∠CDE=∠ABD=90°.
∴△ABD∽△CDE.
∴旗杆的高度为9 m.
答案:9
