高中数学新人教A版选修4-1课件:1.4直角三角形的射影定理(17张)
文档属性
| 名称 | 高中数学新人教A版选修4-1课件:1.4直角三角形的射影定理(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 456.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 09:40:18 | ||
图片预览




文档简介
课件17张PPT。四 直角三角形的射影定理1.掌握正射影即射影的概念,能画出点和线段的射影.
2.理解并掌握射影定理,并能解决有关问题.121.射影
从一点向一条直线所引垂线的垂足,叫做这个点在这条直线上的正射影.一条线段的两个端点在一条直线上的正射影之间的线段,叫做这条线段在这条直线上的正射影.点和线段的正射影简称为射影.
【做一做1】 线段MN在直线l上的射影不可能是 ( )
A.点 B.线段
C.与MN等长的线段 D.直线
解析:当MN⊥l时,射影是一个点;当MN与l不垂直时,射影是一条线段;特别地,当MN∥l或MN在l上时,射影与MN等长,线段MN的射影不可能是直线.
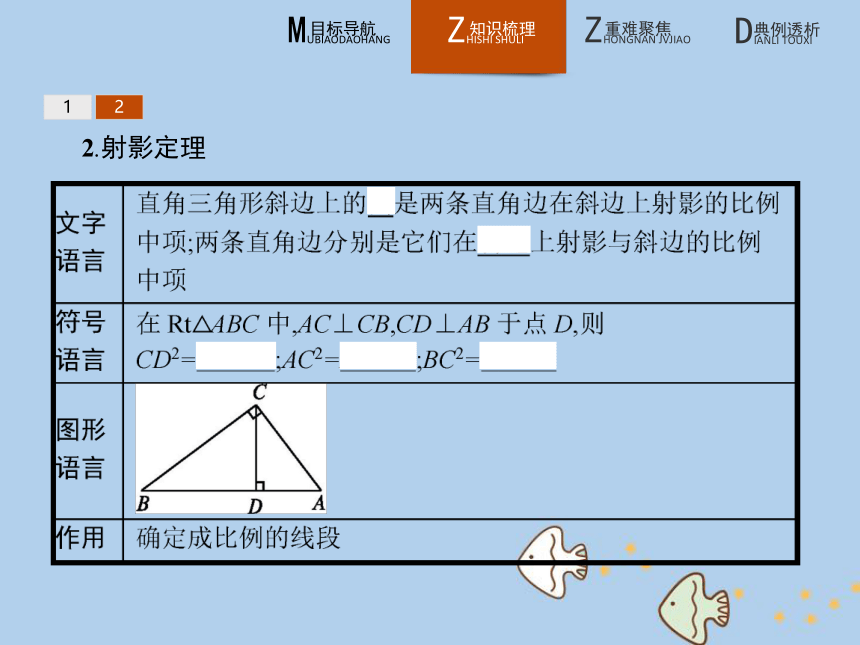
答案:D122.射影定理 12名师点拨
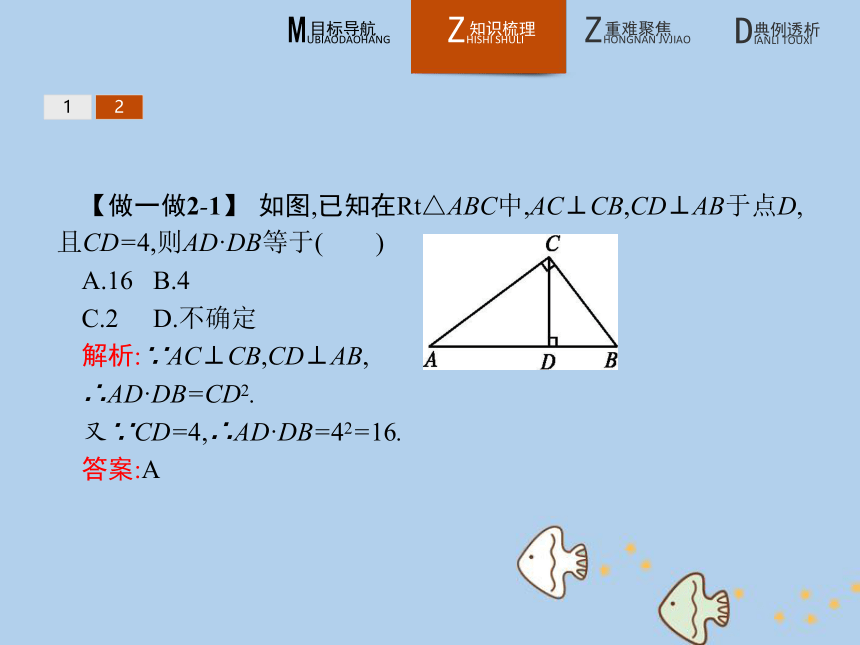
1.勾股定理:AC2+BC2=AB2,AD2+CD2=AC2,BD2+CD2=BC2.12【做一做2-1】 如图,已知在Rt△ABC中,AC⊥CB,CD⊥AB于点D,且CD=4,则AD·DB等于( )
A.16 B.4
C.2 D.不确定
解析:∵AC⊥CB,CD⊥AB,
∴AD·DB=CD2.
又∵CD=4,∴AD·DB=42=16.
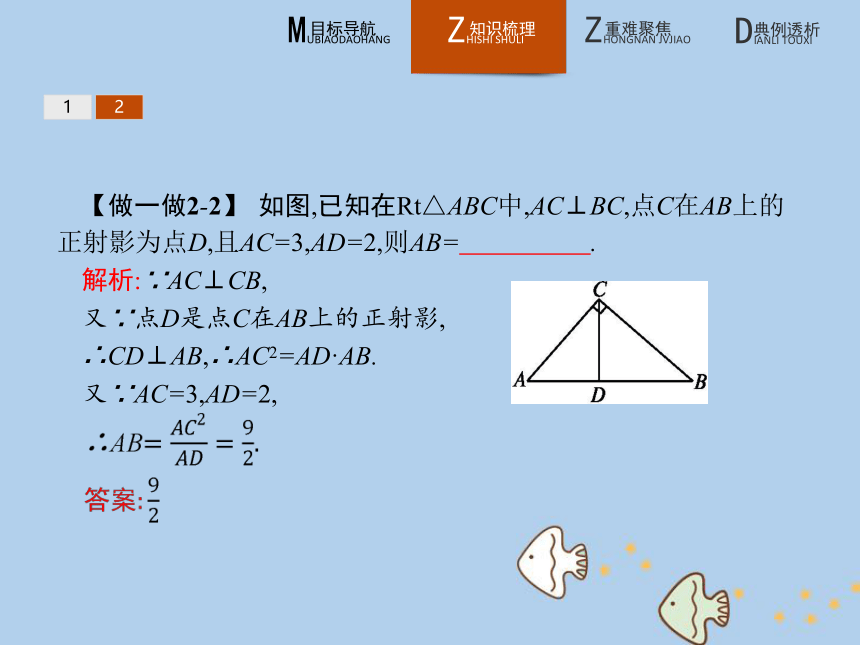
答案:A12【做一做2-2】 如图,已知在Rt△ABC中,AC⊥BC,点C在AB上的正射影为点D,且AC=3,AD=2,则AB= .?
解析:∵AC⊥CB,
又∵点D是点C在AB上的正射影,
∴CD⊥AB,∴AC2=AD·AB.
又∵AC=3,AD=2,用射影定理证明勾股定理
剖析:如图,在Rt△ABC中,AC⊥CB,CD⊥AB于点D,则由射影定理可得AC2=AD·AB,BC2=BD·BA,
则AC2+BC2=AD·AB+BD·BA=(AD+BD)·AB=AB2,即AC2+BC2=AB2.
由此可见,利用射影定理可以证明勾股定理.过去我们是用面积割补的方法证明勾股定理的,现在我们又用射影定理证明了勾股定理,而且这种方法简洁明快,比用面积割补的方法要方便得多.题型一题型二题型三【例1】 若CD是Rt△ACB斜边AB上的高,AB=25,AC=20,试确定DB和CD的长.
分析:先用射影定理求出AD,从而求出DB,再用
射影定理求出CD.
解:∵AC⊥CB,CD⊥AB,
∴AC2=AD·AB,CD2=AD·DB.题型一题型二题型三反思1.本题可先用勾股定理求出BC,再用射影定理求出BD,最后用勾股定理求出CD;此外还有其他方法.
2.运用射影定理进行直角三角形中的相关计算,有时需要与直角三角形的其他性质相结合来解.如本题中,直角三角形中的六条线段AC,BC,CD,AD,DB,AB,若已知其中任意两条线段的长,就可以计算出其余线段的长.题型一题型二题型三【变式训练1】 如图,在Rt△ABC中,CD为斜边AB上的高.若AD=2 cm,DB=6 cm,求CD,AC,BC的长.
解:∵AC⊥CB,CD⊥AB,
∴CD2=AD·DB=2×6=12,题型一题型二题型三【例2】 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC交AC于点E,EF⊥BC于点F.求证:EF∶DF=BC∶AC.题型一题型二题型三反思利用射影定理证明比例式成立的证明问题在本部分中比较常见,在解题过程中,应弄清射影定理中成比例的线段,再结合比例的基本性质加以灵活运用.题型一题型二题型三题型一题型二题型三题型一题型二题型三易错点:射影定理记忆不牢而致错
【例3】 在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,若BD∶AD=1∶9,则tan∠BCD= .?
错解:在Rt△ACB中,设BD=x,则AD=9x,
又∵CD2=AD·AB,
错因分析:本题的错因是没有准确地记住射影定理中的三组公式,误认为CD2=AD·AB致误.题型一题型二题型三正解:在Rt△ACB中,CD⊥AB,由射影定理得CD2=AD·BD.
又BD∶AD=1∶9,令BD=x,
则AD=9x(x>0).
∴CD2=9x2.
∴CD=3x.
2.理解并掌握射影定理,并能解决有关问题.121.射影
从一点向一条直线所引垂线的垂足,叫做这个点在这条直线上的正射影.一条线段的两个端点在一条直线上的正射影之间的线段,叫做这条线段在这条直线上的正射影.点和线段的正射影简称为射影.
【做一做1】 线段MN在直线l上的射影不可能是 ( )
A.点 B.线段
C.与MN等长的线段 D.直线
解析:当MN⊥l时,射影是一个点;当MN与l不垂直时,射影是一条线段;特别地,当MN∥l或MN在l上时,射影与MN等长,线段MN的射影不可能是直线.
答案:D122.射影定理 12名师点拨
1.勾股定理:AC2+BC2=AB2,AD2+CD2=AC2,BD2+CD2=BC2.12【做一做2-1】 如图,已知在Rt△ABC中,AC⊥CB,CD⊥AB于点D,且CD=4,则AD·DB等于( )
A.16 B.4
C.2 D.不确定
解析:∵AC⊥CB,CD⊥AB,
∴AD·DB=CD2.
又∵CD=4,∴AD·DB=42=16.
答案:A12【做一做2-2】 如图,已知在Rt△ABC中,AC⊥BC,点C在AB上的正射影为点D,且AC=3,AD=2,则AB= .?
解析:∵AC⊥CB,
又∵点D是点C在AB上的正射影,
∴CD⊥AB,∴AC2=AD·AB.
又∵AC=3,AD=2,用射影定理证明勾股定理
剖析:如图,在Rt△ABC中,AC⊥CB,CD⊥AB于点D,则由射影定理可得AC2=AD·AB,BC2=BD·BA,
则AC2+BC2=AD·AB+BD·BA=(AD+BD)·AB=AB2,即AC2+BC2=AB2.
由此可见,利用射影定理可以证明勾股定理.过去我们是用面积割补的方法证明勾股定理的,现在我们又用射影定理证明了勾股定理,而且这种方法简洁明快,比用面积割补的方法要方便得多.题型一题型二题型三【例1】 若CD是Rt△ACB斜边AB上的高,AB=25,AC=20,试确定DB和CD的长.
分析:先用射影定理求出AD,从而求出DB,再用
射影定理求出CD.
解:∵AC⊥CB,CD⊥AB,
∴AC2=AD·AB,CD2=AD·DB.题型一题型二题型三反思1.本题可先用勾股定理求出BC,再用射影定理求出BD,最后用勾股定理求出CD;此外还有其他方法.
2.运用射影定理进行直角三角形中的相关计算,有时需要与直角三角形的其他性质相结合来解.如本题中,直角三角形中的六条线段AC,BC,CD,AD,DB,AB,若已知其中任意两条线段的长,就可以计算出其余线段的长.题型一题型二题型三【变式训练1】 如图,在Rt△ABC中,CD为斜边AB上的高.若AD=2 cm,DB=6 cm,求CD,AC,BC的长.
解:∵AC⊥CB,CD⊥AB,
∴CD2=AD·DB=2×6=12,题型一题型二题型三【例2】 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC交AC于点E,EF⊥BC于点F.求证:EF∶DF=BC∶AC.题型一题型二题型三反思利用射影定理证明比例式成立的证明问题在本部分中比较常见,在解题过程中,应弄清射影定理中成比例的线段,再结合比例的基本性质加以灵活运用.题型一题型二题型三题型一题型二题型三题型一题型二题型三易错点:射影定理记忆不牢而致错
【例3】 在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,若BD∶AD=1∶9,则tan∠BCD= .?
错解:在Rt△ACB中,设BD=x,则AD=9x,
又∵CD2=AD·AB,
错因分析:本题的错因是没有准确地记住射影定理中的三组公式,误认为CD2=AD·AB致误.题型一题型二题型三正解:在Rt△ACB中,CD⊥AB,由射影定理得CD2=AD·BD.
又BD∶AD=1∶9,令BD=x,
则AD=9x(x>0).
∴CD2=9x2.
∴CD=3x.
