高中数学新人教A版选修4-1课件:2.2圆内接四边形的性质与判定定理(25张)
文档属性
| 名称 | 高中数学新人教A版选修4-1课件:2.2圆内接四边形的性质与判定定理(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 598.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 00:00:00 | ||
图片预览




文档简介
课件25张PPT。二 圆内接四边形的性质与判定定理1.了解圆内接四边形的概念,掌握圆内接四边形的性质定理及其应用.
2.理解圆内接四边形的判定定理及其推论,并能解决有关问题.
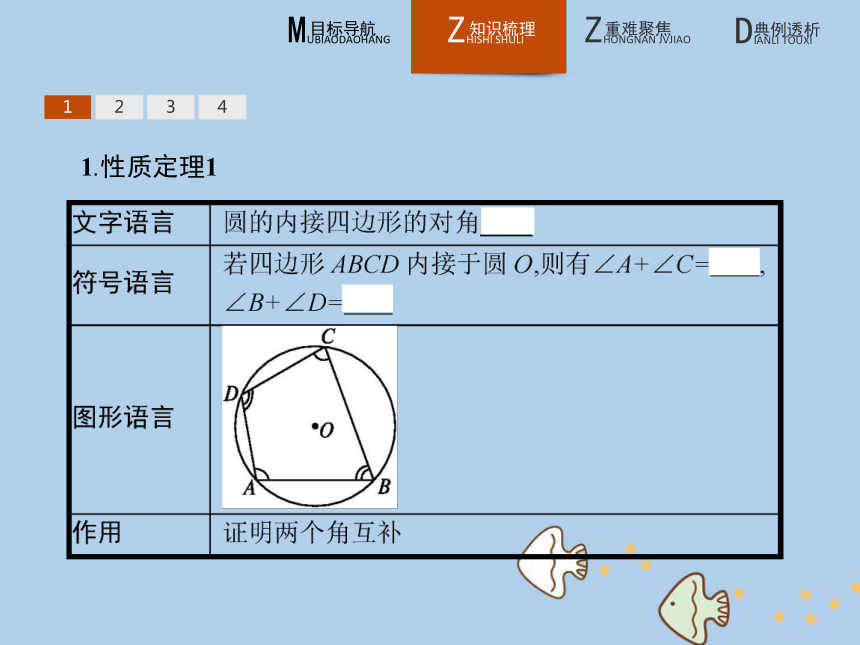
3.了解反证法在证明问题中的应用.12341.性质定理1 1234【做一做1】 已知四边形ABCD内接于圆O,∠A=25°,则∠C等于( )
A.25° B.75° C.115° D.155°
解析:∵四边形ABCD内接于圆,
∴∠A+∠C=180°.
又∵∠A=25°,
∴∠C=180°-∠A=155°.
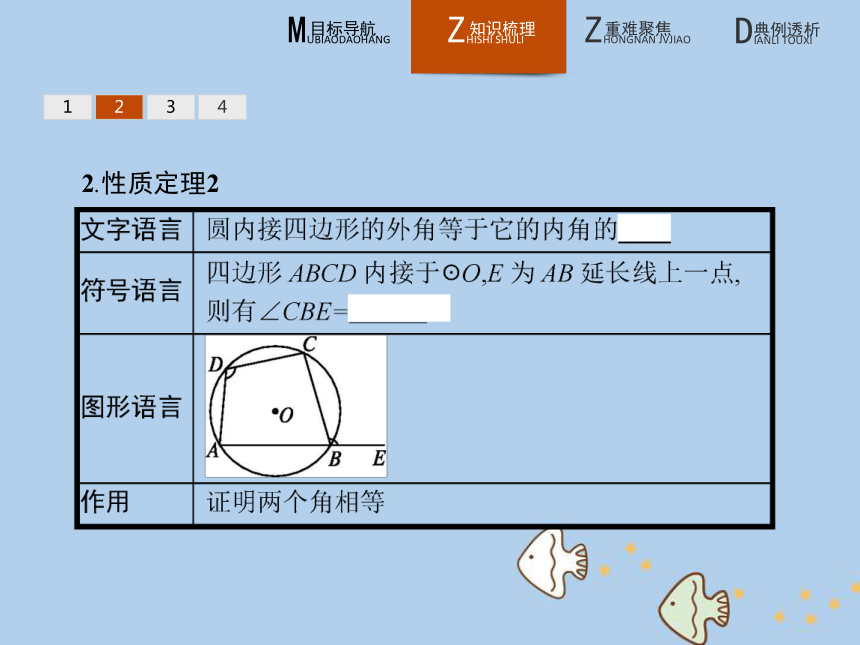
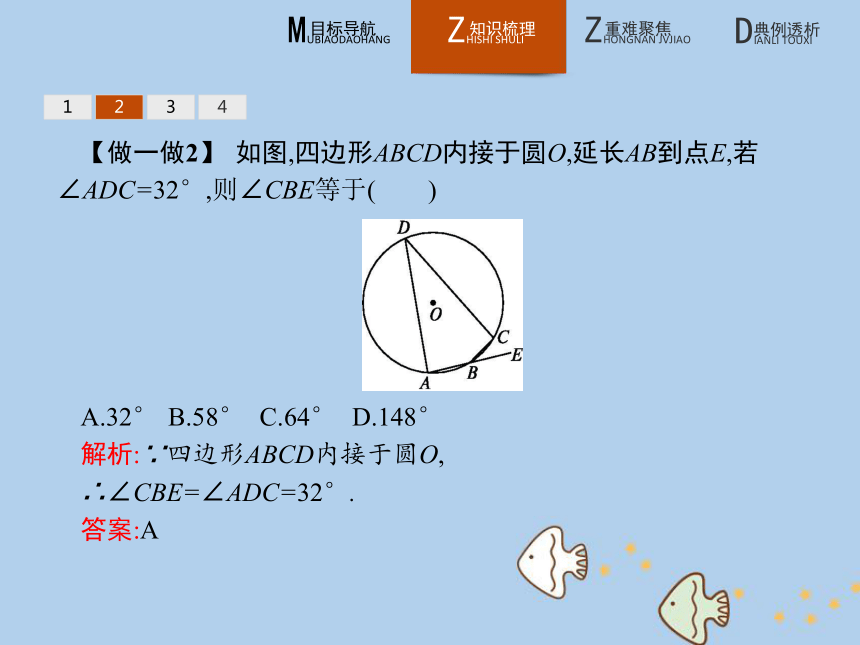
答案:D12342.性质定理2 1234【做一做2】 如图,四边形ABCD内接于圆O,延长AB到点E,若∠ADC=32°,则∠CBE等于( )
A.32° B.58° C.64° D.148°
解析:∵四边形ABCD内接于圆O,
∴∠CBE=∠ADC=32°.
答案:A1234归纳总结1.利用这两个性质定理,可以借助圆变换角的位置,得到角的相等关系或互补关系,再进行其他的计算或证明.
2.利用这两个定理可以得出一些重要结论,如内接于圆的平行四边形是矩形;内接于圆的菱形是正方形;内接于圆的梯形是等腰梯形等.12343.圆内接四边形判定定理 1234【做一做3】 下列四边形的四个顶点共圆的是( )
A.梯形 B.矩形
C.平行四边形 D.菱形
答案:B 12434.推论 归纳总结性质定理1和判定定理互为逆定理,性质定理2和判定定理的推论互为逆定理.1243【做一做4】 如图,四边形ABCD的边AB的延长线上有一点E,且BC=BE,∠D=80°,∠E=50°.求证:四边形ABCD内接于圆.
证明:∵BC=BE,∴∠E=∠BCE.
则∠EBC=180°-2∠E=80°,
∴∠EBC=∠D.∴四边形ABCD内接于圆.1.圆内接四边形的性质定理与判定定理
剖析:(1)圆的内接四边形的外角及内对角
如图,圆内接四边形ABCD的内角∠BAD的两个补角∠1和∠2称为圆内接四边形的外角.因为∠BAD和∠C两角相对,所以∠C称为∠1与∠2的内对角,且它们满足∠BAD+∠C=180°,∠1=∠2=∠C.
(2)判定定理与性质定理的内在联系
性质定理1和判定定理互为逆定理,性质定理2与判定定理的推论互为逆定理.2.与圆内接四边形有关的相似三角形
剖析:如图,通过掌握与圆有关的相似三角形的基本图形,可以在解题过程中遵循正确的思维规律和解题步骤,对图形运用自如,融为一体,做出连贯反应.
基本图形1 基本图形2 基本图形3基本图形1:圆的任意内接四边形ABCD,有△AED∽△BEC,△DEC∽△AEB.
基本图形2:四边形ABCD内接于☉O,AD,BC的延长线交于点F,其中相似三角形有△AED∽△BEC,△AEB∽△DEC,△CDF∽△ABF,△ACF∽△BDF.
基本图形3:四边形ABCD内接于☉O,AD,BC的延长线交于点F,AB为直径,其中相似三角形有△DEC∽△AEB,△FDC∽△FBA,Rt△AFC∽Rt△BFD∽Rt△AED∽Rt△BEC.题型一题型二题型三【例1】 如图,在△ABC中,E,D,F分别为AB,BC,AC的中点,且AP⊥BC于点P.求证:E,D,P,F四点共圆.
分析:连接PF,转化为证明∠FED=∠FPC,先利用中点证明∠FED=∠C,再利用AP⊥BC证明PF=FC,得∠C=∠FPC,即得出∠FED=∠FPC.题型一题型二题型三证明:如图,连接PF.
∵AP⊥BC,F为AC的中点,
∴PF是Rt△APC斜边上的中线.
∴PF=FC,∴∠FPC=∠C.
∵E,F,D分别为AB,AC,BC的中点,
∴EF∥CD,ED∥FC.
∴四边形EDCF为平行四边形.
∴∠FED=∠C,∴∠FPC=∠FED.
∴E,D,P,F四点共圆. 题型一题型二题型三反思判定四点共圆的方法:①如果四个点与一定点距离相等,那么这四个点共圆;②如果一个四边形的一组对角互补,那么这个四边形的四个顶点共圆;③如果一个四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆(如本题);④与线段两个端点连线的夹角相等(或互补)的点连同该线段两个端点在内共圆.题型一题型二题型三【变式训练1】 在锐角三角形ABC中,AD是BC边上的高,DE⊥AB,DF⊥AC,点E,F是垂足.
求证:E,B,C,F四点共圆.题型一题型二题型三证明:如图,连接EF,
∵DE⊥AB,DF⊥AC,
∴A,E,D,F四点共圆.
∴∠1=∠2.
∵AD是BC边上的高,
∴∠1+∠C=∠2+∠C=90°.
∴∠BEF+∠C=180°.
∴B,E,F,C四点共圆.题型一题型二题型三【例2】 如图,已知四边形ABCD内接于☉O,延长AB和DC相交于点E,EG平分∠AED,且与BC,AD分别交于点F,G.求证:∠CFG=∠DGF.
分析:由∠BEF=∠DEG,可证明△EBF∽△EDG,又∠BFE与∠CFG是对顶角,问题获证.题型一题型二题型三证明:∵四边形ABCD内接于☉O,
∴∠EBF=∠ADE.
又EF是∠AED的平分线,
则∠BEF=∠DEG,
∴△EBF∽△EDG.
∴∠EFB=∠DGF.
又∵∠EFB=∠CFG,
∴∠CFG=∠DGF.
反思当已知条件中出现圆内接四边形时,常用圆内接四边形的性质定理来获得角相等或互补,从而为证明三角形相似或两条直线平行等问题创造条件.题型一题型二题型三【变式训练2】 如图,两圆☉O1,☉O2相交于点A,B.☉O1的弦BC交☉O2于点E,☉O2的弦BD交☉O1于点F.
求证:(1)若∠DBA=∠CBA,则DF=CE;
(2)若DF=CE,则∠DBA=∠CBA.题型一题型二题型三证明:(1)如图,连接AE,AF,AC,AD,则∠3=∠4,∠5=∠6.
∴AD=AE,∴△ACE≌△AFD.
故CE=DF.
(2)由(1)得∠3=∠4,∠5=∠6.
又∵DF=CE,∴△ACE≌△AFD,
∴AD=AE,
∴∠1=∠2,即∠DBA=∠CBA.题型一题型二题型三易错点:错用圆内接四边形的外角等于它的内角的对角这一定理而致错【例3】 如图,四边形ABCD是☉O的内接四边形,E为AB的延长线上一点,若∠CBE=40°,则∠AOC等于( )
A.20° B.40°
C.80° D.100°
错解:∵四边形ABCD是☉O的内接四边形,
∴根据圆内接四边形的外角等于它的内角的对角,得∠CBE=∠COA=40°.故选B.
错因分析:上述解答错误的原因是对性质定理2的理解不透彻,不能准确理解“外角等于它的内角的对角”的含义.所谓的“内角的对角”通常是指圆周角.题型一题型二题型三正解:∵四边形ABCD是圆内接四边形,且∠CBE=40°,由圆内接四边形的性质知∠D=∠CBE=40°.又由圆周角定理知∠AOC=2∠D=80°.
答案:C
2.理解圆内接四边形的判定定理及其推论,并能解决有关问题.
3.了解反证法在证明问题中的应用.12341.性质定理1 1234【做一做1】 已知四边形ABCD内接于圆O,∠A=25°,则∠C等于( )
A.25° B.75° C.115° D.155°
解析:∵四边形ABCD内接于圆,
∴∠A+∠C=180°.
又∵∠A=25°,
∴∠C=180°-∠A=155°.
答案:D12342.性质定理2 1234【做一做2】 如图,四边形ABCD内接于圆O,延长AB到点E,若∠ADC=32°,则∠CBE等于( )
A.32° B.58° C.64° D.148°
解析:∵四边形ABCD内接于圆O,
∴∠CBE=∠ADC=32°.
答案:A1234归纳总结1.利用这两个性质定理,可以借助圆变换角的位置,得到角的相等关系或互补关系,再进行其他的计算或证明.
2.利用这两个定理可以得出一些重要结论,如内接于圆的平行四边形是矩形;内接于圆的菱形是正方形;内接于圆的梯形是等腰梯形等.12343.圆内接四边形判定定理 1234【做一做3】 下列四边形的四个顶点共圆的是( )
A.梯形 B.矩形
C.平行四边形 D.菱形
答案:B 12434.推论 归纳总结性质定理1和判定定理互为逆定理,性质定理2和判定定理的推论互为逆定理.1243【做一做4】 如图,四边形ABCD的边AB的延长线上有一点E,且BC=BE,∠D=80°,∠E=50°.求证:四边形ABCD内接于圆.
证明:∵BC=BE,∴∠E=∠BCE.
则∠EBC=180°-2∠E=80°,
∴∠EBC=∠D.∴四边形ABCD内接于圆.1.圆内接四边形的性质定理与判定定理
剖析:(1)圆的内接四边形的外角及内对角
如图,圆内接四边形ABCD的内角∠BAD的两个补角∠1和∠2称为圆内接四边形的外角.因为∠BAD和∠C两角相对,所以∠C称为∠1与∠2的内对角,且它们满足∠BAD+∠C=180°,∠1=∠2=∠C.
(2)判定定理与性质定理的内在联系
性质定理1和判定定理互为逆定理,性质定理2与判定定理的推论互为逆定理.2.与圆内接四边形有关的相似三角形
剖析:如图,通过掌握与圆有关的相似三角形的基本图形,可以在解题过程中遵循正确的思维规律和解题步骤,对图形运用自如,融为一体,做出连贯反应.
基本图形1 基本图形2 基本图形3基本图形1:圆的任意内接四边形ABCD,有△AED∽△BEC,△DEC∽△AEB.
基本图形2:四边形ABCD内接于☉O,AD,BC的延长线交于点F,其中相似三角形有△AED∽△BEC,△AEB∽△DEC,△CDF∽△ABF,△ACF∽△BDF.
基本图形3:四边形ABCD内接于☉O,AD,BC的延长线交于点F,AB为直径,其中相似三角形有△DEC∽△AEB,△FDC∽△FBA,Rt△AFC∽Rt△BFD∽Rt△AED∽Rt△BEC.题型一题型二题型三【例1】 如图,在△ABC中,E,D,F分别为AB,BC,AC的中点,且AP⊥BC于点P.求证:E,D,P,F四点共圆.
分析:连接PF,转化为证明∠FED=∠FPC,先利用中点证明∠FED=∠C,再利用AP⊥BC证明PF=FC,得∠C=∠FPC,即得出∠FED=∠FPC.题型一题型二题型三证明:如图,连接PF.
∵AP⊥BC,F为AC的中点,
∴PF是Rt△APC斜边上的中线.
∴PF=FC,∴∠FPC=∠C.
∵E,F,D分别为AB,AC,BC的中点,
∴EF∥CD,ED∥FC.
∴四边形EDCF为平行四边形.
∴∠FED=∠C,∴∠FPC=∠FED.
∴E,D,P,F四点共圆. 题型一题型二题型三反思判定四点共圆的方法:①如果四个点与一定点距离相等,那么这四个点共圆;②如果一个四边形的一组对角互补,那么这个四边形的四个顶点共圆;③如果一个四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆(如本题);④与线段两个端点连线的夹角相等(或互补)的点连同该线段两个端点在内共圆.题型一题型二题型三【变式训练1】 在锐角三角形ABC中,AD是BC边上的高,DE⊥AB,DF⊥AC,点E,F是垂足.
求证:E,B,C,F四点共圆.题型一题型二题型三证明:如图,连接EF,
∵DE⊥AB,DF⊥AC,
∴A,E,D,F四点共圆.
∴∠1=∠2.
∵AD是BC边上的高,
∴∠1+∠C=∠2+∠C=90°.
∴∠BEF+∠C=180°.
∴B,E,F,C四点共圆.题型一题型二题型三【例2】 如图,已知四边形ABCD内接于☉O,延长AB和DC相交于点E,EG平分∠AED,且与BC,AD分别交于点F,G.求证:∠CFG=∠DGF.
分析:由∠BEF=∠DEG,可证明△EBF∽△EDG,又∠BFE与∠CFG是对顶角,问题获证.题型一题型二题型三证明:∵四边形ABCD内接于☉O,
∴∠EBF=∠ADE.
又EF是∠AED的平分线,
则∠BEF=∠DEG,
∴△EBF∽△EDG.
∴∠EFB=∠DGF.
又∵∠EFB=∠CFG,
∴∠CFG=∠DGF.
反思当已知条件中出现圆内接四边形时,常用圆内接四边形的性质定理来获得角相等或互补,从而为证明三角形相似或两条直线平行等问题创造条件.题型一题型二题型三【变式训练2】 如图,两圆☉O1,☉O2相交于点A,B.☉O1的弦BC交☉O2于点E,☉O2的弦BD交☉O1于点F.
求证:(1)若∠DBA=∠CBA,则DF=CE;
(2)若DF=CE,则∠DBA=∠CBA.题型一题型二题型三证明:(1)如图,连接AE,AF,AC,AD,则∠3=∠4,∠5=∠6.
∴AD=AE,∴△ACE≌△AFD.
故CE=DF.
(2)由(1)得∠3=∠4,∠5=∠6.
又∵DF=CE,∴△ACE≌△AFD,
∴AD=AE,
∴∠1=∠2,即∠DBA=∠CBA.题型一题型二题型三易错点:错用圆内接四边形的外角等于它的内角的对角这一定理而致错【例3】 如图,四边形ABCD是☉O的内接四边形,E为AB的延长线上一点,若∠CBE=40°,则∠AOC等于( )
A.20° B.40°
C.80° D.100°
错解:∵四边形ABCD是☉O的内接四边形,
∴根据圆内接四边形的外角等于它的内角的对角,得∠CBE=∠COA=40°.故选B.
错因分析:上述解答错误的原因是对性质定理2的理解不透彻,不能准确理解“外角等于它的内角的对角”的含义.所谓的“内角的对角”通常是指圆周角.题型一题型二题型三正解:∵四边形ABCD是圆内接四边形,且∠CBE=40°,由圆内接四边形的性质知∠D=∠CBE=40°.又由圆周角定理知∠AOC=2∠D=80°.
答案:C
