高中数学新人教A版选修4-1课件:2.4弦切角的性质(19张)
文档属性
| 名称 | 高中数学新人教A版选修4-1课件:2.4弦切角的性质(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 627.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 00:00:00 | ||
图片预览



文档简介
课件19张PPT。四 弦切角的性质1.理解弦切角的概念,会判断弦切角.
2.掌握弦切角定理的内容,并能利用定理解决有关问题.121.弦切角
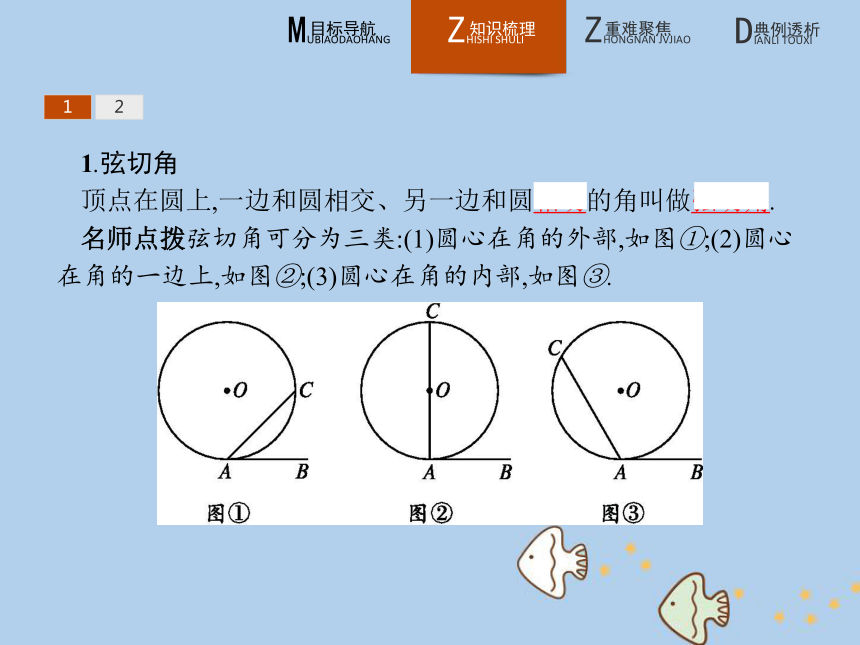
顶点在圆上,一边和圆相交、另一边和圆相切的角叫做弦切角.
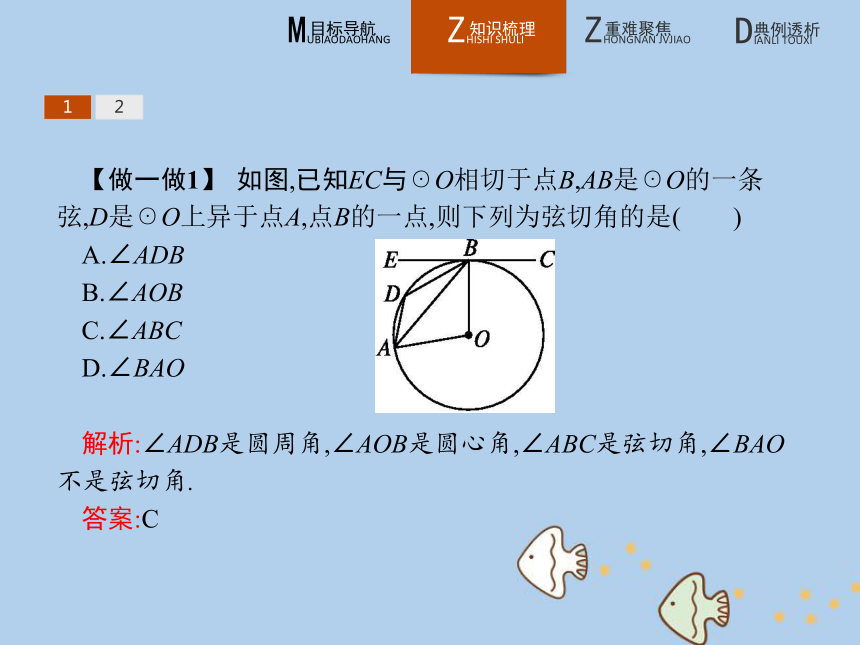
名师点拨弦切角可分为三类:(1)圆心在角的外部,如图①;(2)圆心在角的一边上,如图②;(3)圆心在角的内部,如图③.12【做一做1】 如图,已知EC与☉O相切于点B,AB是☉O的一条弦,D是☉O上异于点A,点B的一点,则下列为弦切角的是( )
A.∠ADB
B.∠AOB
C.∠ABC
D.∠BAO
解析:∠ADB是圆周角,∠AOB是圆心角,∠ABC是弦切角,∠BAO不是弦切角.
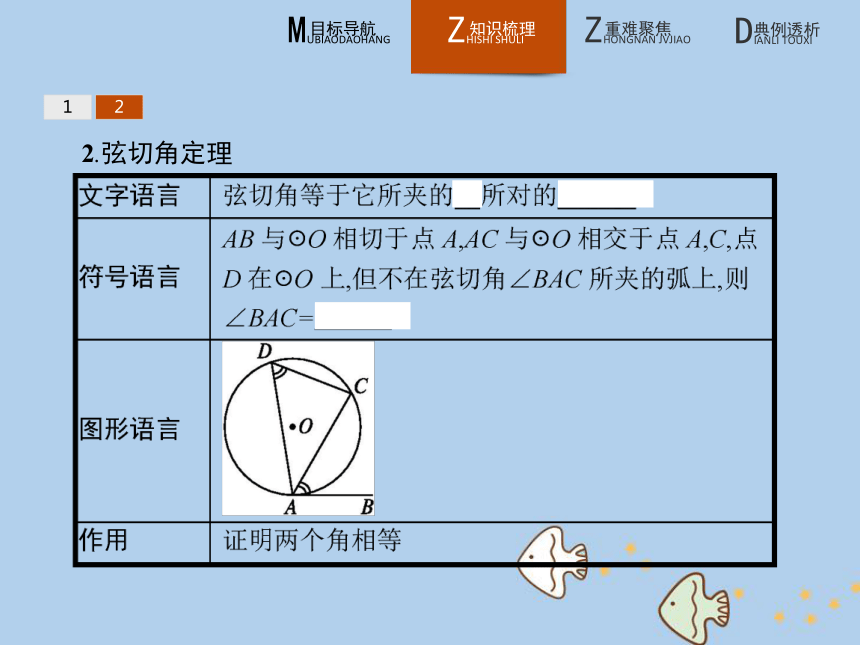
答案:C122.弦切角定理 12归纳总结1.弦切角定理的推论:若一个圆的两个弦切角所夹的弧相等,则这两个弦切角也相等.
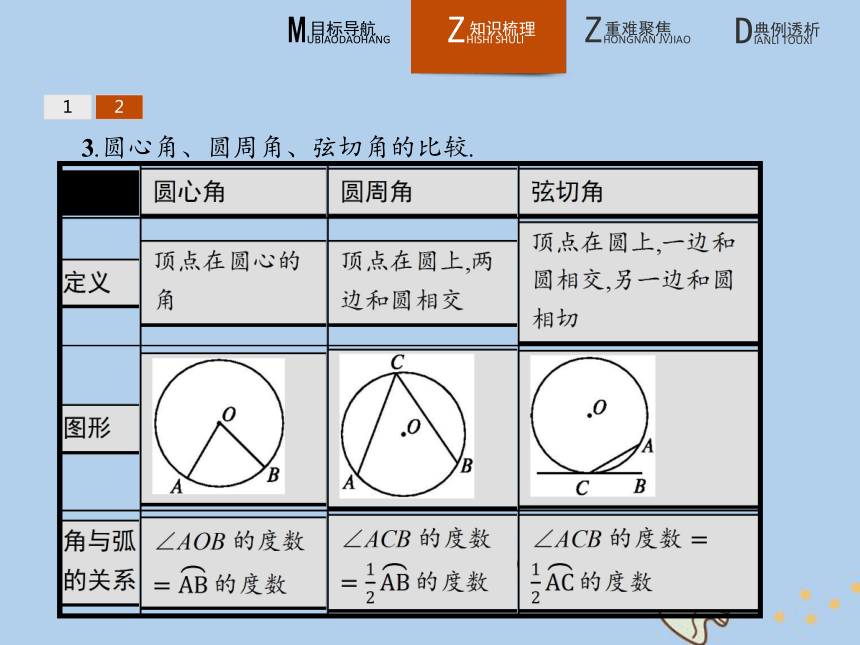
2.弦切角定理也可以表述为弦切角的度数等于它所夹的弧的度数的一半.这就建立了弦切角与弧之间的数量关系,它为直接依据弧进行角的转换确立了基础.123.圆心角、圆周角、弦切角的比较. 12【做一做2-1】 如图,MN与☉O相切于点M,Q和P是☉O上两点,若∠PQM=70°,则∠NMP等于( )
A.20°
B.70°
C.110°
D.160°
解析:∵∠NMP是弦切角,
∴∠NMP=∠PQM=70°.
答案:B12【做一做2-2】 过圆内接△ABC的顶点A引☉O的切线交BC的延长线于点D,若∠B=35°,∠ACB=80°,则∠D为 ( )
A.45° B.50° C.55° D.60°
解析:如图,∵AD为☉O的切线,
∴∠DAC=∠B=35°.
∵∠ACB=80°,
∴∠D=∠ACB-∠DAC=80°-35°=45°.
答案:A对弦切角的理解
剖析:弦切角的特点:(1)顶点在圆上;(2)一边与圆相交;(3)另一边与圆相切.
弦切角定义中的三个条件缺一不可.如图①②③④中的角都不是弦切角.图①中,缺少“顶点在圆上”的条件;图②中,缺少“一边和圆相交”的条件;图③中,缺少“一边和圆相切”的条件;图④中,缺少“顶点在圆上”和“另一边和圆相切”两个条件.题型一题型二题型三【例1】 如图,AD是△ABC中∠BAC的平分线,☉O经过点A且与BC切于点D,与AB,AC分别相交于点E,F.求证:EF∥BC.
分析:连接DF,于是∠FDC=∠DAC,根据AD是∠BAC的平分线,有∠BAD=∠DAC,而∠BAD与∠EFD对着同一段弧,由此得到∠EFD与∠FDC的相等关系,根据内错角相等,可以断定两条直线平行.题型一题型二题型三证明:如图,连接DF,
∵AD是∠BAC的平分线,
∴∠BAD=∠DAC.
∵∠EFD=∠BAD,
∴∠EFD=∠DAC.
∵BC切☉O于点D,
∴∠FDC=∠DAC.
∴∠EFD=∠FDC.∴EF∥BC.
反思当已知条件中出现圆的切线时,借助于弦切角定理,常用角的关系证明两条直线平行:①内错角相等,两条直线平行;②同位角相等,两条直线平行;③同旁内角互补,两条直线平行等.证明时可以根据图形与已知条件合理地选择.题型一题型二题型三【变式训练1】 如图,△ABC内接于☉O,AB的延长线与过点C的切线GC相交于点D,BE与AC相交于点F,且CB=CE.
求证:BE∥DG.
证明:∵CG为☉O的切线,
∴∠EBC=∠GCE.
∴∠EBC=∠E.∴∠E=∠GCE.
∴DG∥BE.题型一题型二题型三【例2】 已知△ABC内接于☉O,∠BAC的平分线交☉O于点D,CD的延长线交过点B的切线于点E.
分析:直接证明此等式有一定的难度,可以考虑把它分解成两个比例式的形式,借助相似三角形的性质得出结论.题型一题型二题型三证明:连接BD,如图.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
又∠BCD=∠BAD,
∠CBD=∠CAD,
∴∠BCD=∠CBD.
∴BD=CD.题型一题型二题型三又BE为☉O的切线,
∴∠EBD=∠BCD.
在△BED和△CEB中,
∠EBD=∠ECB,∠BED=∠CEB,
∴△BED∽△CEB.反思已知直线与圆相切,证明线段成比例时,常先利用弦切角定理和圆周角定理得到角相等,再通过三角形相似得到成比例线段.题型一题型二题型三【变式训练2】 如图,AB为☉O的直径,弦CD∥AB,AE切☉O于点A,交CD的延长线于点E.求证:BC2=AB·DE.
证明:如图,连接BD,OD,OC.
∵AE切☉O于点A,∴∠EAD=∠ABD,
且AE⊥AB.又AB∥CD,∴AE⊥CE,∴∠E=90°.
∵AB为☉O的直径,∴∠ADB=90°.
∴∠E=∠ADB,
∴△ADE∽△BAD,
∴AD2=AB·DE.
∵CD∥AB,∴∠1=∠2,∠3=∠4.
∵∠2=∠4,∴∠1=∠3,
∴AD=BC,∴BC2=AB·DE.题型一题型二题型三易错点:忽视弦切角的一边是切线致错
【例3】 如图,已知△ABC内接于☉O,AD⊥AC,∠C=32°,∠B=110°,则∠BAD= .?
错解:∵AD⊥AC,
∴∠BAD是弦切角.
∴∠BAD=∠C.
又∠C=32°,∴∠BAD=32°.
错因分析:错解中,误认为∠BAD是弦切角.虽然AD⊥AC,但AD不是切线.题型一题型二题型三正解:∵∠C+∠B+∠BAC=180°,
∴∠BAC=180°-∠C-∠B=38°.
又AD⊥AC,∴∠BAC+∠BAD=90°.
∴∠BAD=90°-∠BAC=90°-38°=52°.
答案:52°
反思在利用弦切角定理解决问题时,要注意所涉及的角是不是弦切角,即弦切角的三个条件缺一不可.
2.掌握弦切角定理的内容,并能利用定理解决有关问题.121.弦切角
顶点在圆上,一边和圆相交、另一边和圆相切的角叫做弦切角.
名师点拨弦切角可分为三类:(1)圆心在角的外部,如图①;(2)圆心在角的一边上,如图②;(3)圆心在角的内部,如图③.12【做一做1】 如图,已知EC与☉O相切于点B,AB是☉O的一条弦,D是☉O上异于点A,点B的一点,则下列为弦切角的是( )
A.∠ADB
B.∠AOB
C.∠ABC
D.∠BAO
解析:∠ADB是圆周角,∠AOB是圆心角,∠ABC是弦切角,∠BAO不是弦切角.
答案:C122.弦切角定理 12归纳总结1.弦切角定理的推论:若一个圆的两个弦切角所夹的弧相等,则这两个弦切角也相等.
2.弦切角定理也可以表述为弦切角的度数等于它所夹的弧的度数的一半.这就建立了弦切角与弧之间的数量关系,它为直接依据弧进行角的转换确立了基础.123.圆心角、圆周角、弦切角的比较. 12【做一做2-1】 如图,MN与☉O相切于点M,Q和P是☉O上两点,若∠PQM=70°,则∠NMP等于( )
A.20°
B.70°
C.110°
D.160°
解析:∵∠NMP是弦切角,
∴∠NMP=∠PQM=70°.
答案:B12【做一做2-2】 过圆内接△ABC的顶点A引☉O的切线交BC的延长线于点D,若∠B=35°,∠ACB=80°,则∠D为 ( )
A.45° B.50° C.55° D.60°
解析:如图,∵AD为☉O的切线,
∴∠DAC=∠B=35°.
∵∠ACB=80°,
∴∠D=∠ACB-∠DAC=80°-35°=45°.
答案:A对弦切角的理解
剖析:弦切角的特点:(1)顶点在圆上;(2)一边与圆相交;(3)另一边与圆相切.
弦切角定义中的三个条件缺一不可.如图①②③④中的角都不是弦切角.图①中,缺少“顶点在圆上”的条件;图②中,缺少“一边和圆相交”的条件;图③中,缺少“一边和圆相切”的条件;图④中,缺少“顶点在圆上”和“另一边和圆相切”两个条件.题型一题型二题型三【例1】 如图,AD是△ABC中∠BAC的平分线,☉O经过点A且与BC切于点D,与AB,AC分别相交于点E,F.求证:EF∥BC.
分析:连接DF,于是∠FDC=∠DAC,根据AD是∠BAC的平分线,有∠BAD=∠DAC,而∠BAD与∠EFD对着同一段弧,由此得到∠EFD与∠FDC的相等关系,根据内错角相等,可以断定两条直线平行.题型一题型二题型三证明:如图,连接DF,
∵AD是∠BAC的平分线,
∴∠BAD=∠DAC.
∵∠EFD=∠BAD,
∴∠EFD=∠DAC.
∵BC切☉O于点D,
∴∠FDC=∠DAC.
∴∠EFD=∠FDC.∴EF∥BC.
反思当已知条件中出现圆的切线时,借助于弦切角定理,常用角的关系证明两条直线平行:①内错角相等,两条直线平行;②同位角相等,两条直线平行;③同旁内角互补,两条直线平行等.证明时可以根据图形与已知条件合理地选择.题型一题型二题型三【变式训练1】 如图,△ABC内接于☉O,AB的延长线与过点C的切线GC相交于点D,BE与AC相交于点F,且CB=CE.
求证:BE∥DG.
证明:∵CG为☉O的切线,
∴∠EBC=∠GCE.
∴∠EBC=∠E.∴∠E=∠GCE.
∴DG∥BE.题型一题型二题型三【例2】 已知△ABC内接于☉O,∠BAC的平分线交☉O于点D,CD的延长线交过点B的切线于点E.
分析:直接证明此等式有一定的难度,可以考虑把它分解成两个比例式的形式,借助相似三角形的性质得出结论.题型一题型二题型三证明:连接BD,如图.
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD.
又∠BCD=∠BAD,
∠CBD=∠CAD,
∴∠BCD=∠CBD.
∴BD=CD.题型一题型二题型三又BE为☉O的切线,
∴∠EBD=∠BCD.
在△BED和△CEB中,
∠EBD=∠ECB,∠BED=∠CEB,
∴△BED∽△CEB.反思已知直线与圆相切,证明线段成比例时,常先利用弦切角定理和圆周角定理得到角相等,再通过三角形相似得到成比例线段.题型一题型二题型三【变式训练2】 如图,AB为☉O的直径,弦CD∥AB,AE切☉O于点A,交CD的延长线于点E.求证:BC2=AB·DE.
证明:如图,连接BD,OD,OC.
∵AE切☉O于点A,∴∠EAD=∠ABD,
且AE⊥AB.又AB∥CD,∴AE⊥CE,∴∠E=90°.
∵AB为☉O的直径,∴∠ADB=90°.
∴∠E=∠ADB,
∴△ADE∽△BAD,
∴AD2=AB·DE.
∵CD∥AB,∴∠1=∠2,∠3=∠4.
∵∠2=∠4,∴∠1=∠3,
∴AD=BC,∴BC2=AB·DE.题型一题型二题型三易错点:忽视弦切角的一边是切线致错
【例3】 如图,已知△ABC内接于☉O,AD⊥AC,∠C=32°,∠B=110°,则∠BAD= .?
错解:∵AD⊥AC,
∴∠BAD是弦切角.
∴∠BAD=∠C.
又∠C=32°,∴∠BAD=32°.
错因分析:错解中,误认为∠BAD是弦切角.虽然AD⊥AC,但AD不是切线.题型一题型二题型三正解:∵∠C+∠B+∠BAC=180°,
∴∠BAC=180°-∠C-∠B=38°.
又AD⊥AC,∴∠BAC+∠BAD=90°.
∴∠BAD=90°-∠BAC=90°-38°=52°.
答案:52°
反思在利用弦切角定理解决问题时,要注意所涉及的角是不是弦切角,即弦切角的三个条件缺一不可.
