高中数学新人教A版选修4-1课件:3.1平行射影(19张)
文档属性
| 名称 | 高中数学新人教A版选修4-1课件:3.1平行射影(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 229.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 09:45:32 | ||
图片预览






文档简介
课件19张PPT。第三讲 圆锥曲线性质的探讨一 平行射影1.掌握正射影的概念,理解平行射影的概念,能确定平行射影的形状.
2.掌握椭圆的定义,知道椭圆是圆柱的一种截面.1231.正射影
(1)定义:给定一个平面α,从一点A作平面α的垂线,垂足为点A'.称点A'为点A在平面α上的正射影.一个图形上各点在平面α上的正射影所组成的图形,称为这个图形在平面α上的正射影.
(2)圆面的正射影:一个圆所在的平面β与平面α平行,那么该圆在平面α上的正射影显然是一个圆,并且是和原来的圆相同的圆;如果圆所在的平面β与平面α不平行且不垂直时,从生活经验我们知道,正射影的形状发生了变化,就好像一个圆被压扁了,我们称之椭圆;如果圆所在的平面β与平面α垂直时,那么该圆在平面α上的正射影是一条线段,其长度等于圆的直径.123名师点拨一个图形在一个平面上的正射影与图形和平面的位置有关,如一条直线,当它和平面α垂直时,它在平面α上的正射影是一个点;当它和平面α斜交时,它在平面α上的正射影是一条直线;它和平面α平行时,它在平面α上的正射影是一条与原直线平行的直线.
【做一做1】 △ABC在平面α上的正射影是( )
A.三角形
B.直线
C.线段
D.三角形或线段
解析:当△ABC所在平面垂直于α时,△ABC在α上的正射影是一条线段,否则是三角形.
答案:D1232.平行射影
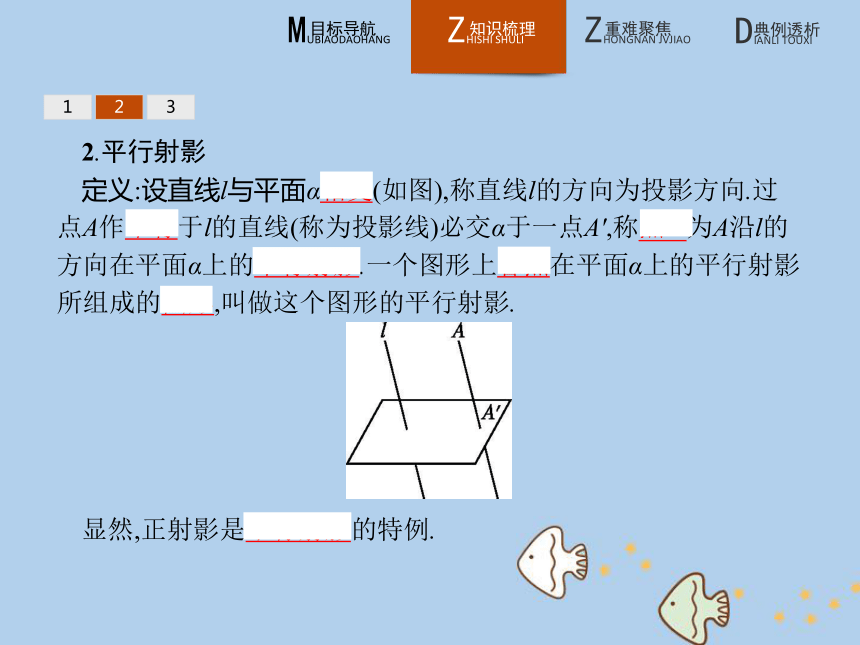
定义:设直线l与平面α相交(如图),称直线l的方向为投影方向.过点A作平行于l的直线(称为投影线)必交α于一点A',称点A'为A沿l的方向在平面α上的平行射影.一个图形上各点在平面α上的平行射影所组成的图形,叫做这个图形的平行射影.
显然,正射影是平行射影的特例.123归纳总结平行射影的性质:
(1)直线的平行射影是直线或一个点,线段的平行射影是线段或一个点;
(2)平行直线的平行射影是平行或重合的直线或两个点;
(3)平行于投影面的线段,它的平行射影与这条线段平行且等长;
(4)与投影面平行的平面图形,它的平行射影与这个图形全等;
(5)在同一直线或平行直线上的两条线段的平行射影(不是点)的比等于这两条线段的比.123【做一做2】 两条异面直线m和n在平面α上的平行射影是( )
A.一条直线和直线外一个点
B.两条相交直线
C.两条平行直线
D.以上都有可能
解析:当m和n中有一条直线与投影方向平行时,它们的平行射影是一个点和一条直线;否则是两条平行直线或相交直线.
答案:D1233.椭圆
(1)定义:平面上到两个定点的距离之和等于定长的点的轨迹叫做椭圆.
(2)抽象概括:用一个平面去截一个圆柱,当平面与圆柱的两个底面平行时,截面是一个圆;当平面与圆柱的两个底面不平行时,截面是一个椭圆(如图).123【做一做3】 平面上两个定点A和B的距离为5,动点P到点A,B的距离之和为常数m,若动点P的轨迹是椭圆,则m的取值范围是( )
A.(0,5) B.(5,+∞)
C.(0,+∞) D.R
解析:当m<5时,不表示任何图形;当m=5时,轨迹是线段AB;当m>5时,轨迹是椭圆.
答案:B1.平行射影与正射影的区别与联系
剖析:对于平行射影,取不同的投影方向,同一个图形的平行射影也有所不同,正射影就是平行射影中投影方向与平面垂直时的一种特殊情况.因而我们可以从两个不同的角度加以考虑,并且要注意这二者的区别与联系,从而完整、全面地看待问题.
例如,如图,直线l与平面α所成的角是45°,交点为A.在l上取不同于点A的一点B,过点B作BC⊥α,垂足为C.则l在平面α上的正射影是直线AC.当投影方向与l相同时,l在平面α上的平行射影是一个点,即点A;当投影方向垂直于平面α时,l在平面α上的平行射影是直线AC,此时平行射影和正射影是相同的.2.点的射影与图形的射影的区别与联系
剖析:图形是由点组成的集合,因而图形的射影是被投影图形上各点在平面α上的射影的集合,所以,要找到一个图形的射影只需找到组成这个图形的关键点的射影即可.题型一题型二题型三【例1】 下列说法正确的是( )
A.正射影和平行射影是两种截然不同的射影
B.投影线与投影平面有且只有一个交点
C.投影方向可以平行于投影平面
D.一个图形在某个平面上的平行射影是唯一的
解析:正射影是平行射影的特例,本质是相同的,故选项A错误;投影线与投影平面只能相交,选项B是正确的,选项C是错误的;一个图形在一个平面上的平行射影与投影方向有关,方向改变了,就可能得到不同的平行射影,故选项D错误.
答案:B
反思图形的平行射影与两个因素有关:一个是投影方向,一个是投影平面.正确理解平行射影的有关概念,是解决平行射影问题的关键.题型一题型二题型三【变式训练1】 若一个三角形的平行射影仍是一个三角形,则下列结论正确的是( )
A.内心的平行射影还是内心
B.重心的平行射影还是重心
C.垂心的平行射影还是垂心
D.外心的平行射影还是外心
解析:当三角形的平行射影仍是三角形时,其在投影平面上的三角形的形状可能会发生变化,此时三角形的各顶点、各边的位置也会发生变化,其中内心、垂心、外心这些由顶点和边确定的点会随着发生变化,而中线上三等分点的等分比例性质不变,重心射影前后相对的位置关系不变.
答案:B题型一题型二题型三【例2】 如图,已知点E,F分别为正方体的面ADD1A1,面BCC1B1的中心,则四边形BFD1E在该正方体的面上的正射影可能是 .(要求:把可能的图的序号都填上)?题型一题型二题型三解析:对四边形BFD1E在正方体的六个面上的正射影都要考虑到,并且对于图形要考虑所有点的正射影,又知线段由两个端点唯一确定,故考查四边形BFD1E的射影,只需同时考查点B,F,D1,E在各个面上的正射影即可.
四边形BFD1E在平面ABB1A1,平面CDD1C1,平面ABCD和平面A1B1C1D1上的正射影均为图②;四边形BFD1E在平面ADD1A1和平面BCC1B1上的正射影均为图③.
答案:②③
反思判断平行射影的形状时,常常先确定图形中各顶点的射影,再依次连接各顶点的射影即可;同一图形在平行平面上的平行射影是相同的.题型一题型二题型三【变式训练2】 如图,在正方体ABCD-A1B1C1D1中,E,F分别是AA1,D1C1的中点,G是正方形BCC1B1的中心,画出空间四边形AEFG在该正方体的面DCC1D1上的正投影.题型一题型二题型三解:如图①,点A落在D点上,点G 落在CC1的中点G'上,点F在面DCC1D1上的正射影仍为点F,点E落在DD1的中点E'上,所以其正投影如图②所示.题型一题型二题型三易错点:不能准确理解平行射影的概念而致错
【例3】 已知线段AB,CD在同一平面内的正射影相等,则线段AB,CD的长度关系为( )
A.AB>CD B.ABC.AB=CD D.无法确定
错解:因为线段AB,CD的正射影相等,所以线段AB,CD的长度也相等,故选C.
错因分析:上述错误的原因是不能正确理解正射影的定义,一个图形在一个平面上的正射影与图形和平面的位置有关.
正解:D
解析:由于线段AB,CD与平面所成的角未定,虽然正射影相等,但线段AB,CD的长度无法确定,故它们的长度关系也无法确定.故选D.
2.掌握椭圆的定义,知道椭圆是圆柱的一种截面.1231.正射影
(1)定义:给定一个平面α,从一点A作平面α的垂线,垂足为点A'.称点A'为点A在平面α上的正射影.一个图形上各点在平面α上的正射影所组成的图形,称为这个图形在平面α上的正射影.
(2)圆面的正射影:一个圆所在的平面β与平面α平行,那么该圆在平面α上的正射影显然是一个圆,并且是和原来的圆相同的圆;如果圆所在的平面β与平面α不平行且不垂直时,从生活经验我们知道,正射影的形状发生了变化,就好像一个圆被压扁了,我们称之椭圆;如果圆所在的平面β与平面α垂直时,那么该圆在平面α上的正射影是一条线段,其长度等于圆的直径.123名师点拨一个图形在一个平面上的正射影与图形和平面的位置有关,如一条直线,当它和平面α垂直时,它在平面α上的正射影是一个点;当它和平面α斜交时,它在平面α上的正射影是一条直线;它和平面α平行时,它在平面α上的正射影是一条与原直线平行的直线.
【做一做1】 △ABC在平面α上的正射影是( )
A.三角形
B.直线
C.线段
D.三角形或线段
解析:当△ABC所在平面垂直于α时,△ABC在α上的正射影是一条线段,否则是三角形.
答案:D1232.平行射影
定义:设直线l与平面α相交(如图),称直线l的方向为投影方向.过点A作平行于l的直线(称为投影线)必交α于一点A',称点A'为A沿l的方向在平面α上的平行射影.一个图形上各点在平面α上的平行射影所组成的图形,叫做这个图形的平行射影.
显然,正射影是平行射影的特例.123归纳总结平行射影的性质:
(1)直线的平行射影是直线或一个点,线段的平行射影是线段或一个点;
(2)平行直线的平行射影是平行或重合的直线或两个点;
(3)平行于投影面的线段,它的平行射影与这条线段平行且等长;
(4)与投影面平行的平面图形,它的平行射影与这个图形全等;
(5)在同一直线或平行直线上的两条线段的平行射影(不是点)的比等于这两条线段的比.123【做一做2】 两条异面直线m和n在平面α上的平行射影是( )
A.一条直线和直线外一个点
B.两条相交直线
C.两条平行直线
D.以上都有可能
解析:当m和n中有一条直线与投影方向平行时,它们的平行射影是一个点和一条直线;否则是两条平行直线或相交直线.
答案:D1233.椭圆
(1)定义:平面上到两个定点的距离之和等于定长的点的轨迹叫做椭圆.
(2)抽象概括:用一个平面去截一个圆柱,当平面与圆柱的两个底面平行时,截面是一个圆;当平面与圆柱的两个底面不平行时,截面是一个椭圆(如图).123【做一做3】 平面上两个定点A和B的距离为5,动点P到点A,B的距离之和为常数m,若动点P的轨迹是椭圆,则m的取值范围是( )
A.(0,5) B.(5,+∞)
C.(0,+∞) D.R
解析:当m<5时,不表示任何图形;当m=5时,轨迹是线段AB;当m>5时,轨迹是椭圆.
答案:B1.平行射影与正射影的区别与联系
剖析:对于平行射影,取不同的投影方向,同一个图形的平行射影也有所不同,正射影就是平行射影中投影方向与平面垂直时的一种特殊情况.因而我们可以从两个不同的角度加以考虑,并且要注意这二者的区别与联系,从而完整、全面地看待问题.
例如,如图,直线l与平面α所成的角是45°,交点为A.在l上取不同于点A的一点B,过点B作BC⊥α,垂足为C.则l在平面α上的正射影是直线AC.当投影方向与l相同时,l在平面α上的平行射影是一个点,即点A;当投影方向垂直于平面α时,l在平面α上的平行射影是直线AC,此时平行射影和正射影是相同的.2.点的射影与图形的射影的区别与联系
剖析:图形是由点组成的集合,因而图形的射影是被投影图形上各点在平面α上的射影的集合,所以,要找到一个图形的射影只需找到组成这个图形的关键点的射影即可.题型一题型二题型三【例1】 下列说法正确的是( )
A.正射影和平行射影是两种截然不同的射影
B.投影线与投影平面有且只有一个交点
C.投影方向可以平行于投影平面
D.一个图形在某个平面上的平行射影是唯一的
解析:正射影是平行射影的特例,本质是相同的,故选项A错误;投影线与投影平面只能相交,选项B是正确的,选项C是错误的;一个图形在一个平面上的平行射影与投影方向有关,方向改变了,就可能得到不同的平行射影,故选项D错误.
答案:B
反思图形的平行射影与两个因素有关:一个是投影方向,一个是投影平面.正确理解平行射影的有关概念,是解决平行射影问题的关键.题型一题型二题型三【变式训练1】 若一个三角形的平行射影仍是一个三角形,则下列结论正确的是( )
A.内心的平行射影还是内心
B.重心的平行射影还是重心
C.垂心的平行射影还是垂心
D.外心的平行射影还是外心
解析:当三角形的平行射影仍是三角形时,其在投影平面上的三角形的形状可能会发生变化,此时三角形的各顶点、各边的位置也会发生变化,其中内心、垂心、外心这些由顶点和边确定的点会随着发生变化,而中线上三等分点的等分比例性质不变,重心射影前后相对的位置关系不变.
答案:B题型一题型二题型三【例2】 如图,已知点E,F分别为正方体的面ADD1A1,面BCC1B1的中心,则四边形BFD1E在该正方体的面上的正射影可能是 .(要求:把可能的图的序号都填上)?题型一题型二题型三解析:对四边形BFD1E在正方体的六个面上的正射影都要考虑到,并且对于图形要考虑所有点的正射影,又知线段由两个端点唯一确定,故考查四边形BFD1E的射影,只需同时考查点B,F,D1,E在各个面上的正射影即可.
四边形BFD1E在平面ABB1A1,平面CDD1C1,平面ABCD和平面A1B1C1D1上的正射影均为图②;四边形BFD1E在平面ADD1A1和平面BCC1B1上的正射影均为图③.
答案:②③
反思判断平行射影的形状时,常常先确定图形中各顶点的射影,再依次连接各顶点的射影即可;同一图形在平行平面上的平行射影是相同的.题型一题型二题型三【变式训练2】 如图,在正方体ABCD-A1B1C1D1中,E,F分别是AA1,D1C1的中点,G是正方形BCC1B1的中心,画出空间四边形AEFG在该正方体的面DCC1D1上的正投影.题型一题型二题型三解:如图①,点A落在D点上,点G 落在CC1的中点G'上,点F在面DCC1D1上的正射影仍为点F,点E落在DD1的中点E'上,所以其正投影如图②所示.题型一题型二题型三易错点:不能准确理解平行射影的概念而致错
【例3】 已知线段AB,CD在同一平面内的正射影相等,则线段AB,CD的长度关系为( )
A.AB>CD B.AB
错解:因为线段AB,CD的正射影相等,所以线段AB,CD的长度也相等,故选C.
错因分析:上述错误的原因是不能正确理解正射影的定义,一个图形在一个平面上的正射影与图形和平面的位置有关.
正解:D
解析:由于线段AB,CD与平面所成的角未定,虽然正射影相等,但线段AB,CD的长度无法确定,故它们的长度关系也无法确定.故选D.
