高中数学新人教A版选修4-1课件:3.2平面与圆柱面的截线(19张)
文档属性
| 名称 | 高中数学新人教A版选修4-1课件:3.2平面与圆柱面的截线(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 616.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 09:43:33 | ||
图片预览




文档简介
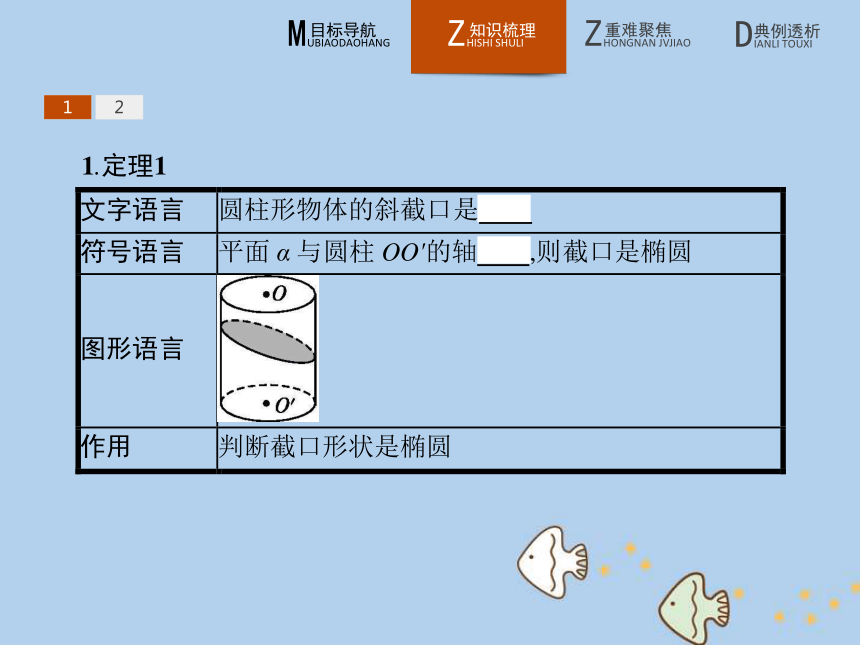
课件19张PPT。二 平面与圆柱面的截线1.通过圆柱形水杯中水面的倾斜,感受平面截圆柱的形式,并能证明定理1.
2.通过Dandelin双球探求椭圆的性质,体会这种证明问题的方法.121.定理1 12【做一做1】 圆柱形物体的截口是( )
A.双曲线 B.圆
C.抛物线 D.椭圆或圆
解析:当截面与圆柱的底面平行时,截口是圆,否则是椭圆.
答案:D122.椭圆
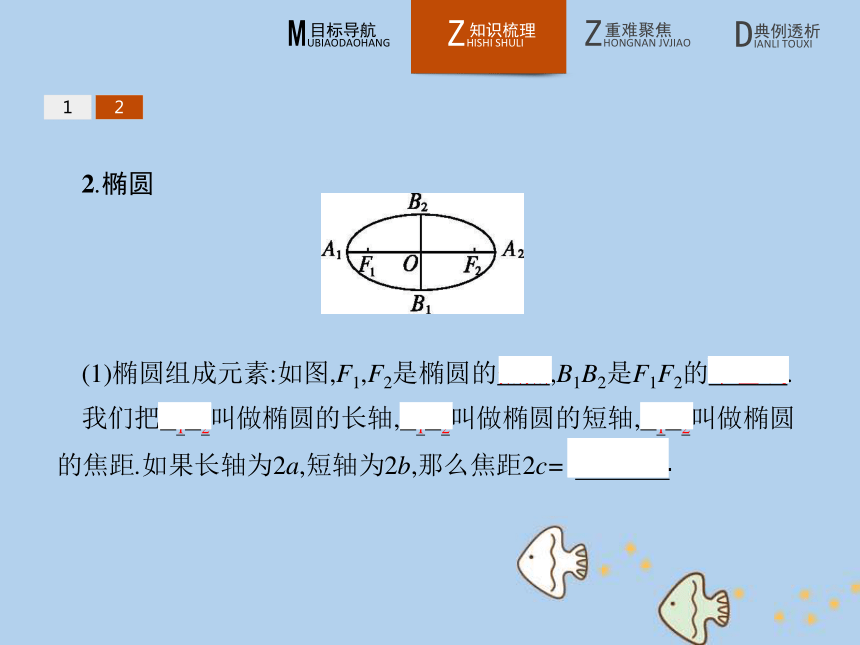
(1)椭圆组成元素:如图,F1,F2是椭圆的焦点,B1B2是F1F2的中垂线.
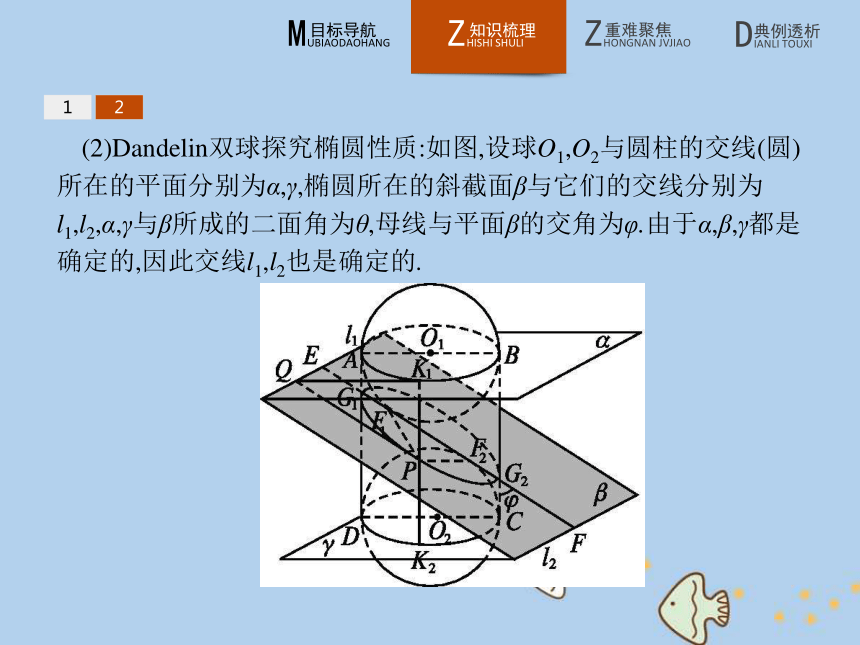
我们把A1A2叫做椭圆的长轴,B1B2叫做椭圆的短轴,F1F2叫做椭圆的焦距.如果长轴为2a,短轴为2b,那么焦距2c=12(2)Dandelin双球探究椭圆性质:如图,设球O1,O2与圆柱的交线(圆)所在的平面分别为α,γ,椭圆所在的斜截面β与它们的交线分别为l1,l2,α,γ与β所成的二面角为θ,母线与平面β的交角为φ.由于α,β,γ都是确定的,因此交线l1,l2也是确定的.12①当点P在椭圆的任意位置时,过点P作l1的垂线,垂足为点Q,过点P作平面α的垂线,垂足为点K1,连接K1Q,得Rt△PK1Q,则∠QPK1=φ.从而
②椭圆上任意一点到焦点F1的距离与到直线l1的距离之比为定值cos φ.我们把直线l1叫做椭圆的一条准线.?
③椭圆上任意一点到焦点F2的距离与到直线l2的距离之比也为定值cos φ,所以l2是椭圆的另一条准线.?
④记e=cos φ,我们把e叫做椭圆的离心率.12名师点拨e的几何意义是椭圆上一点到焦点的距离与它到准线的距离的比.当e越接近于1时,c越接近于a,从而b越小,因此椭圆越扁;反之,e越接近于0,从而b越接近于a,椭圆越接近于圆.当e=0时,c=0,a=b,两个焦点重合,图形就是圆了.可见离心率是刻画椭圆扁圆程度的量.12【做一做2-1】 已知F1和F2是椭圆的焦点,P是椭圆上的任一点,PF1=d1,PF2=d2,则( )
A.d1+d2是常数 B.d1-d2是常数
答案:A
解析:设椭圆的长轴长、短轴长、焦距分别为2a,2b,2c,则由题意,知2c=8,故c=4.
答案:1012【做一做2-3】 椭圆的长轴长为10,短轴长为8,则焦距等于( )
A.6 B.8
C.10 D.3
解析:设椭圆的长轴长、短轴长、焦距分别为2a,2b,2c,
则由题意,知2a=10,2b=8,
答案:ADandelin双球探求椭圆性质的过程
剖析:通过一条直线与相离的两个等圆的内公切线的情形,类比为两个半径相等的球在一个平面的两侧均与球相切的情形,从而得到定理1及有关结论,因而对于平面内直线与两个相离的等圆的内公切的情形要注意研究,这有助于理解椭圆和下一节的知识.
圆柱内嵌入两个球,使它们分别位于斜截面的上方和下方,并且与圆柱和斜截面均相切,这是证明定理的关键.这种方法是数学家Dandelin创立的,故将嵌入的两球称为Dandelin双球.要注意对于Dandelin双球的研究.题型一题型二题型三【例1】 已知平面α与一圆柱的母线成60°角,则该平面与圆柱截口图形的离心率是( )
答案:D
反思圆柱形物体的斜截口是椭圆,因此,椭圆的度量性质和底面半径、截面与母线的夹角密切相关.题型一题型二题型三【变式训练1】 底面直径为12 cm的圆柱被与底面成30°的平面所截,截口是一个椭圆,该椭圆的长轴长 ,短轴长 ?,离心率为 ?.?题型一题型二题型三【例2】 如图,已知球O1,O2分别切平面β于点F1,F2,P1P2为☉O1的一条直径,点Q1,Q2分别为点P1,P2在平面β内的平行射影,G1G2=2a,Q1Q2=2b,G1G2与Q1Q2互相垂直平分.题型一题型二题型三证明:如图,过点G1作G1H⊥BG2,H为垂足,
则四边形ABHG1是矩形.∴G1H=AB.
∵点Q1,Q2分别是点P1,P2的平行射影,∴P1Q1??P2Q2.
∴四边形P1Q1Q2P2是平行四边形.
∴Q1Q2=P1P2,即Q1Q2等于底面直径.
∴G1H=AB=Q1Q2=2b.
又由切线长定理,知G1A=G1F1=G2F2,G2F1=G2B,
∴G2F1-G2F2=G2B-G1A.
又G1A=BH,∴G2F1-G2F2=G2B-BH.∴F1F2=G2H.题型一题型二题型三反思探究圆柱体的斜截口——椭圆的性质时,需考察Dandelin双球与圆柱及其截面的关系,综合应用切线长定理、三角形的相似与全等、解直角三角形及平行射影的性质.题型一题型二题型三【变式训练2】 设平面π与圆柱的轴的夹角为β(0°<β<90°),现放入Dandelin双球使之与圆柱面和平面π都相切,若已知Dandelin双球与平面π的两切点的距离恰好等于圆柱的底面直径,则截线椭圆的离心率为( )解析:Dandelin双球与平面π的切点恰好是椭圆的焦点,圆柱的底面直径恰好等于椭圆的短轴长,由题意知,2b=2c.
答案:B题型一题型二题型三易错点:概念不清而致错
【例3】 如图,一个底面半径为R的圆柱被与其底面所成角为θ(0°<θ<90°)的平面所截,截面是一个椭圆.当θ=30°时,这个椭圆的离心率为( )
错解:由题易知,平面与圆柱的截口为椭圆,所以离心率
错因分析:上述解法错在没有正确理解椭圆的离心率的求解方法,在利用公式e=cos φ时,φ必须是圆柱的母线与平面的夹角.题型一题型二题型三正解:A
2.通过Dandelin双球探求椭圆的性质,体会这种证明问题的方法.121.定理1 12【做一做1】 圆柱形物体的截口是( )
A.双曲线 B.圆
C.抛物线 D.椭圆或圆
解析:当截面与圆柱的底面平行时,截口是圆,否则是椭圆.
答案:D122.椭圆
(1)椭圆组成元素:如图,F1,F2是椭圆的焦点,B1B2是F1F2的中垂线.
我们把A1A2叫做椭圆的长轴,B1B2叫做椭圆的短轴,F1F2叫做椭圆的焦距.如果长轴为2a,短轴为2b,那么焦距2c=12(2)Dandelin双球探究椭圆性质:如图,设球O1,O2与圆柱的交线(圆)所在的平面分别为α,γ,椭圆所在的斜截面β与它们的交线分别为l1,l2,α,γ与β所成的二面角为θ,母线与平面β的交角为φ.由于α,β,γ都是确定的,因此交线l1,l2也是确定的.12①当点P在椭圆的任意位置时,过点P作l1的垂线,垂足为点Q,过点P作平面α的垂线,垂足为点K1,连接K1Q,得Rt△PK1Q,则∠QPK1=φ.从而
②椭圆上任意一点到焦点F1的距离与到直线l1的距离之比为定值cos φ.我们把直线l1叫做椭圆的一条准线.?
③椭圆上任意一点到焦点F2的距离与到直线l2的距离之比也为定值cos φ,所以l2是椭圆的另一条准线.?
④记e=cos φ,我们把e叫做椭圆的离心率.12名师点拨e的几何意义是椭圆上一点到焦点的距离与它到准线的距离的比.当e越接近于1时,c越接近于a,从而b越小,因此椭圆越扁;反之,e越接近于0,从而b越接近于a,椭圆越接近于圆.当e=0时,c=0,a=b,两个焦点重合,图形就是圆了.可见离心率是刻画椭圆扁圆程度的量.12【做一做2-1】 已知F1和F2是椭圆的焦点,P是椭圆上的任一点,PF1=d1,PF2=d2,则( )
A.d1+d2是常数 B.d1-d2是常数
答案:A
解析:设椭圆的长轴长、短轴长、焦距分别为2a,2b,2c,则由题意,知2c=8,故c=4.
答案:1012【做一做2-3】 椭圆的长轴长为10,短轴长为8,则焦距等于( )
A.6 B.8
C.10 D.3
解析:设椭圆的长轴长、短轴长、焦距分别为2a,2b,2c,
则由题意,知2a=10,2b=8,
答案:ADandelin双球探求椭圆性质的过程
剖析:通过一条直线与相离的两个等圆的内公切线的情形,类比为两个半径相等的球在一个平面的两侧均与球相切的情形,从而得到定理1及有关结论,因而对于平面内直线与两个相离的等圆的内公切的情形要注意研究,这有助于理解椭圆和下一节的知识.
圆柱内嵌入两个球,使它们分别位于斜截面的上方和下方,并且与圆柱和斜截面均相切,这是证明定理的关键.这种方法是数学家Dandelin创立的,故将嵌入的两球称为Dandelin双球.要注意对于Dandelin双球的研究.题型一题型二题型三【例1】 已知平面α与一圆柱的母线成60°角,则该平面与圆柱截口图形的离心率是( )
答案:D
反思圆柱形物体的斜截口是椭圆,因此,椭圆的度量性质和底面半径、截面与母线的夹角密切相关.题型一题型二题型三【变式训练1】 底面直径为12 cm的圆柱被与底面成30°的平面所截,截口是一个椭圆,该椭圆的长轴长 ,短轴长 ?,离心率为 ?.?题型一题型二题型三【例2】 如图,已知球O1,O2分别切平面β于点F1,F2,P1P2为☉O1的一条直径,点Q1,Q2分别为点P1,P2在平面β内的平行射影,G1G2=2a,Q1Q2=2b,G1G2与Q1Q2互相垂直平分.题型一题型二题型三证明:如图,过点G1作G1H⊥BG2,H为垂足,
则四边形ABHG1是矩形.∴G1H=AB.
∵点Q1,Q2分别是点P1,P2的平行射影,∴P1Q1??P2Q2.
∴四边形P1Q1Q2P2是平行四边形.
∴Q1Q2=P1P2,即Q1Q2等于底面直径.
∴G1H=AB=Q1Q2=2b.
又由切线长定理,知G1A=G1F1=G2F2,G2F1=G2B,
∴G2F1-G2F2=G2B-G1A.
又G1A=BH,∴G2F1-G2F2=G2B-BH.∴F1F2=G2H.题型一题型二题型三反思探究圆柱体的斜截口——椭圆的性质时,需考察Dandelin双球与圆柱及其截面的关系,综合应用切线长定理、三角形的相似与全等、解直角三角形及平行射影的性质.题型一题型二题型三【变式训练2】 设平面π与圆柱的轴的夹角为β(0°<β<90°),现放入Dandelin双球使之与圆柱面和平面π都相切,若已知Dandelin双球与平面π的两切点的距离恰好等于圆柱的底面直径,则截线椭圆的离心率为( )解析:Dandelin双球与平面π的切点恰好是椭圆的焦点,圆柱的底面直径恰好等于椭圆的短轴长,由题意知,2b=2c.
答案:B题型一题型二题型三易错点:概念不清而致错
【例3】 如图,一个底面半径为R的圆柱被与其底面所成角为θ(0°<θ<90°)的平面所截,截面是一个椭圆.当θ=30°时,这个椭圆的离心率为( )
错解:由题易知,平面与圆柱的截口为椭圆,所以离心率
错因分析:上述解法错在没有正确理解椭圆的离心率的求解方法,在利用公式e=cos φ时,φ必须是圆柱的母线与平面的夹角.题型一题型二题型三正解:A
