高中数学新人教A版选修4-1课件:3.3平面与圆锥面的截线(19张)
文档属性
| 名称 | 高中数学新人教A版选修4-1课件:3.3平面与圆锥面的截线(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 733.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 09:44:17 | ||
图片预览



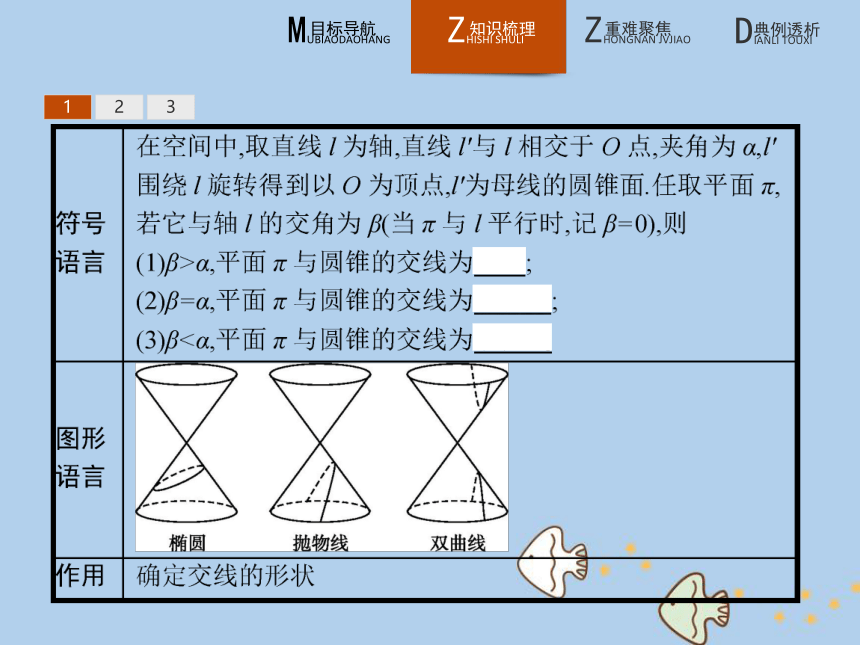



文档简介
课件19张PPT。三 平面与圆锥面的截线1.了解不平行于底面且不通过圆锥的顶点的平面截圆锥的形状是椭圆、抛物线、双曲线.
2.感受平面截圆锥的形状,并从理论上证明.
3.通过Dandelin双球探求双曲线的性质,理解这种证明问题的方法.1231.定理2 123123名师点拨
2.圆锥曲线的统一性,椭圆为封闭图形,双曲线、抛物线为不封闭图形,其图形不一样,但它们都可以用平面截对顶圆锥面得到,因此,圆、椭圆、双曲线、抛物线统称为圆锥曲线.它们都满足曲线上的点到焦点的距离与到准线的距离之比为常数,即离心率e.1232.圆锥曲线的结构特点
(1)椭圆上的点到两个定点(焦点)的距离之和为常数(长轴长2a).
(2)双曲线上的点到两个定点(焦点)的距离之差的绝对值为常数(2a).
(3)抛物线上的点到一个定点(焦点)和一条定直线的距离相等.
【做一做1】 双曲线上任意一点到两个焦点的距离分别是d1和d2,则下列为常数的是( )
A.d1-d2 B.d1+d2
C.|d1-d2| D.d2-d1
答案:C1233.圆锥曲线的几何性质
(1)焦点:Dandelin球与平面π的切点.
(2)准线:截面与Dandelin球和圆锥交线所在平面的交线.123(4)圆锥曲线的几何性质 123【做一做2-1】 设截面和圆锥的轴的夹角为β,圆锥的母线和轴所成角为α,当截面是椭圆时,其离心率等于( )
答案:B
【做一做2-2】 双曲线的焦距为4,实轴长为3,则离心率e= .?
解析:设双曲线的实轴长、虚轴长、焦距分别为2a,2b,2c,则2c=4,2a=3,在定理2中,当β<α时,探究截线形状
剖析:如图,当β<α时,平面π与圆锥面的两部分相交,在圆锥的两部分分别嵌入Dandelin球,与平面π的两个切点分别为F1,F2,与圆锥两部分截的圆分别为S1,S2.在截口上任取一点P,连接PF1,PF2.过点P和圆锥的顶点O作母线,分别与两球切于Q1,Q2点,则PF1=PQ1,PF2=PQ2,所以|PF1-PF2|=|PQ1-PQ2|=Q1Q2,所以Q1Q2是两圆S1,S2所在平行平面间的母线段的长,且为定值.
所以由双曲线的定义知,点P的轨迹为双曲线.题型一题型二题型三【例1】 如图,讨论其中双曲线的离心率.其中π'是Dandelin球与圆锥交线S2所在的平面,与π的交线为m.
题型一题型二题型三∵PB平行于圆锥的轴,∴∠BPA=β,∠BPQ2=α.
反思讨论圆锥曲线的几何性质时,要注意结合图形进行.解:点P是双曲线上任意一点,连接PF2,过点P作PA⊥m于点A,过点P作PB⊥平面π'于点B,连接AB,过点P作母线交S2于点Q2,连接BQ2.题型一题型二题型三【变式训练1】 在圆锥内部嵌入Dandelin双球,一个位于平面π的上方,一个位于平面π的下方,并且与平面π及圆锥均相切.若平面π与双球的切点不重合,则平面π与圆锥面的截线是( )
A.圆 B.椭圆 C.双曲线 D.抛物线
解析:由于平面π与双球的切点不重合,则平面π与圆锥母线不平行,且只与圆锥的一半相交,则截线是椭圆.
答案:B题型一题型二题型三【例2】 已知双曲线两个顶点间的距离为2a,焦距为2c,求两条准线间的距离.
解:如图,l1,l2是双曲线的准线,F1,F2是焦点,A1,A2是顶点,O为中心.题型一题型二题型三题型一题型二题型三【变式训练2】 顶角为60°的圆锥面中有一个半径为2的内切球,以该球为焦球作一截面,使截线为抛物线,求该抛物线的顶点到焦点的距题型一题型二题型三解:如图是圆锥的截面,其中点P为抛物线的顶点,点Q为抛物线的焦点,点M为截面与轴的交点,连接OA,OQ.
设A,B为球与圆锥的母线的切点.
由∠ASB=60°,
∴∠ASO=30°.
又OA=2,OA⊥SA,∴OS=4,易知OP⊥OS,
又PM∥SB,∴∠PMS=∠OSB=∠OSA,
∴SM=2OS=8.题型一题型二题型三易错点:错用圆锥曲线的离心率公式而致错
【例3】 已知圆锥面的轴截面为等腰直角三角形,用一个与轴线成30°角的不过圆锥顶点的平面去截圆锥面时,所截得的截线的离心率为( )错解:因为圆锥面的截面为等腰直角三角形,所以母线与轴线的夹角为45°.
又因为截面与轴线的夹角为30°,所以截线的离心率为题型一题型二题型三正解:A
解析:∵圆锥的轴截面为等腰直角三角形,所以母线与轴线的夹角α=45°.
又截面与轴线的夹角β=30°,即β<α,∴截线是双曲线,其离心率
2.感受平面截圆锥的形状,并从理论上证明.
3.通过Dandelin双球探求双曲线的性质,理解这种证明问题的方法.1231.定理2 123123名师点拨
2.圆锥曲线的统一性,椭圆为封闭图形,双曲线、抛物线为不封闭图形,其图形不一样,但它们都可以用平面截对顶圆锥面得到,因此,圆、椭圆、双曲线、抛物线统称为圆锥曲线.它们都满足曲线上的点到焦点的距离与到准线的距离之比为常数,即离心率e.1232.圆锥曲线的结构特点
(1)椭圆上的点到两个定点(焦点)的距离之和为常数(长轴长2a).
(2)双曲线上的点到两个定点(焦点)的距离之差的绝对值为常数(2a).
(3)抛物线上的点到一个定点(焦点)和一条定直线的距离相等.
【做一做1】 双曲线上任意一点到两个焦点的距离分别是d1和d2,则下列为常数的是( )
A.d1-d2 B.d1+d2
C.|d1-d2| D.d2-d1
答案:C1233.圆锥曲线的几何性质
(1)焦点:Dandelin球与平面π的切点.
(2)准线:截面与Dandelin球和圆锥交线所在平面的交线.123(4)圆锥曲线的几何性质 123【做一做2-1】 设截面和圆锥的轴的夹角为β,圆锥的母线和轴所成角为α,当截面是椭圆时,其离心率等于( )
答案:B
【做一做2-2】 双曲线的焦距为4,实轴长为3,则离心率e= .?
解析:设双曲线的实轴长、虚轴长、焦距分别为2a,2b,2c,则2c=4,2a=3,在定理2中,当β<α时,探究截线形状
剖析:如图,当β<α时,平面π与圆锥面的两部分相交,在圆锥的两部分分别嵌入Dandelin球,与平面π的两个切点分别为F1,F2,与圆锥两部分截的圆分别为S1,S2.在截口上任取一点P,连接PF1,PF2.过点P和圆锥的顶点O作母线,分别与两球切于Q1,Q2点,则PF1=PQ1,PF2=PQ2,所以|PF1-PF2|=|PQ1-PQ2|=Q1Q2,所以Q1Q2是两圆S1,S2所在平行平面间的母线段的长,且为定值.
所以由双曲线的定义知,点P的轨迹为双曲线.题型一题型二题型三【例1】 如图,讨论其中双曲线的离心率.其中π'是Dandelin球与圆锥交线S2所在的平面,与π的交线为m.
题型一题型二题型三∵PB平行于圆锥的轴,∴∠BPA=β,∠BPQ2=α.
反思讨论圆锥曲线的几何性质时,要注意结合图形进行.解:点P是双曲线上任意一点,连接PF2,过点P作PA⊥m于点A,过点P作PB⊥平面π'于点B,连接AB,过点P作母线交S2于点Q2,连接BQ2.题型一题型二题型三【变式训练1】 在圆锥内部嵌入Dandelin双球,一个位于平面π的上方,一个位于平面π的下方,并且与平面π及圆锥均相切.若平面π与双球的切点不重合,则平面π与圆锥面的截线是( )
A.圆 B.椭圆 C.双曲线 D.抛物线
解析:由于平面π与双球的切点不重合,则平面π与圆锥母线不平行,且只与圆锥的一半相交,则截线是椭圆.
答案:B题型一题型二题型三【例2】 已知双曲线两个顶点间的距离为2a,焦距为2c,求两条准线间的距离.
解:如图,l1,l2是双曲线的准线,F1,F2是焦点,A1,A2是顶点,O为中心.题型一题型二题型三题型一题型二题型三【变式训练2】 顶角为60°的圆锥面中有一个半径为2的内切球,以该球为焦球作一截面,使截线为抛物线,求该抛物线的顶点到焦点的距题型一题型二题型三解:如图是圆锥的截面,其中点P为抛物线的顶点,点Q为抛物线的焦点,点M为截面与轴的交点,连接OA,OQ.
设A,B为球与圆锥的母线的切点.
由∠ASB=60°,
∴∠ASO=30°.
又OA=2,OA⊥SA,∴OS=4,易知OP⊥OS,
又PM∥SB,∴∠PMS=∠OSB=∠OSA,
∴SM=2OS=8.题型一题型二题型三易错点:错用圆锥曲线的离心率公式而致错
【例3】 已知圆锥面的轴截面为等腰直角三角形,用一个与轴线成30°角的不过圆锥顶点的平面去截圆锥面时,所截得的截线的离心率为( )错解:因为圆锥面的截面为等腰直角三角形,所以母线与轴线的夹角为45°.
又因为截面与轴线的夹角为30°,所以截线的离心率为题型一题型二题型三正解:A
解析:∵圆锥的轴截面为等腰直角三角形,所以母线与轴线的夹角α=45°.
又截面与轴线的夹角β=30°,即β<α,∴截线是双曲线,其离心率
