高中数学新人教A版选修4-1课件:第二讲 直线与圆的位置关系本讲整合(25张)
文档属性
| 名称 | 高中数学新人教A版选修4-1课件:第二讲 直线与圆的位置关系本讲整合(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 767.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 09:45:15 | ||
图片预览




文档简介
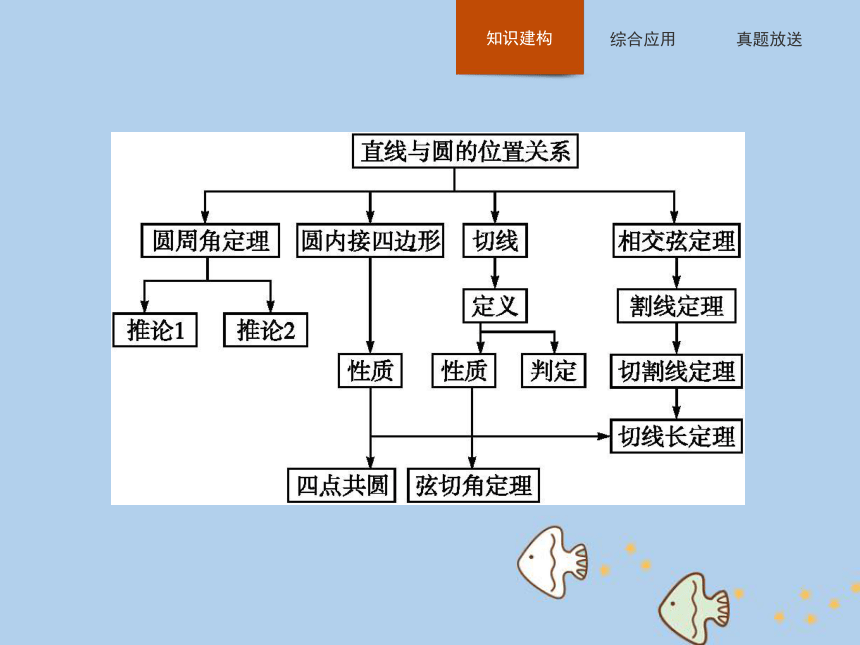
课件25张PPT。本讲整合专题一专题二专题一 与圆有关的角的计算与证明
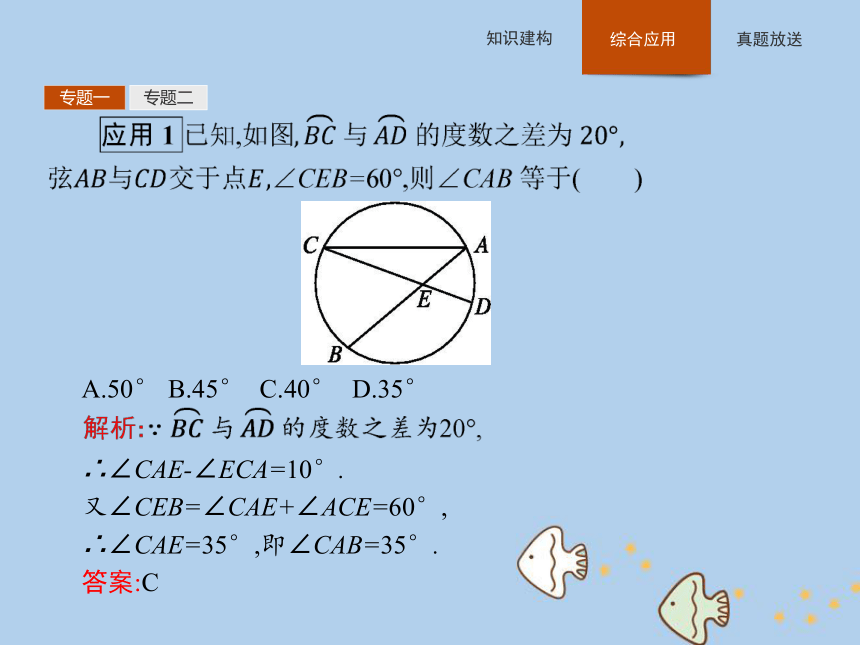
圆中的角有四类:圆心角、圆周角、弦切角和弧所对的角,与圆有关的角的计算与证明通常涉及这四类角,因此圆周角定理、圆心角定理和弦切角定理是解决此类问题的知识基础,通常利用圆周角、弦切角、圆心角与弧的关系来转化,并借助于圆内接四边形的对角互补和圆的切线垂直于经过切点的半径来解决.专题一专题二A.50° B.45° C.40° D.35° ∴∠CAE-∠ECA=10°.
又∠CEB=∠CAE+∠ACE=60°,
∴∠CAE=35°,即∠CAB=35°.
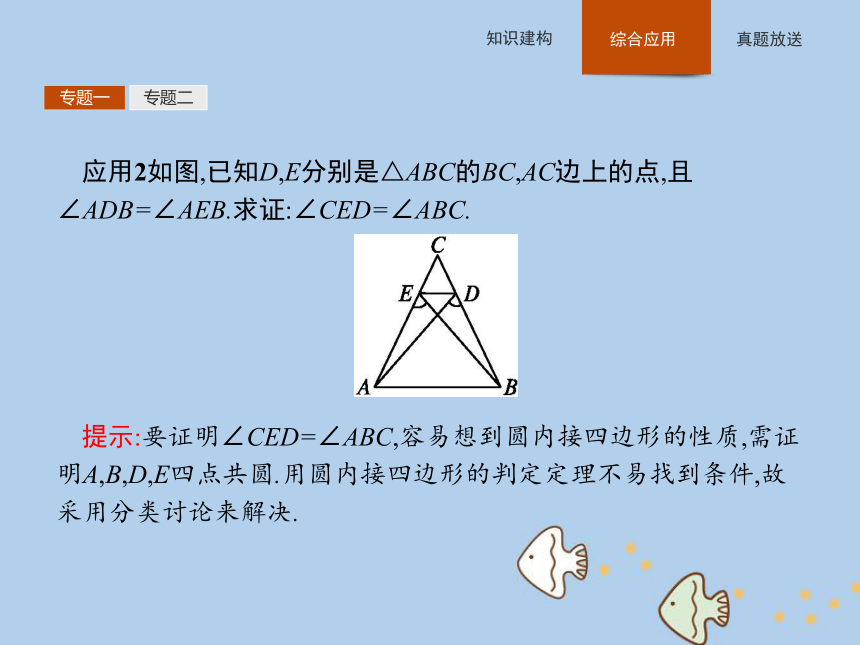
答案:C专题一专题二应用2如图,已知D,E分别是△ABC的BC,AC边上的点,且∠ADB=∠AEB.求证:∠CED=∠ABC.
提示:要证明∠CED=∠ABC,容易想到圆内接四边形的性质,需证明A,B,D,E四点共圆.用圆内接四边形的判定定理不易找到条件,故采用分类讨论来解决.专题一专题二证明:作△ABE的外接圆,则点D与外接圆有三种位置关系:①点D在圆外;②点D在圆内;③点D在圆上.
(1)如果点D在圆外,设BD与圆交于点F,连接AF,
如图.则∠AFB=∠AEB.而∠AEB=∠ADB,则
∠AFB=∠ADB.这与“三角形的外角大于任一
不相邻的内角”矛盾.故点D不能在圆外.
(2)如果点D在圆内,设圆与BD的延长线交于点F,连接AF,如图,
则∠AFB=∠AEB.
又因为∠AEB=∠ADB,
所以∠AFB=∠ADB.
这也与“三角形的外角大于任一不相邻的内角”矛盾.
故点D不可能在圆内.综上可得,点A,B,D,E在同一圆上.所以∠CED=∠ABC.专题一专题二专题二 与圆有关的线段的计算与证明
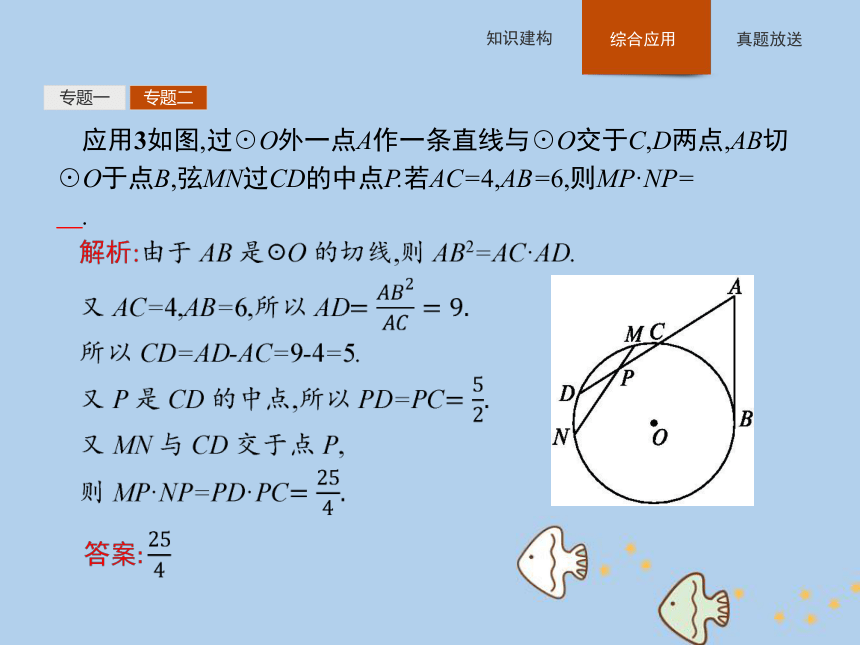
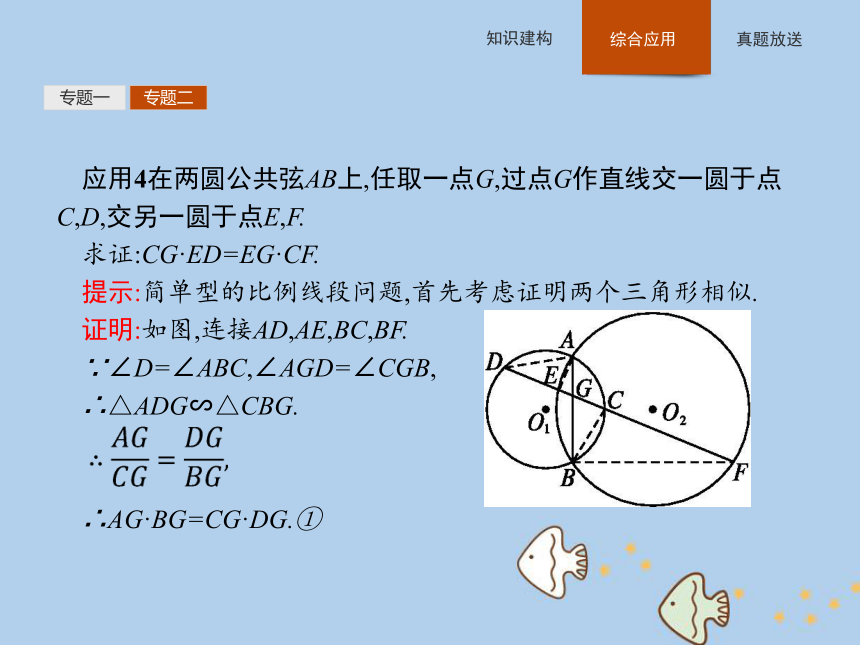
在圆中,解决与圆有关的线段的计算与证明问题时,先考虑圆幂定理,即相交弦定理、割线定理、切割线定理和切线长定理,得到成比例线段,再结合射影定理、相似三角形进行等比代换或等量代换加以证明或列出方程解得线段的长.专题一专题二应用3如图,过☉O外一点A作一条直线与☉O交于C,D两点,AB切☉O于点B,弦MN过CD的中点P.若AC=4,AB=6,则MP·NP= .?专题一专题二应用4在两圆公共弦AB上,任取一点G,过点G作直线交一圆于点C,D,交另一圆于点E,F.
求证:CG·ED=EG·CF.
提示:简单型的比例线段问题,首先考虑证明两个三角形相似.
证明:如图,连接AD,AE,BC,BF.
∵∠D=∠ABC,∠AGD=∠CGB,
∴△ADG∽△CBG.
∴AG·BG=CG·DG.①专题一专题二234156781(天津高考)如图,在圆O中,M,N是弦AB的三等分点,弦CD,CE分别经过点M,N.若CM=2,MD=4,CN=3,则线段NE的长为( )23415678解析:由相交弦定理,
因为M,N是弦AB的三等分点,
所以AM=MN=NB,MB=AN.
所以AM·MB=AN·NB.
答案:A23415678解析:由切割线定理得EC2=EB·EA,
即12=EB·(EB+4),可求得EB=2.
连接OC,则OC⊥DE,所以OC∥AD,答案:3 2(广东高考)如图,AB为圆O的直径,E为AB延长线上一点,过E作圆O的切线,切点为C,过A作直线EC的垂线,垂足为D.若AB=4,CE=234156783(重庆高考)如图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,PC=3,CE∶ED=2∶1,则BE= .?
解析:因为PA是圆的切线,
所以有PA2=PC·PD,
因此CD=PD-PC=9.
又因为CE∶ED=2∶1,所以CE=6,ED=3.
又由相交弦定理可得AE·BE=CE·ED,
答案:2234156784(广东高考)如图,已知AB是圆O的直径,AB=4,EC是圆O的切线,切点为C,BC=1,过圆心O作BC的平行线,分别交EC和AC于点D和点P,则OD= .?23415678答案:8 234156785(课标全国Ⅰ高考)如图,AB是☉O的直径,AC是☉O的切线,BC交☉O于点E.
(1)若D为AC的中点,证明:DE是☉O的切线;23415678解:(1)连接AE,由已知得,AE⊥BC,AC⊥AB.
在Rt△AEC中,由已知得,DE=DC,故∠DEC=∠DCE.
连接OE,则∠OBE=∠OEB.
又∠ACB+∠ABC=90°,
所以∠DEC+∠OEB=90°,
故∠OED=90°,DE是☉O的切线.234156786(课标全国Ⅱ高考)如图,O为等腰三角形ABC内一点,☉O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.
(1)证明:EF∥BC;
(2)若AG等于☉O的半径,且AE=MN=23415678解:(1)由于△ABC是等腰三角形,AD⊥BC,所以AD是∠CAB的平分线.
又因为☉O分别与AB,AC相切于点E,F,
所以AE=AF,故AD⊥EF.
从而EF∥BC.
(2)由(1)知,AE=AF,AD⊥EF,
故AD是EF的垂直平分线.
又EF为☉O的弦,所以O在AD上.
连接OE,OM,则OE⊥AE.23415678由AG等于☉O的半径得AO=2OE,
所以∠OAE=30°.
因此△ABC和△AEF都是等边三角形.234156787(课标全国Ⅰ高考)如图,四边形ABCD是☉O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
(1)证明:∠D=∠E;
(2)设AD不是☉O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.23415678(1)证明:由题设知A,B,C,D四点共圆,所以∠D=∠CBE.
由已知得∠CBE=∠E,故∠D=∠E.
(2)解:设BC的中点为N,连接MN,则由MB=MC,知MN⊥BC,故O在直线MN上.
又AD不是☉O的直径,M为AD的中点,
故OM⊥AD,即MN⊥AD.
所以AD∥BC,故∠A=∠CBE.
又∠CBE=∠E,故∠A=∠E.
由(1)知,∠D=∠E,所以△ADE为等边三角形.234156788(课标全国Ⅱ高考)如图,P是☉O外一点,PA是切线,A为切点,割线PBC与☉O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交☉O于点E.证明:
(1)BE=EC;
(2)AD·DE=2PB2.23415678证明:(1)连接AB,AC,
由题设知PA=PD,故∠PAD=∠PDA.
因为∠PDA=∠DAC+∠DCA,
∠PAD=∠BAD+∠PAB,∠DCA=∠PAB,
因此BE=EC.
(2)由切割线定理,得PA2=PB·PC.
因为PA=PD=DC,所以DC=2PB,BD=PB.
由相交弦定理,得AD·DE=BD·DC,
所以AD·DE=2PB2.
圆中的角有四类:圆心角、圆周角、弦切角和弧所对的角,与圆有关的角的计算与证明通常涉及这四类角,因此圆周角定理、圆心角定理和弦切角定理是解决此类问题的知识基础,通常利用圆周角、弦切角、圆心角与弧的关系来转化,并借助于圆内接四边形的对角互补和圆的切线垂直于经过切点的半径来解决.专题一专题二A.50° B.45° C.40° D.35° ∴∠CAE-∠ECA=10°.
又∠CEB=∠CAE+∠ACE=60°,
∴∠CAE=35°,即∠CAB=35°.
答案:C专题一专题二应用2如图,已知D,E分别是△ABC的BC,AC边上的点,且∠ADB=∠AEB.求证:∠CED=∠ABC.
提示:要证明∠CED=∠ABC,容易想到圆内接四边形的性质,需证明A,B,D,E四点共圆.用圆内接四边形的判定定理不易找到条件,故采用分类讨论来解决.专题一专题二证明:作△ABE的外接圆,则点D与外接圆有三种位置关系:①点D在圆外;②点D在圆内;③点D在圆上.
(1)如果点D在圆外,设BD与圆交于点F,连接AF,
如图.则∠AFB=∠AEB.而∠AEB=∠ADB,则
∠AFB=∠ADB.这与“三角形的外角大于任一
不相邻的内角”矛盾.故点D不能在圆外.
(2)如果点D在圆内,设圆与BD的延长线交于点F,连接AF,如图,
则∠AFB=∠AEB.
又因为∠AEB=∠ADB,
所以∠AFB=∠ADB.
这也与“三角形的外角大于任一不相邻的内角”矛盾.
故点D不可能在圆内.综上可得,点A,B,D,E在同一圆上.所以∠CED=∠ABC.专题一专题二专题二 与圆有关的线段的计算与证明
在圆中,解决与圆有关的线段的计算与证明问题时,先考虑圆幂定理,即相交弦定理、割线定理、切割线定理和切线长定理,得到成比例线段,再结合射影定理、相似三角形进行等比代换或等量代换加以证明或列出方程解得线段的长.专题一专题二应用3如图,过☉O外一点A作一条直线与☉O交于C,D两点,AB切☉O于点B,弦MN过CD的中点P.若AC=4,AB=6,则MP·NP= .?专题一专题二应用4在两圆公共弦AB上,任取一点G,过点G作直线交一圆于点C,D,交另一圆于点E,F.
求证:CG·ED=EG·CF.
提示:简单型的比例线段问题,首先考虑证明两个三角形相似.
证明:如图,连接AD,AE,BC,BF.
∵∠D=∠ABC,∠AGD=∠CGB,
∴△ADG∽△CBG.
∴AG·BG=CG·DG.①专题一专题二234156781(天津高考)如图,在圆O中,M,N是弦AB的三等分点,弦CD,CE分别经过点M,N.若CM=2,MD=4,CN=3,则线段NE的长为( )23415678解析:由相交弦定理,
因为M,N是弦AB的三等分点,
所以AM=MN=NB,MB=AN.
所以AM·MB=AN·NB.
答案:A23415678解析:由切割线定理得EC2=EB·EA,
即12=EB·(EB+4),可求得EB=2.
连接OC,则OC⊥DE,所以OC∥AD,答案:3 2(广东高考)如图,AB为圆O的直径,E为AB延长线上一点,过E作圆O的切线,切点为C,过A作直线EC的垂线,垂足为D.若AB=4,CE=234156783(重庆高考)如图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,PC=3,CE∶ED=2∶1,则BE= .?
解析:因为PA是圆的切线,
所以有PA2=PC·PD,
因此CD=PD-PC=9.
又因为CE∶ED=2∶1,所以CE=6,ED=3.
又由相交弦定理可得AE·BE=CE·ED,
答案:2234156784(广东高考)如图,已知AB是圆O的直径,AB=4,EC是圆O的切线,切点为C,BC=1,过圆心O作BC的平行线,分别交EC和AC于点D和点P,则OD= .?23415678答案:8 234156785(课标全国Ⅰ高考)如图,AB是☉O的直径,AC是☉O的切线,BC交☉O于点E.
(1)若D为AC的中点,证明:DE是☉O的切线;23415678解:(1)连接AE,由已知得,AE⊥BC,AC⊥AB.
在Rt△AEC中,由已知得,DE=DC,故∠DEC=∠DCE.
连接OE,则∠OBE=∠OEB.
又∠ACB+∠ABC=90°,
所以∠DEC+∠OEB=90°,
故∠OED=90°,DE是☉O的切线.234156786(课标全国Ⅱ高考)如图,O为等腰三角形ABC内一点,☉O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.
(1)证明:EF∥BC;
(2)若AG等于☉O的半径,且AE=MN=23415678解:(1)由于△ABC是等腰三角形,AD⊥BC,所以AD是∠CAB的平分线.
又因为☉O分别与AB,AC相切于点E,F,
所以AE=AF,故AD⊥EF.
从而EF∥BC.
(2)由(1)知,AE=AF,AD⊥EF,
故AD是EF的垂直平分线.
又EF为☉O的弦,所以O在AD上.
连接OE,OM,则OE⊥AE.23415678由AG等于☉O的半径得AO=2OE,
所以∠OAE=30°.
因此△ABC和△AEF都是等边三角形.234156787(课标全国Ⅰ高考)如图,四边形ABCD是☉O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
(1)证明:∠D=∠E;
(2)设AD不是☉O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.23415678(1)证明:由题设知A,B,C,D四点共圆,所以∠D=∠CBE.
由已知得∠CBE=∠E,故∠D=∠E.
(2)解:设BC的中点为N,连接MN,则由MB=MC,知MN⊥BC,故O在直线MN上.
又AD不是☉O的直径,M为AD的中点,
故OM⊥AD,即MN⊥AD.
所以AD∥BC,故∠A=∠CBE.
又∠CBE=∠E,故∠A=∠E.
由(1)知,∠D=∠E,所以△ADE为等边三角形.234156788(课标全国Ⅱ高考)如图,P是☉O外一点,PA是切线,A为切点,割线PBC与☉O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交☉O于点E.证明:
(1)BE=EC;
(2)AD·DE=2PB2.23415678证明:(1)连接AB,AC,
由题设知PA=PD,故∠PAD=∠PDA.
因为∠PDA=∠DAC+∠DCA,
∠PAD=∠BAD+∠PAB,∠DCA=∠PAB,
因此BE=EC.
(2)由切割线定理,得PA2=PB·PC.
因为PA=PD=DC,所以DC=2PB,BD=PB.
由相交弦定理,得AD·DE=BD·DC,
所以AD·DE=2PB2.
