22.1.4 二次函数y=ax2+bx+c的 图象和性质 第1课时 课件
文档属性
| 名称 | 22.1.4 二次函数y=ax2+bx+c的 图象和性质 第1课时 课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 10:25:03 | ||
图片预览


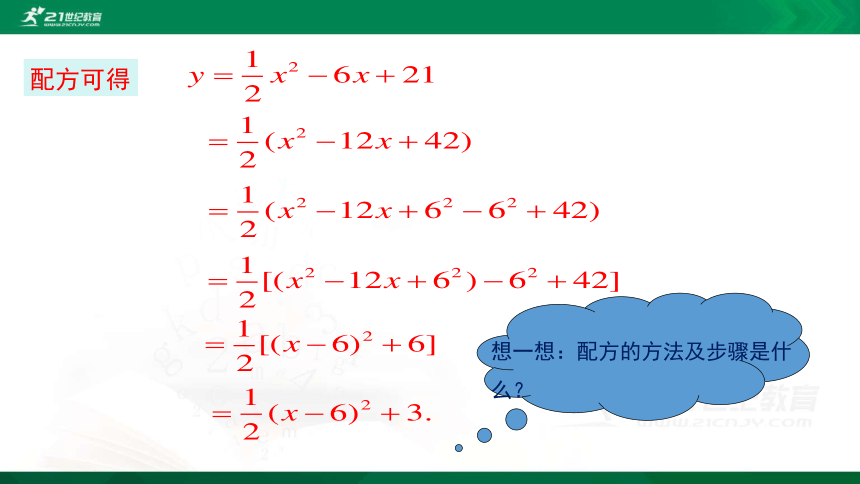
文档简介
(共18张PPT)
22.1.4二次函数y=ax2+bx+c的
图象和性质
第1课时 二次函数y=ax2+bx+c的图象和性质
导入新课
复习引入
向上
向下
(h ,k)
(h ,k)
x=h
x=h
当xh时,
y随着x的增大而增大.
当xh时,
y随着x的增大而减小.
x=h时,y最小=k
x=h时,y最大=k
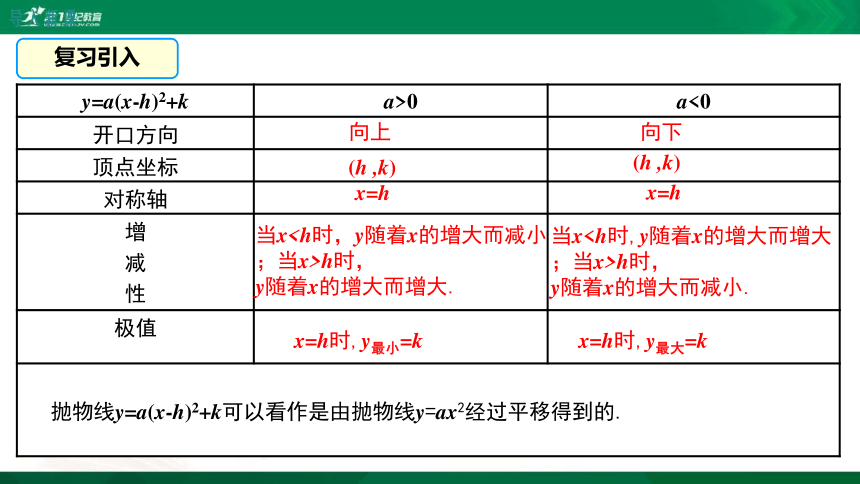
抛物线y=a(x-h)2+k可以看作是由抛物线y=ax2经过平移得到的.
y=a(x-h)2+k a>0 a<0
开口方向
顶点坐标
对称轴
增
减
性
极值
(0,0)
y轴
0
(0,-5)
y轴
-5
(-2,0)
直线x=-2
0
(-2,-4)
直线x=-2
-4
(4,3)
直线x=4
3
?
?
?
?
?
?
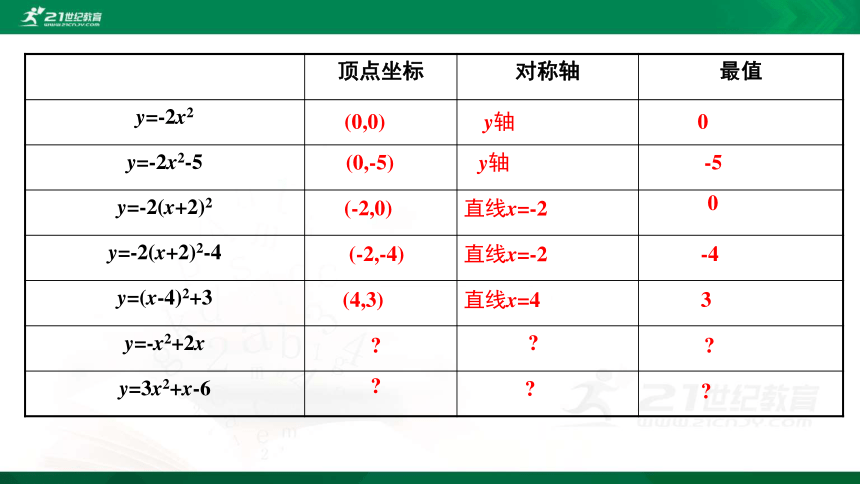
顶点坐标 对称轴 最值
y=-2x2
y=-2x2-5
y=-2(x+2)2
y=-2(x+2)2-4
y=(x-4)2+3
y=-x2+2x
y=3x2+x-6
讲授新课
探究归纳
配方可得
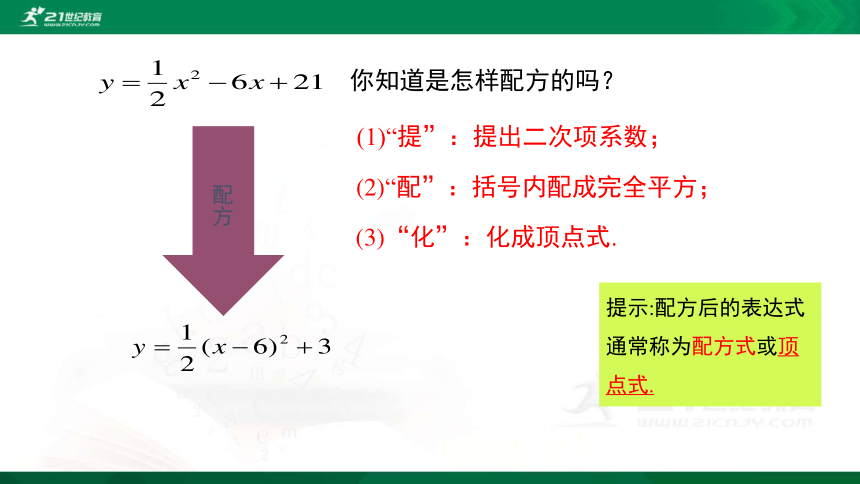
配方
你知道是怎样配方的吗?
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式.
提示:配方后的表达式通常称为配方式或顶点式.
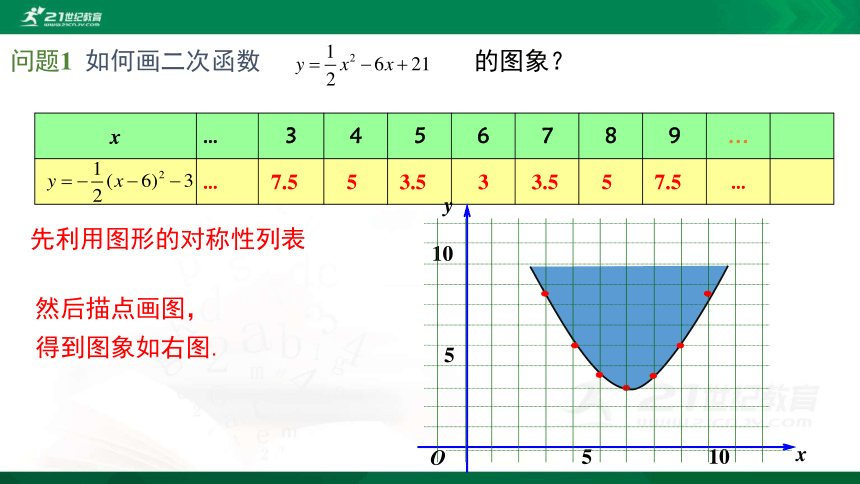
问题1 如何画二次函数 的图象?
先利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
然后描点画图,
得到图象如右图.
O
问题2 结合二次函数 的图象,说出其性质.
x=6
当x<6时,y随x的增大而减小;
当x>6时,y随x的增大而增大.
O
我们如何用配方法将一般式y=ax2+bx+c(a≠0)化成顶点式y=a(x-h)2+k?
y=ax?+bx+c
归纳总结
二次函数y=ax2+bx+c的图象和性质
(1)
(2)
如果a>0,当x< 时,y随x的增大而减小;当
x> 时,y随x的增大而增大.
如果a<0,当x< 时,y随x的增大而增大;当
x> 时,y随x的增大而减小.
填一填
(1,3)
x=1
最大值1
(0,-1)
y轴
最大值-1
最小值-6
顶点坐标 对称轴 最值
y=-x2+2x
y=-2x2-1
y=9x2+6x-5
1.已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
A.y轴 B.直线x=
C. 直线x=2 D.直线x=
则该二次函数图象的对称轴为( )
D
当堂练习
x -1 0 1 2 3
y 5 1 -1 -1 1
2.根据公式确定下列二次函数图象的对称轴和顶点坐标:
直线x=3
直线x=8
直线x=1.25
直线x= 0.5
课堂小结
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
配方法
公式法
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
22.1.4二次函数y=ax2+bx+c的
图象和性质
第1课时 二次函数y=ax2+bx+c的图象和性质
导入新课
复习引入
向上
向下
(h ,k)
(h ,k)
x=h
x=h
当x
y随着x的增大而增大.
当x
y随着x的增大而减小.
x=h时,y最小=k
x=h时,y最大=k
抛物线y=a(x-h)2+k可以看作是由抛物线y=ax2经过平移得到的.
y=a(x-h)2+k a>0 a<0
开口方向
顶点坐标
对称轴
增
减
性
极值
(0,0)
y轴
0
(0,-5)
y轴
-5
(-2,0)
直线x=-2
0
(-2,-4)
直线x=-2
-4
(4,3)
直线x=4
3
?
?
?
?
?
?
顶点坐标 对称轴 最值
y=-2x2
y=-2x2-5
y=-2(x+2)2
y=-2(x+2)2-4
y=(x-4)2+3
y=-x2+2x
y=3x2+x-6
讲授新课
探究归纳
配方可得
配方
你知道是怎样配方的吗?
(1)“提”:提出二次项系数;
(2)“配”:括号内配成完全平方;
(3)“化”:化成顶点式.
提示:配方后的表达式通常称为配方式或顶点式.
问题1 如何画二次函数 的图象?
先利用图形的对称性列表
7.5
5
3.5
3
3.5
5
7.5
然后描点画图,
得到图象如右图.
O
问题2 结合二次函数 的图象,说出其性质.
x=6
当x<6时,y随x的增大而减小;
当x>6时,y随x的增大而增大.
O
我们如何用配方法将一般式y=ax2+bx+c(a≠0)化成顶点式y=a(x-h)2+k?
y=ax?+bx+c
归纳总结
二次函数y=ax2+bx+c的图象和性质
(1)
(2)
如果a>0,当x< 时,y随x的增大而减小;当
x> 时,y随x的增大而增大.
如果a<0,当x< 时,y随x的增大而增大;当
x> 时,y随x的增大而减小.
填一填
(1,3)
x=1
最大值1
(0,-1)
y轴
最大值-1
最小值-6
顶点坐标 对称轴 最值
y=-x2+2x
y=-2x2-1
y=9x2+6x-5
1.已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
A.y轴 B.直线x=
C. 直线x=2 D.直线x=
则该二次函数图象的对称轴为( )
D
当堂练习
x -1 0 1 2 3
y 5 1 -1 -1 1
2.根据公式确定下列二次函数图象的对称轴和顶点坐标:
直线x=3
直线x=8
直线x=1.25
直线x= 0.5
课堂小结
顶点:
对称轴:
y=ax2+bx+c(a ≠0)
(一般式)
配方法
公式法
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
