沪科版八年级数学上册第14章全等三角形单元测试卷解析版
文档属性
| 名称 | 沪科版八年级数学上册第14章全等三角形单元测试卷解析版 |

|
|
| 格式 | zip | ||
| 文件大小 | 251.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-24 00:00:00 | ||
图片预览



文档简介
全等三角形单元测试卷
考试范围:14章;考试时间:120分钟;
一、单选题(每题4分共40分)
1.下列是利用了三角形的稳定性的有( )个
①自行车的三角形车架;
②长方形门框的斜拉条;
③照相机的三脚架;
④塔吊上部的三角形结构.
A.1??????????????????????????????????????B.2??????????????????????C.3??????????????????? D.4
2.如图,已知的3条边和3个角,则能判断和全等的是( )
A.甲和乙 B.乙和丙 C.只有乙 D.只有丙
3.△ABC≌△ADE,如果AB=5cm,BC=7cm,AC=6cm,那么DE的长是()
A.6cm B.5cm C.7cm D.无法确定
4.如图,在四边形ABCD中,AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有( )
A.3对 B.4对 C.2对 D.5对
5.下列三角形不一定全等的是( )
A.有两个角和一条边对应相等的三角形
B.有两条边和一个角对应相等的三角形
C.斜边和一锐角对应相等的两个直角三角形
D.三条边对应相等的两个三角形
6.如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线。此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE。则说明这两个三角形全等的依据是( )
A.SAS B.ASA C.AAS D.SSS
7.下列四组条件中, 能使△ABC≌△DEF的条件有( )
①AB = DE, BC = EF, AC = DF; ②AB = DE, ∠B = ∠E, BC = EF;
③∠B = ∠E, BC = EF, ∠C = ∠F; ④AB = DE, AC = DF, ∠B = ∠E.
A.1组 B.2组 C.3组 D.4组
8.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是( )
A.相等 B.互补 C.互补或相等 D.不相等
9.如图,已知△ABE≌△ACD,且∠B=∠C,则下列结论:(1)∠1=∠2;(2)∠BAD=∠CAE(3)AD=AE;(4)DB=EC.其中错误的个数为( )
A.0 B.1 C.2 D.3
10.如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△ACN≌△ABM.其中正确的结论是( )
A.①③④ B.②③④ C.①②③ D.①②④
二、填空题(每题5分共20分)
11.如图,∠B=∠D=90°,BC=DC,∠1=40°,则∠2=______°.
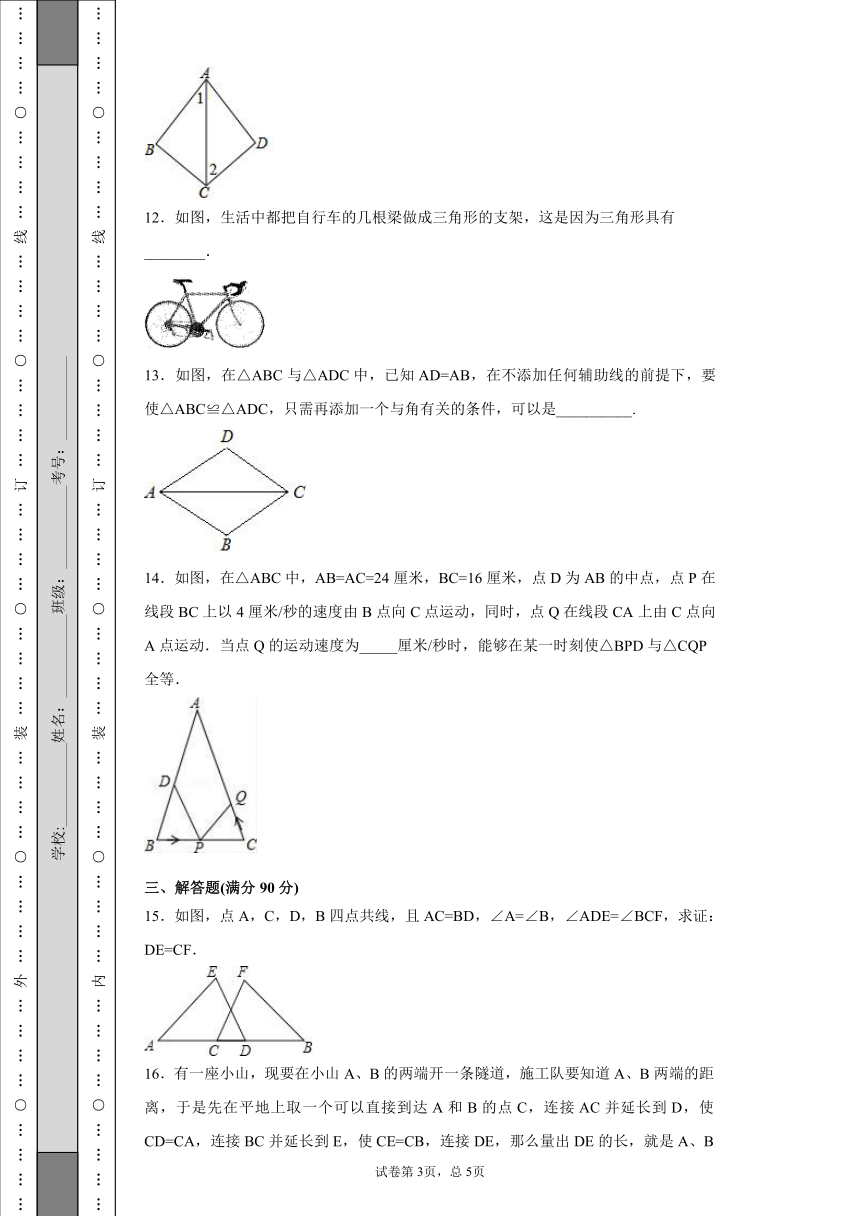
12.如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有________.
13.如图,在△ABC与△ADC中,已知AD=AB,在不添加任何辅助线的前提下,要使△ABC≌△ADC,只需再添加一个与角有关的条件,可以是__________.
14.如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_____厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
三、解答题(满分90分)
15.如图,点A,C,D,B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.
16.有一座小山,现要在小山A、B的两端开一条隧道,施工队要知道A、B两端的距离,于是先在平地上取一个可以直接到达A和B的点C,连接AC并延长到D,使CD=CA,连接BC并延长到E,使CE=CB,连接DE,那么量出DE的长,就是A、B的距离,请解释其中的道理。
17.如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)求证:△ABE≌△CBD;
(2)证明:∠1=∠3.
18.如图,已知∠1=∠2,∠3=∠4,EC=AD,求证:AB=BE.
19.已知:如图,∠A=∠D=90°,AC=BD.求证:OB=OC.
?
20.已知:如图,等腰直角三角形ABC中,∠A=90°,D为BC中点,E、F分别为AB、AC上的点,且满足EA=CF.链接AD,求证:DE=DF.
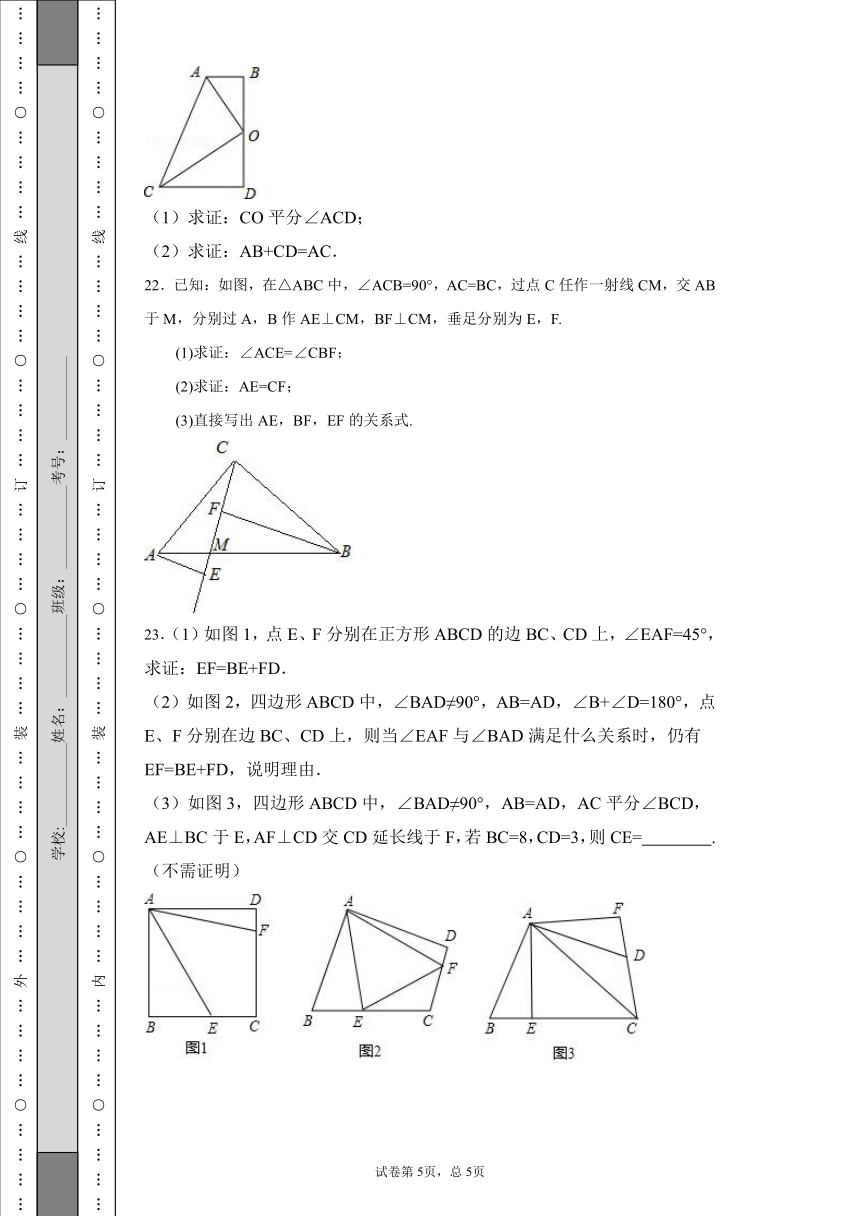
21.如图,四边形ABDC中,∠D=∠ABD=90°,点O为BD的中点,且OA⊥OC.
(1)求证:CO平分∠ACD;
(2)求证:AB+CD=AC.
22.已知:如图,在△ABC中,∠ACB=90°,AC=BC,过点C任作一射线CM,交AB于M,分别过A,B作AE⊥CM,BF⊥CM,垂足分别为E,F.
(1)求证:∠ACE=∠CBF;
(2)求证:AE=CF;
(3)直接写出AE,BF,EF的关系式.
23.(1)如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,求证:EF=BE+FD.
(2)如图2,四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD,说明理由.
(3)如图3,四边形ABCD中,∠BAD≠90°,AB=AD,AC平分∠BCD,AE⊥BC于E,AF⊥CD交CD延长线于F,若BC=8,CD=3,则CE= .(不需证明)
参考答案
1.D
【解析】
【分析】
只要三角形的三边确定,则三角形的大小唯一确定,即三角形的稳定性.
【详解】
①自行车的三角形车架,利用了三角形的稳定性; ②长方形门框的斜拉条,利用了三角形的稳定性; ③照相机的三脚架,利用了三角形的稳定性;④塔吊上部的三角形结构,利用了三角形的稳定性,
故利用了三角形稳定性的有4个,
故选D.
【点睛】
本题考查了三角形的特性:稳定性,应注意在实际生活中的应用.
2.B
【解析】
【分析】
甲只有2个已知条件,缺少判定依据;乙可根据SAS判定与△ABC全等;丙可根据AAS判定与△ABC全等,可得答案.
【详解】
解:甲三角形只知道一条边长、一个内角度数无法判断是否与△ABC全等;
乙三角形夹50°内角的两边分别与已知三角形对应相等,故乙与△ABC全等;
丙三角形72°内角及所对边与△ABC对应相等且均有50°内角,可根据AAS判定乙与△ABC全等;
则与△ABC全等的有乙和丙,
故选:B.
【点睛】
本题主要考查全等三角形的判定定理,熟练掌握并充分理解三角形全等的判定定理,注意对应二字的理解很重要.
3.C
【解析】
【分析】
根据全等三角形的书写,DE与BC是对应边,再根据全等三角形对应边相等即可求出DE的长度也就是BC的长度.
【详解】
解:∵△ABC≌△ADE,
∴DE=BC,
∵BC=7cm,
∴DE=7cm.
故选:C.
【点睛】
本题主要考查全等三角形的规范书写问题,全等三角形的对应顶点的字母要写在对应位置上,还考查了全等三角形对应边相等的性质.
4.A
【解析】
【分析】
利用全等三角形的判定即可解题,见详解.
【详解】
解:由图可知AC=AC
∵AB=AD,CB=CD,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,∠ACB=∠ACD,
△ABO≌△ADO(SAS), △CBO≌△CDO(SAS),
一共有三对全等,故选A.
【点睛】
本题考查了全等三角形的识别,属于简单题,熟悉全等三角形的判定方法是解题关键.
5.B
【解析】试题分析:根据全等三角形的判定:ASA或AAS可知:有两个角和一条边对应相等的两个三角形全等,故A不正确;
当有两边和一角对应相等的两三角形,只有当两边及其夹角对应相等时,即SAS,两三角形全等,故B正确;
根据一锐角对应相等时,直角和另一锐角也对应相等,故根据ASA或AAS可判断两三角形全等,故C不正确;
根据三边对应相等的两三角形全等(SSS),故D不正确.
故选:B.
点睛:此题主要考查了三角形全等的判定,解题关键是利用三角形全等的判定:SSS、SAS、AAS、ASA以及直角三角形的判定“HL”判断即可,注意解题时时刻要注意“对应”的应用.
6.D
【解析】
试题解析:在△ADC和△ABC中,
,
∴△ADC≌△ABC(SSS),
∴∠DAC=∠BAC,
即∠QAE=∠PAE.
故选D.
7.C
【解析】
【详解】
试题分析:①AB = DE, BC = EF, AC = DF,边边边;②AB = DE, ∠B = ∠E, BC = EF,边角边;③∠B = ∠E, BC = EF, ∠C = ∠F,角边角;故选C.
8.C
【解析】
【分析】
第三边所对的角即为前两边的夹角.分两种情况,一种是两个锐角或两个钝角三角形,另一种是一个钝角三角形和一个锐角三角形.
【详解】
第一种情况,当两个三角形全等时,是相等关系,
第二种情况,如图,AC=AC′,高CD=C′D′,∴∠ADC=∠AD′C′,
在Rt△ACD和Rt△AC′D′中,∵,
∴Rt△ACD≌Rt△AC′D′(HL),∴∠CAD=∠C′AD′,
此时,∠CAB+∠C′AB=180°,是互补关系.
所以选“相等或互补”.
故选C.
【点睛】
本题考查了全等三角形的性质,应注意的是,三角形高的位置,解题时要多方面考虑.
9.A
【解析】
【分析】
根据全等三角形的性质,全等三角形的对应边相等,全等三角形的对应角相等,即可进行判断.
【详解】
∵△ABE≌△ACD,且∠B=∠C,
∴∠1=∠2,BE=CD,AD=AE,∠BAE=∠CAD,
∴BE?DE=CD=DE,∠BAE?∠DAE=∠CAD?∠DAE,
即BD=CE,∠BAD=∠CAE,
故(1)(2)(3)(4)正确;
故答案选:A.
【点睛】
本题考查了全等三角形的性质,解题的关键是熟练的掌握全等三角形的性质.
10.A
【解析】
【分析】
根据题目中所给的大部分选项先判断该证明哪两个三角形全等,然后对各选项采取排除法得到正确选项.
【详解】
∵∠EAC=∠FAB,∴∠EAB=∠CAF.
又∵∠E=∠F=90°,AE=AF,∴△ABE≌△ACF,
∴∠B=∠C,BE=CF.
由△AEB≌△AFC知:∠B=∠C,AC=AB;
又∵∠CAB=∠BAC,∴△ACN≌△ABM;(故④正确)
由于条件不足,无法证得②CD=DN;故正确的结论有:①③④.
故选A.
【点睛】
本题考查了全等三角形的判定和性质,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
11.50°
【解析】试题解析:∵∠B=∠D=90°,
∴△ABC和△ADC均为直角三角形,
在RT△ABC和RT△ADC中,
,
∴RT△ABC≌RT△ADC(HL),
∴∠1=∠CAD,
∴∠2=90°-∠CAD=50°.
12.稳定性
【解析】
做成三角形的支架是应用了三角形的稳定性,因为三角形具有稳定性.
故答案为:稳定.
13.∠DAC=∠BAC或AC平分∠BAD
【解析】试题解析:一个与角有关的条件是:∠DAC=∠BAC或AC平分∠BAD.
14.4或6
【解析】
设经过x秒后,使△BPD与△CQP全等,
∵AB=AC=24厘米,点D为AB的中点,
∴BD=12厘米,
∵∠ABC=∠ACB,
∴要使△BPD与△CQP全等,必须BD=CP或BP=CP,
即12=16?4x或4x=16?4x,
解得:x=1或x=2,
x=1时,BP=CQ=4,4÷1=4;
x=2时,BD=CQ=12,12÷2=6;
即点Q的运动速度是4或6,
故答案为:4或6
点睛:本题考查了全等三角形的对应边相等的性质,等边对等角的性质,根据对应角分情况讨论是本题的难点.
15.证明见解析
【解析】
【分析】
根据条件可以求出AD=BC,再证明△AED≌△BFC,由全等三角形的性质就可以得出结论.
【详解】
∵AC=BD,
∴AC+CD=BD+CD,
∴AD=BC,
在△AED和△BFC中,
,
∴△AED≌△BFC(ASA),
∴DE=CF.
【点睛】
本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解题的关键.
16.理由见解析
【解析】试题分析:由题意知AC=DC,BD=EC,根据∠ACB=∠DCE即可证明△ABC≌△DEC,即可得AB=DE,即可解题.
试题解析:在△ABC和△DEC中,
AC=CD,∠ACB=∠ECD(对顶角),BC=EC,
∴△ABC≌△DEC,
∴AB=ED,
即量出DE的长,就是A、B的距离
【点睛】本题考查了全等三角形在实际生活中的应用,考查了全等三角形对应边相等的性质,本题中求证△ABC≌△DEC是解题的关键.
17.(1)证明见解析;(2)证明见解析
【解析】
试题分析:(1)由已知角相等,利用等式的性质得到,利用SAS即可得证;
(2)利用全等三角形对应角相等得到,再由及三角形内角和定理即可得证.
试题解析:,
,即,
在和中,
,
≌;
≌,
,
,
.
【点睛】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.
18.证明见解析
【解析】
试题分析:求线段相等,可把线段放进两个三角形中,求解三角形全等,由全等,即可得出线段相等.
试题解析:证明:∵∠1=∠2,
∴∠ABD=∠EBC,
∵∠3=∠4,
∴∠A=∠E,
又∵EC=AD,
∴△ABD≌△EBC.
∴AB=BE.
19.证明见解析.
【解析】
试题分析: ∵∠A=∠D=90°,AC=BD,BC=BC,∴Rt△BAC≌Rt△CDB.∴∠ACB=∠DBC,∴∠OCB=∠OBC,∴OB=OC(等角对等边).
考点:1.直角三角形全等的判定;2.等腰三角形的判定.
20.证明见解析
【解析】试题分析:根据等腰直角三角形的性质得到∠C=45°,中线AD平分∠BAC,并且AD=BC,则∠BAD=∠C,AD=DC,又EA=CF,根据全等三角形的判定易得到△ADE≌△CDF,然后根据全等三角形的性质即可得到结论.
试题解析:连接AD,如图,
∵△ABC为等腰直角三角形,D为BC中点,
∴AD=DC,AD平分∠BAC,∠C=45°,
∴∠EAD=∠C=45°,
在△ADE和△CDF中
,
∴△ADE≌△CDF,
∴DE=DF.
【点睛】本题考查了全等三角形的判定与性质:如果两个三角形中有两组对应边相等,并且它们所夹的角相等,那么这两个三角形全等;全等三角形的对应边相等.也考查了等腰直角三角形性质.
21.详见解析.
【解析】
试题分析:(1)延长AO交CD延长线于点E,通过证明△AOB≌△EOD可以得到AO=OE,从而证明△ACE为等腰三角形,再利用等腰三角形三线合一性质即可证明CO平分∠ACD;
(2)由第(1)问△AOB≌△EOD可得AB=DE,又因为AC=CE,AC=CD+DE=CD+AB.
试题解析:
(1)如图,延长AO交CD延长线于点E,
∵O为BD中点,∴BO=DO,
在△AOB和△EOD中,,
∴△AOB≌△EOD,
∴AO=AE,
∵OA⊥OC,
∴AC=CE,
∴CO平分∠ACD;
(2)∵△AOB≌△EOD,
∴AB=DE,
∵AC=CE,CE=CD+DE,
∴AC=CD+DE=CD+AB.
点睛:(1)题目中出现中点可以利用“倍长中线造全等”的方法构造全等三角形.
(2)要证明一条线段等于两条线段之和,可以采用“截长补短”的方法构造全等三角形证明.
22.(1)证明见解析;(2)证明见解析;(3)BF=AE+EF
【解析】(1)∵AE⊥CM.BF⊥CM,
∴∠AEC=∠BFC=∠ACB=90°,
∴∠CAE+∠ACE=90°,∠ACE+∠BCF=90°,
∴∠CAE=∠BCF,
在△ACE和△CBF中, ,
∴△ACE≌△CBF,∴∠ACE=∠CBF.
(2)∵△ACE≌△CBF,∴AE=CF.
(3)结论:BF=AE+EF.
∵△ACE≌△CBF,∴AE=CF,CE=BF,
∴BF=EF+CF=EF+AE.
23.(1)详见解析;(2)∠BAD=2∠EAF,理由详见解析;(3)CE=5.5.
【解析】试题分析:(1)将△ABE绕点A旋转使得AB与AD重合,然后证明△AFG≌△AFE,再利用全等三角形对应的边相等的性质不难证明;(2)首先延长CB至M,使BM=DF,连接AM,构造△ABM≌△ADF,再证明△FAE≌△MAE,最后将相等的边进行转化整理即可证明.
试题解析:
(1)证明:把△ABE绕点A逆时针旋转90°至△ADG,如图1所示:
则△ADG≌△ABE,
∴AG=AE,∠DAG=∠BAE,DG=BE,
又∵∠EAF=45°,即∠DAF+∠BAE=∠EAF=45°,
∴∠GAF=∠FAE,
在△GAF和△FAE中, , ,
∴△AFG≌△AFE(SAS).
∴GF=EF.
又∵DG=BE,
∴GF=BE+DF,
∴BE+DF=EF.
(2)∠BAD=2∠EAF.理由如下:
如图2所示,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中, ,
∴△ABM≌△ADF(SAS)
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中, ,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
(3)CE=5.5
点睛:(1)在出现正方形或者等腰直角三角形的题目中,我们多采用旋转构造全等三角形的方法.
(2)遇到此类压轴题,第一问的思路方法可以为第二问、第三问所用.
试卷第4页,总5页
试卷第3页,总5页
