21.2.1配方法 第2课时 课件

(共23张PPT)
21.2 解一元二次方程
21.2.1 配方法
第二十一章 一元二次方程




课程讲授





















新知导入







随堂练习




课堂小结
第2课时 配方法
知识要点
1.用配方法解二次项系数为1的一元二次方程
2.用配方法解二次项系数不为1的一元二次方程
3.配方法的应用
新知导入
试一试：根据所学知识，完成下面的问题。
(1) 9x2+6x +1=( )2；
3x+1
(2) 9x2+6x-8= ( )2-_____；
(3) 9x2+6x -8=0；
( )2-_____=0；
( )2=_____；
3x+1
9
3x+1
3x+1
9
9
_____=_____；
3x+1
±3
x1=_____，x2=_____.
3
2
3
4
-
课程讲授
1
用配方法解二次项系数为1的一元二次方程
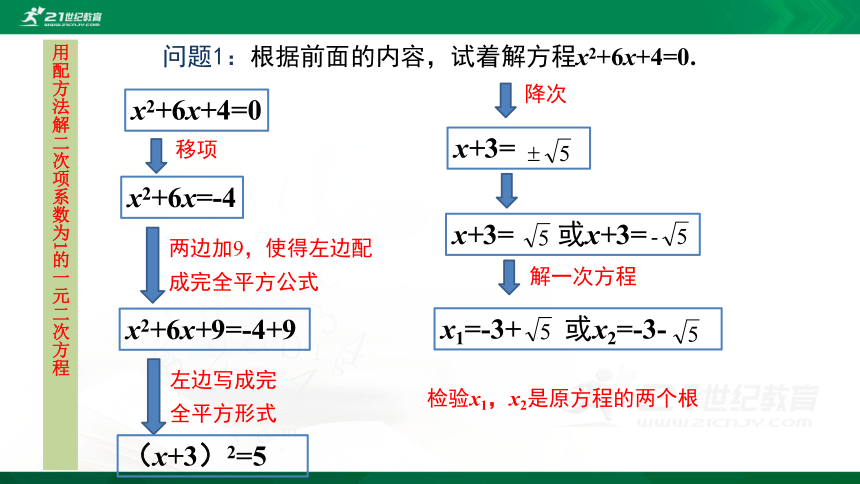
问题1：根据前面的内容，试着解方程x2+6x+4=0.
x2+6x+4=0

移项
x2+6x=-4

两边加9，使得左边配成完全平方公式
x2+6x+9=-4+9

左边写成完全平方形式
（x+3）2=5

降次
x+3=

x+3= 或x+3=

解一次方程
x1=-3+ 或x2=-3-
检验x1，x2是原方程的两个根
课程讲授
1
用配方法解二次项系数为1的一元二次方程
定义：通过配成完全平方式来解一元二次方程的方法，叫做配方法.
归纳：把方程化为（x+n)2=p的形式，将一元二次方程降次，转化为一元一次方程求解．
课程讲授
1
用配方法解二次项系数为1的一元二次方程
例 解方程x2-8x+1=0.
提示：方程的二次项系数为1，可以直接运用配方法。
解 移项，得
x2－8x=－1.
配方，得
x2－8x+42=－1+42 ,
( x－4)2=15
由此可得
课程讲授
1
用配方法解二次项系数为1的一元二次方程
练一练：用配方法解一元二次方程x2-6x-4=0，下列变形正确的是( )
A.（x-6）2=-4+36
B.（x-6）2=4+36
C.（x-3）2=-4+9
D.（x-3）2=4+9
D
课程讲授
2
用配方法解二次项系数不为1的一元二次方程
问题1：根据前面所学的知识试着解方程2x2+1=3x.
提示：先把方程转化为2x2-3x+1=0，它的二次项系数为2，为了方便配方，需要将二次项系数化为1，不能直接运用配方法。
课程讲授
2
用配方法解二次项系数不为1的一元二次方程
问题1：根据前面所学的知识试着解方程2x2+1=3x.
解 移项，得
2x2－3x=－1,
二次项系数化为1，得
x2－ x=－ ,
2
3
2
1
配方，得
x2－ x+（ ）2=－ +（ ）2 ,
2
3
2
1
4
3
4
3
（ x－ ）2= ,
4
3
16
1
由此可得
x－ = ± ,
4
3
4
1
x1= 1，x2= .
2
1
课程讲授
2
用配方法解二次项系数不为1的一元二次方程
例 解方程3x2-6x+4=0.
解 移项，得
3x2-6x=-4.
二次项系数化为1，得
x2-2x=- .
3
4
配方，得
x2-2x+12=- +12 .
3
4
（x-1）2=- +1.
3
4
（x-1）2=- .
3
1
因为实数的平方不会是负数，所以x取任何实数时，上式都不成立，所以原方程无实数根．
课程讲授
2
用配方法解二次项系数不为1的一元二次方程
练一练：用配方法解方程3x2-6x-1=0，则方程可变形为( )
A.(x-3)2=
B.(x-1)2=
C.(3x-1)2=
D.(x-1)2=
D
课程讲授
3
配方法的应用
例 用配方法证明：不论x为何值，-2x2+8x-11的值总小于0.
解 -2x2+8x-11
即不论x为何值，-2x2+8x-11的值总小于0.
=-2(x2-4x)-11
=-2(x2-4x+4)-11+8
=-2(x-2)2-3.
∵(x-2)2≥0,
∴-2(x-2)2≤0,
∴-2(x-2)2-3<0.
课程讲授
3
配方法的应用
练一练：用配方法求最值:
(1) 2x2 - 4x+6的最小值；

(2) -3x2 +6x +1的最大值.
解： 2x2 - 4x+6 = 2(x - 1)2 +4
当x =1时,2x2 - 4x+6有最小值4
解： -3x2 + 6x +1= -3(x - 1)2 + 4
当x =1时,有最大值4
课程讲授
3
配方法的应用
一般地，对于方程（x+n）2=p：
（1）当p>0时，方程_________________根，即_____________________。
（2）当p=0时，方程_________________根，即_______________。
（3）当p<0时，方程________根。
有两个不等的实数
有两个相等的实数
=0
无实数
随堂练习
1.一元二次方程y2-y- =0配方后可化为（ ）
A.
B.
C.
D.
B
随堂练习
2.若x2-4x+p=(x+q)2，则p，q的值分别是（ ）
A.p=4,q=2 B.p=4,q=-2
C.p=-4,q=2 D.p=-4,q=-2
3.若方程4x2-(m-2)x+1=0的左边是一个完全平方式，则m等于（ ）
A.-2
B.-2或6
C.-2或-6
D.2或-6
B
B
随堂练习
4.将方程x2－2x＝2配方成(x＋a)2＝k的形式，则方程的两边需加上_____.
1
5.如图，在一块长35m、宽26m的矩形地面上，修建同样宽的两条互相垂直的道路，剩余部分栽种花草，要使剩余部分的面积为850m2，道路的宽应为_______m.



1
随堂练习
6.三角形的两边长分别为3和6，第三边的长是方程x2-6x+8=0的解，则此三角形周长是_______.
7.已知点（5-k2，2k+3）在第四象限，且在其角平分线上，则k=_____.
-2
13
y
O
x
（5-k2，2k+3）

随堂练习
8.用配方法解下列方程:
(1)x2+8x-9=0；
（x+4）2=25
x2+8x=9
解 移项，得
配方，得
x2+8x+16=9+16
由此可得
x+4=±5
x1=1，x2=-9.
随堂练习
(2)3x2-1=2x.
解 移项，得
3x2-2x=1.
二次项系数化为1，得
配方，得
x2- x= .
3
1
2
3
x2- x+（ ）2= +（ ）2.
3
1
2
3
3
1
3
1
（x- ）2 = .
9
4
3
1
由此可得
x－ = ± ,
3
1
3
2
x1= 1，x2=- .
3
1
课堂小结
配方法

定义

通过配成完全平方式来解一元二次方程的方法，叫做配方法.
解二次项系数为1的一元二次方程
解二次项系数不为1的一元二次方程


应用
1.移项
2.配平方
3.开平方（降次）
4.解一次方程
1.移项
2.化二次项系数为1
3.配平方
4.开平方（降次）
5.解一次方程
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php