22.1.2二次函数y=ax2的图象和性质 课件
文档属性
| 名称 | 22.1.2二次函数y=ax2的图象和性质 课件 |  | |
| 格式 | rar | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-24 16:04:04 | ||
图片预览





文档简介
(共26张PPT)
22.1 二次函数的图象和性质
22.1.2 二次函数y=ax2的图象和
性质
第二十二章 二次函数
课程讲授
新知导入
随堂练习
课堂小结
知识要点
1.二次函数y=ax2的图象
2.二次函数y=ax2的性质
新知导入
看一看:观察下列运动,试着发现它们的规律。
课程讲授
1
二次函数y=ax2的图象
问题1.1:根据所学知识,试着画出二次函数y=x2的图像。
在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
9
4
1
0
1
9
4
课程讲授
1
二次函数y=ax2的图象
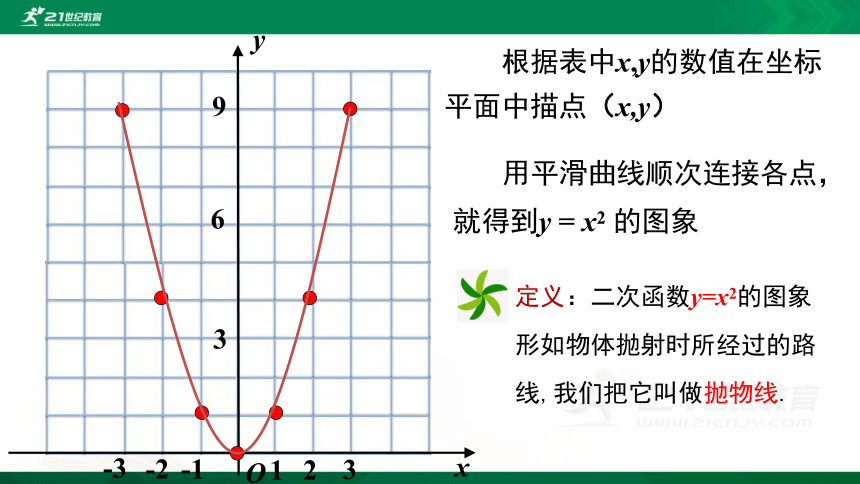
根据表中x,y的数值在坐标平面中描点(x,y)
-1
-2
-3
9
3
6
1
2
3
y
O
x
用平滑曲线顺次连接各点,就得到y = x2 的图象
定义:二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.
课程讲授
1
二次函数y=ax2的图象
-1
-2
-3
9
3
6
1
2
3
y
O
x
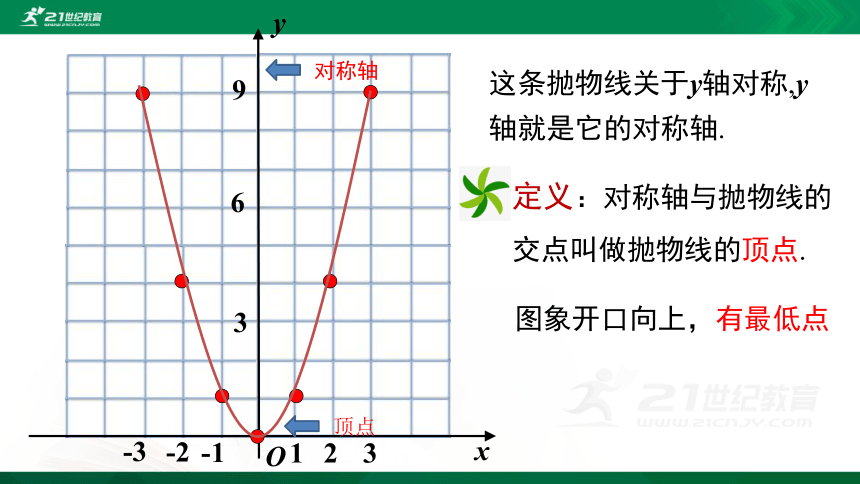
这条抛物线关于y轴对称,y轴就是它的对称轴.
对称轴
定义:对称轴与抛物线的交点叫做抛物线的顶点.
顶点
图象开口向上,有最低点
课程讲授
1
二次函数y=ax2的图象
问题1.2:根据所学知识,画出二次函数y=-x2的图像。
在y = -x2 中自变量x可以是任意实数,列表表示几组对应值:
x … -3 -2 -1 0 1 2 3 …
y=-x2 … …
-9
-4
-1
0
-1
-9
-4
课程讲授
-1
-2
-3
-4
-6
3
-9
-5
1
2
-3
4
5
y
O
x
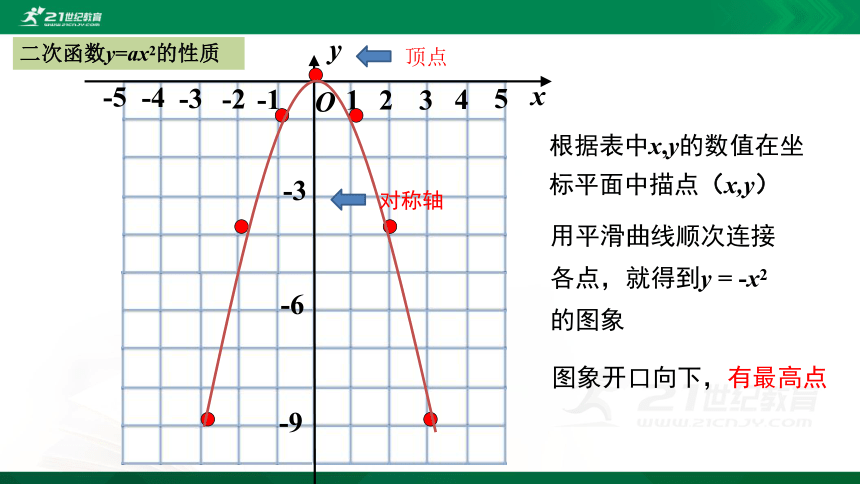
根据表中x,y的数值在坐标平面中描点(x,y)
用平滑曲线顺次连接各点,就得到y = -x2 的图象
2
二次函数y=ax2的性质
对称轴
顶点
图象开口向下,有最高点
课程讲授
-1
-2
-3
-4
-6
3
-9
-5
1
2
-3
4
5
y
O
x
2
二次函数y=ax2的性质
-1
-2
-3
9
3
6
1
2
3
y
O
x
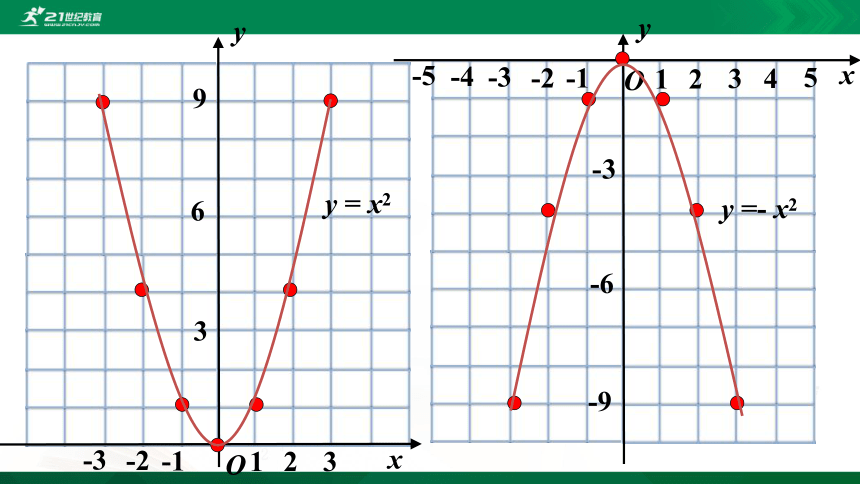
y = x2
y =- x2
课程讲授
1
二次函数y=ax2的图象
练一练:如图,函数y=2x2的图象大致为( )
C
课程讲授
2
二次函数y=ax2的性质
问题1:根据y=x2和y=-x2的图像,试着探究二次函数y=ax2的性质.
-1
-2
-3
-4
5
1
-2
3
-4
-5
-1
2
-3
4
-5
1
2
3
4
5
y
O
x
y = x2
y =- x2
对称轴都是y轴
共同点:
顶点都是坐标原点
不同点:
当a>0时,开口向上;
当a<0时,开口向下.
课程讲授
2
二次函数y=ax2的性质
-1
-2
-3
-4
5
1
-2
3
-4
-5
-1
2
-3
4
-5
1
2
3
4
5
y
O
x
对于抛物线 y = ax 2 (a>0)
当x>0时,y随x取值的增大而增大;
当x<0时,y随x取值的增大而减小.
当x<0时,y随x取值的增大而增大.
对于抛物线 y = ax 2 (a<0)
当x>0时,y随x取值的增大而减小;
课程讲授
2
二次函数y=ax2的性质
问题2:在同一直角坐标系中,画出函数
的图象.
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
… …
y=2x2 … …
9
4
1
0
1
9
4
2
0.5
0
4.5
2
0.5
4.5
8
2
0
8
0.5
18
18
课程讲授
-1
-2
-3
9
3
6
1
2
3
y
O
x
2
二次函数y=ax2的性质
y=x2
y=2x2
当a>0时,a越大,开口越小.
课程讲授
2
二次函数y=ax2的性质
问题3:在同一直角坐标系中,画出函数
的图象.
x … -3 -2 -1 0 1 2 3 …
y=-x2 … …
… …
y=-2x2 … …
-9
-4
-1
0
-1
-9
-4
-2
-0.5
0
-4.5
-2
-0.5
-4.5
-8
-2
0
-8
-0.5
-18
-18
课程讲授
2
二次函数y=ax2的性质
-1
-2
-3
-4
-6
3
-9
-5
1
2
-3
4
5
y
O
x
y=-x2
y=-2x2
当a<0时,a越大,开口越大.
课程讲授
2
二次函数y=ax2的性质
二次函数y=ax2的性质:
(1)当a>0时,开口_____,顶点是抛物线的最____点,a越大,开口越____,x>0时,y随x取值的__________,当x<0时,y随x取值的___________;
(2)当a<0时,开口_____,顶点是抛物线的最____点,a越大,开口越____,x>0时,y随x取值的__________,当x<0时,y随x取值的___________.
低
向上
小
向下
高
大
增大而增大
增大而减小
增大而减小
增大而增大
课程讲授
2
二次函数y=ax2的性质
练一练:抛物线y=2x2,y=-2x2,y=x2的共同性质是( )
A.开口向上
B.对称轴是y轴
C.都有最高点
D.y随x的增大而增大
B
随堂练习
1.若点(x1,y1),(x2,y2)是二次函数y=-4x2图象上两点,且x1>x2>0,则y1与y2的大小关系是( )
A.y1>y2 B.y1<y2
C.y1≥y2 D.y1≤y2
2.已知抛物线y=ax2(a>0)过点A(-2,y1),点B(1,y2),则下列关系式一定成立的是( )
A.y1>0>y2 B.y2>0>y1
C.y1>y2>0 D.y1≤y2
B
C
随堂练习
3.如图,从y=-x2的图象上可看出当-3A.-9B.-9≤y<-1
C.-9≤y≤0
D.-9D
随堂练习
4.如图,在同一坐标系中,作出①y=3x2,②y= x2,③y=x2的图象,则图象中从里到外的三条抛物线对应的函数依次是____________.(填序号)
①③②
随堂练习
5.二次函数y=ax2的图象如图所示.
(1)求这个二次函数解析式;
(2)若另一函数图象与该函数图象关于x轴对称,试求另一个函数的解析式.
解 (1)因为图象经过(2,2),代入解析式,
得a= ,
2
1
y=- x2.
2
1
故所求的解析式为y= x2.
2
1
(2)由题意得另一个函数的解析式为
随堂练习
6.二次函数y=ax2的图象与直线y=2x-1相交于点P(1,m).
(1)求a,m的值;
(2)写出二次函数的表达式,并指出x取何值时,该表达式的y随x的增大而增大;
(3)指出抛物线的顶点坐标和对称轴.
(3)顶点坐标为(0,0),对称轴为y轴.
解 (1)将(1,m)代入y=2x-1,
得m=2×1-1=1.
所以点P的坐标为(1,1),
将点P的坐标(1,1)代入y=ax2,得
1=a×12,
解得a=1.
(2)二次函数的表达式为y=x2,
当x>0时,y随x的增大而增大.
课堂小结
二次函数y=ax2的图象及性质
图象及性质
对于抛物线 y = ax 2 (a>0),开口向上
当x>0时,y随x取值的增大而增大;
当x<0时,y随x取值的增大而减小.
对于抛物线 y = ax 2 (a<0),开口向下
当x>0时,y随x取值的增大而减小;
当x<0时,y随x取值的增大而增大.
特性
对于抛物线 y = ax 2 ,|a|越大,抛物线的开口越小.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
22.1 二次函数的图象和性质
22.1.2 二次函数y=ax2的图象和
性质
第二十二章 二次函数
课程讲授
新知导入
随堂练习
课堂小结
知识要点
1.二次函数y=ax2的图象
2.二次函数y=ax2的性质
新知导入
看一看:观察下列运动,试着发现它们的规律。
课程讲授
1
二次函数y=ax2的图象
问题1.1:根据所学知识,试着画出二次函数y=x2的图像。
在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
9
4
1
0
1
9
4
课程讲授
1
二次函数y=ax2的图象
根据表中x,y的数值在坐标平面中描点(x,y)
-1
-2
-3
9
3
6
1
2
3
y
O
x
用平滑曲线顺次连接各点,就得到y = x2 的图象
定义:二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.
课程讲授
1
二次函数y=ax2的图象
-1
-2
-3
9
3
6
1
2
3
y
O
x
这条抛物线关于y轴对称,y轴就是它的对称轴.
对称轴
定义:对称轴与抛物线的交点叫做抛物线的顶点.
顶点
图象开口向上,有最低点
课程讲授
1
二次函数y=ax2的图象
问题1.2:根据所学知识,画出二次函数y=-x2的图像。
在y = -x2 中自变量x可以是任意实数,列表表示几组对应值:
x … -3 -2 -1 0 1 2 3 …
y=-x2 … …
-9
-4
-1
0
-1
-9
-4
课程讲授
-1
-2
-3
-4
-6
3
-9
-5
1
2
-3
4
5
y
O
x
根据表中x,y的数值在坐标平面中描点(x,y)
用平滑曲线顺次连接各点,就得到y = -x2 的图象
2
二次函数y=ax2的性质
对称轴
顶点
图象开口向下,有最高点
课程讲授
-1
-2
-3
-4
-6
3
-9
-5
1
2
-3
4
5
y
O
x
2
二次函数y=ax2的性质
-1
-2
-3
9
3
6
1
2
3
y
O
x
y = x2
y =- x2
课程讲授
1
二次函数y=ax2的图象
练一练:如图,函数y=2x2的图象大致为( )
C
课程讲授
2
二次函数y=ax2的性质
问题1:根据y=x2和y=-x2的图像,试着探究二次函数y=ax2的性质.
-1
-2
-3
-4
5
1
-2
3
-4
-5
-1
2
-3
4
-5
1
2
3
4
5
y
O
x
y = x2
y =- x2
对称轴都是y轴
共同点:
顶点都是坐标原点
不同点:
当a>0时,开口向上;
当a<0时,开口向下.
课程讲授
2
二次函数y=ax2的性质
-1
-2
-3
-4
5
1
-2
3
-4
-5
-1
2
-3
4
-5
1
2
3
4
5
y
O
x
对于抛物线 y = ax 2 (a>0)
当x>0时,y随x取值的增大而增大;
当x<0时,y随x取值的增大而减小.
当x<0时,y随x取值的增大而增大.
对于抛物线 y = ax 2 (a<0)
当x>0时,y随x取值的增大而减小;
课程讲授
2
二次函数y=ax2的性质
问题2:在同一直角坐标系中,画出函数
的图象.
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
… …
y=2x2 … …
9
4
1
0
1
9
4
2
0.5
0
4.5
2
0.5
4.5
8
2
0
8
0.5
18
18
课程讲授
-1
-2
-3
9
3
6
1
2
3
y
O
x
2
二次函数y=ax2的性质
y=x2
y=2x2
当a>0时,a越大,开口越小.
课程讲授
2
二次函数y=ax2的性质
问题3:在同一直角坐标系中,画出函数
的图象.
x … -3 -2 -1 0 1 2 3 …
y=-x2 … …
… …
y=-2x2 … …
-9
-4
-1
0
-1
-9
-4
-2
-0.5
0
-4.5
-2
-0.5
-4.5
-8
-2
0
-8
-0.5
-18
-18
课程讲授
2
二次函数y=ax2的性质
-1
-2
-3
-4
-6
3
-9
-5
1
2
-3
4
5
y
O
x
y=-x2
y=-2x2
当a<0时,a越大,开口越大.
课程讲授
2
二次函数y=ax2的性质
二次函数y=ax2的性质:
(1)当a>0时,开口_____,顶点是抛物线的最____点,a越大,开口越____,x>0时,y随x取值的__________,当x<0时,y随x取值的___________;
(2)当a<0时,开口_____,顶点是抛物线的最____点,a越大,开口越____,x>0时,y随x取值的__________,当x<0时,y随x取值的___________.
低
向上
小
向下
高
大
增大而增大
增大而减小
增大而减小
增大而增大
课程讲授
2
二次函数y=ax2的性质
练一练:抛物线y=2x2,y=-2x2,y=x2的共同性质是( )
A.开口向上
B.对称轴是y轴
C.都有最高点
D.y随x的增大而增大
B
随堂练习
1.若点(x1,y1),(x2,y2)是二次函数y=-4x2图象上两点,且x1>x2>0,则y1与y2的大小关系是( )
A.y1>y2 B.y1<y2
C.y1≥y2 D.y1≤y2
2.已知抛物线y=ax2(a>0)过点A(-2,y1),点B(1,y2),则下列关系式一定成立的是( )
A.y1>0>y2 B.y2>0>y1
C.y1>y2>0 D.y1≤y2
B
C
随堂练习
3.如图,从y=-x2的图象上可看出当-3
C.-9≤y≤0
D.-9
随堂练习
4.如图,在同一坐标系中,作出①y=3x2,②y= x2,③y=x2的图象,则图象中从里到外的三条抛物线对应的函数依次是____________.(填序号)
①③②
随堂练习
5.二次函数y=ax2的图象如图所示.
(1)求这个二次函数解析式;
(2)若另一函数图象与该函数图象关于x轴对称,试求另一个函数的解析式.
解 (1)因为图象经过(2,2),代入解析式,
得a= ,
2
1
y=- x2.
2
1
故所求的解析式为y= x2.
2
1
(2)由题意得另一个函数的解析式为
随堂练习
6.二次函数y=ax2的图象与直线y=2x-1相交于点P(1,m).
(1)求a,m的值;
(2)写出二次函数的表达式,并指出x取何值时,该表达式的y随x的增大而增大;
(3)指出抛物线的顶点坐标和对称轴.
(3)顶点坐标为(0,0),对称轴为y轴.
解 (1)将(1,m)代入y=2x-1,
得m=2×1-1=1.
所以点P的坐标为(1,1),
将点P的坐标(1,1)代入y=ax2,得
1=a×12,
解得a=1.
(2)二次函数的表达式为y=x2,
当x>0时,y随x的增大而增大.
课堂小结
二次函数y=ax2的图象及性质
图象及性质
对于抛物线 y = ax 2 (a>0),开口向上
当x>0时,y随x取值的增大而增大;
当x<0时,y随x取值的增大而减小.
对于抛物线 y = ax 2 (a<0),开口向下
当x>0时,y随x取值的增大而减小;
当x<0时,y随x取值的增大而增大.
特性
对于抛物线 y = ax 2 ,|a|越大,抛物线的开口越小.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
