23.1图形的旋转 第1课时 课件

(共20张PPT)
23.1 图形的旋转
第二十三章 旋转




课程讲授





















新知导入







随堂练习




课堂小结
第1课时 旋转的概念及性质
知识要点
1.旋转的认识
2.旋转的性质
新知导入
看一看：观察下图中图形的运动，试着发现它们的规律。
课程讲授
1
旋转的认识
问题1：根据前面的观察，风车风轮的每个叶片在风的吹动下转到到新的位置。这些现象有什么共同特点？
定义：像这样，在平面内，把一个图形绕一个定点按某个方向转动一个角度，这样的图形运动称为旋转.这个定点称为旋转中心.转动的角称为旋转角.
O
1
旋转的认识
归纳：
确定一次图形的旋转时,必须明确_________、__________、_____________.
旋转中心
旋转角
旋转方向
1
旋转的认识
练一练：下列属于旋转现象的是( )
A.空中落下的物体
B.雪橇在雪地里滑动
C.拧开水龙头的过程
D.火车在急刹车时向前滑动
C
1
旋转的认识





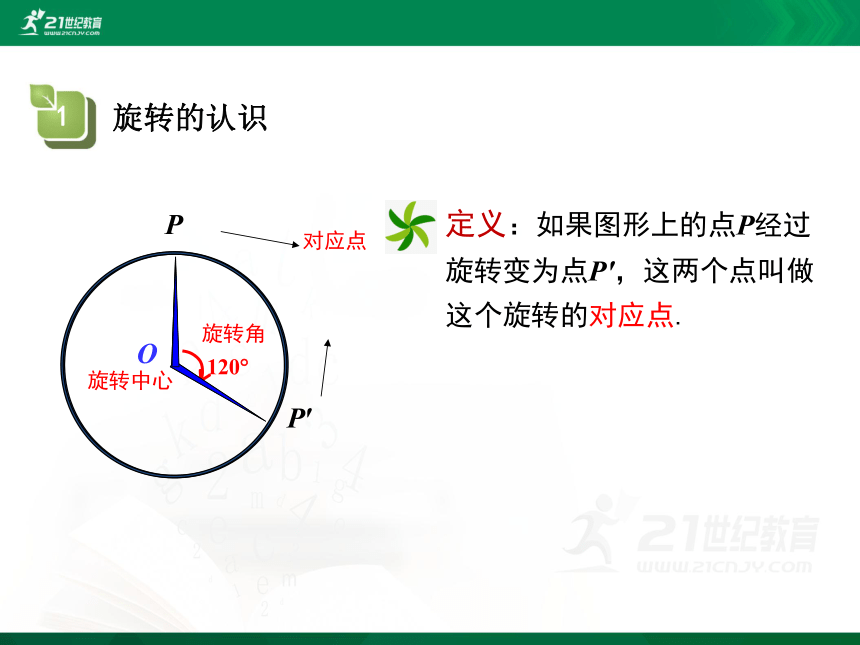
O
P′
P




旋转中心
旋转角
对应点



定义：如果图形上的点P经过旋转变为点P'，这两个点叫做这个旋转的对应点.
1
旋转的认识
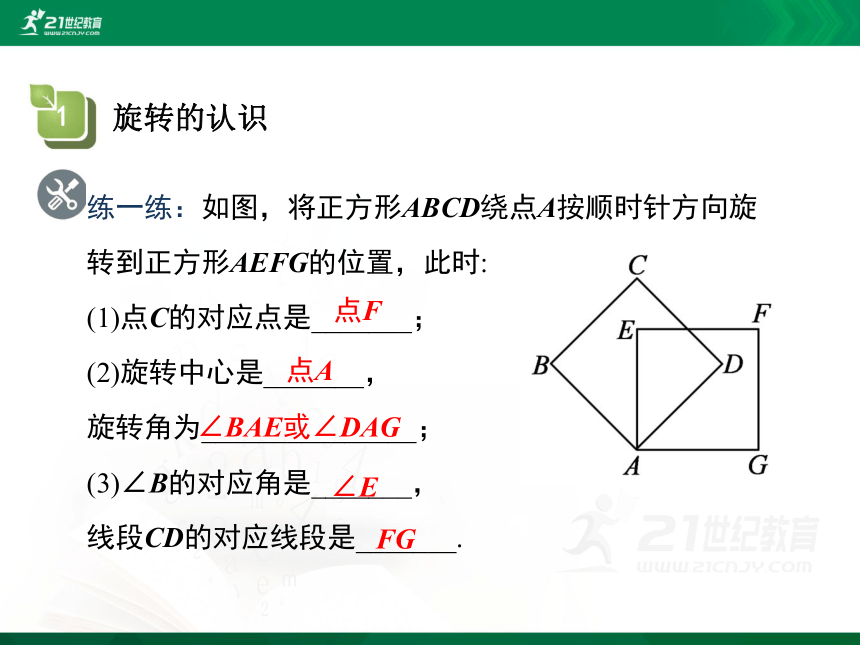
练一练：如图，将正方形ABCD绕点A按顺时针方向旋转到正方形AEFG的位置，此时:
(1)点C的对应点是_______；
(2)旋转中心是_______，
旋转角为_______________；
(3)∠B的对应角是_______，
线段CD的对应线段是_______.
点F
点A
∠BAE或∠DAG
∠E
FG
2
旋转的性质
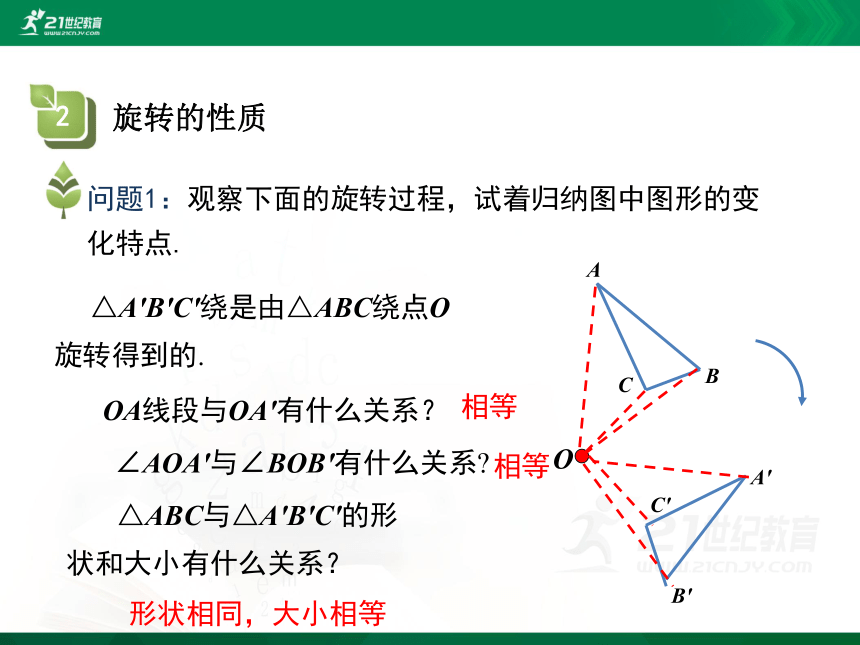
问题1：观察下面的旋转过程，试着归纳图中图形的变化特点.
C
A
B

O
C'
A'
B'

△ABC与△A'B'C'的形状和大小有什么关系？
△A'B'C'绕是由△ABC绕点O旋转得到的.
OA线段与OA'有什么关系？
相等
∠AOA'与∠BOB'有什么关系?
相等
形状相同，大小相等
2
旋转的性质
旋转的性质：
1.对应点到旋转中心的距离_____.
2.对应点与旋转中心所连的线段的夹角等于______.
3.旋转前后的图形______.
相等
旋转角
全等
2
旋转的性质
练一练：如图，在△ABC中，AB=8，AC=6，∠BAC=30°，将△ABC绕点A逆时针旋转60°得到△AB1C1，连接BC1，则BC1的长为（ ）
A.6
B.8
C.10
D.12
C
随堂练习
1.将如图所示的图案以圆心为中心，旋转180°后得到的图案是（ ）
D
2.如图，将△ABC绕点C顺时针旋转90°得到△EDC.若点A，D，E在同一条直线上，∠ACB=20°，则∠ADC的度数是（ ）
A.55°
B.60°
C.65°
D.70°
C
3.下列四个圆形图案中，分别以它们所在圆的圆心为旋转中心，顺时针旋转120°后，能与原图形完全重合的是( )
A
4.如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连接BB′，若∠A′B′B=20°，则∠A的度数是__________.
5.如图，在矩形ABCD中，AD=3，将矩形ABCD绕点A逆时针旋转，得到矩形AEFG，点B的对应点E落在CD上，且DE=EF，则AB的长为________.
65°
32
6.如图，四边形ABCD是边长为1的正方形，且DE=14，△ABF是△ADE的旋转图形.
（1）旋转中心是哪一点？
（2）旋转了多少度？
（3）AF的长度是多少？
（4）如果连接EF，那么△AEF是什么三角形？
解 (1)旋转中心是点A.
(2)旋转了90°.
(4)△AEF是等腰直角三角形.
(3)AF= .
7.如图，在△ABC中，∠CAB=70°，将△ABC绕点A逆时针旋转到△AB′C′的位置，使得CC′∥AB，求∠CAB′的度数.
∴∠CAB′=∠C′AB′-∠C′AC=30°.
解 由旋转的性质可知
AC=AC′，∠C′AB′=∠CAB=70°，
∴∠AC′C=∠ACC′.
∵CC′∥AB，
∴∠ACC′=∠CAB=70°，
∴∠C′AC=40°，
课堂小结
旋转的概念及性质

概念
性质


1.对应点到旋转中心的距离相等.
2.对应点与旋转中心所连的线段的夹角等于旋转角.
3.旋转前后的图形全等.
在平面内，把一个图形绕一个定点按某个方向转动一个角度，这样的图形运动称为旋转.这个定点称为旋转中心.转动的角称为旋转角.如果图形上的点P经过旋转变为点P'，这两个点叫做这个旋转的对应点.
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php