23.1 图形的旋转 第2课时 课件

(共24张PPT)
23.1 图形的旋转
第二十三章 旋转




课程讲授





















新知导入







随堂练习




课堂小结
第2课时 旋转的计算与作图
知识要点
1.利用旋转的性质进行证明和计算
2.旋转作图
3.平面直角坐标系里的旋转
新知导入
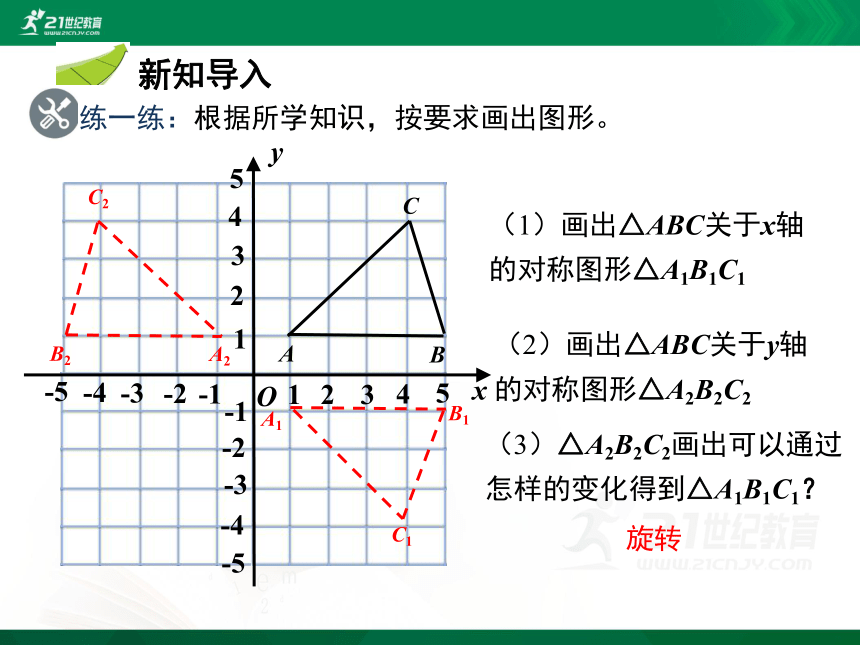
练一练：根据所学知识，按要求画出图形。
（1）画出△ABC关于x轴的对称图形△A1B1C1
-1
-2
-3
-4
5
1
-2
3
-4
-5
-1
2
-3
4
-5
1
2
3
4
5
y
O
x
C
A
B
C1
A1
B1
（2）画出△ABC关于y轴的对称图形△A2B2C2
C2
A2
B2
（3）△A2B2C2画出可以通过怎样的变化得到△A1B1C1？
旋转
课程讲授
1
利用旋转的性质进行证明和计算
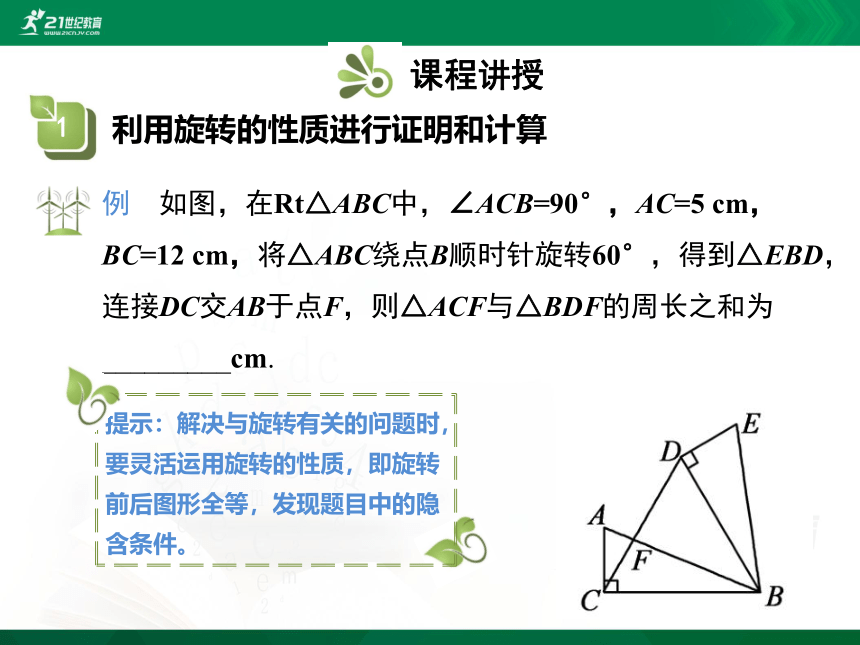
例 如图，在Rt△ABC中，∠ACB=90°，AC=5 cm，BC=12 cm，将△ABC绕点B顺时针旋转60°，得到△EBD，连接DC交AB于点F，则△ACF与△BDF的周长之和为_________cm.
提示：解决与旋转有关的问题时，要灵活运用旋转的性质，即旋转前后图形全等，发现题目中的隐含条件。
1
利用旋转的性质进行证明和计算
解 根据旋转的性质可Rt△ABC≌Rt△EBD.
∵在Rt△ABC中，∠ACB=90°，
AC=5 cm，BC=12 cm，
∴AB=EB=13cm.
∵△ABC绕点B顺时针旋转60°,DB=BC,
∴△DBC为等边三角形.
△ACF与△BDF的周长之和=AC+FA+CF+BD+FB+DF
=AC+DC+AB+BD
=42cm
1
利用旋转的性质进行证明和计算
归纳：利用旋转的性质进行证明和计算时，要寻找题目中隐含的条件，解题时可运用全等实现线段或者数量关系的转化，将问题简化。
1
利用旋转的性质进行证明和计算
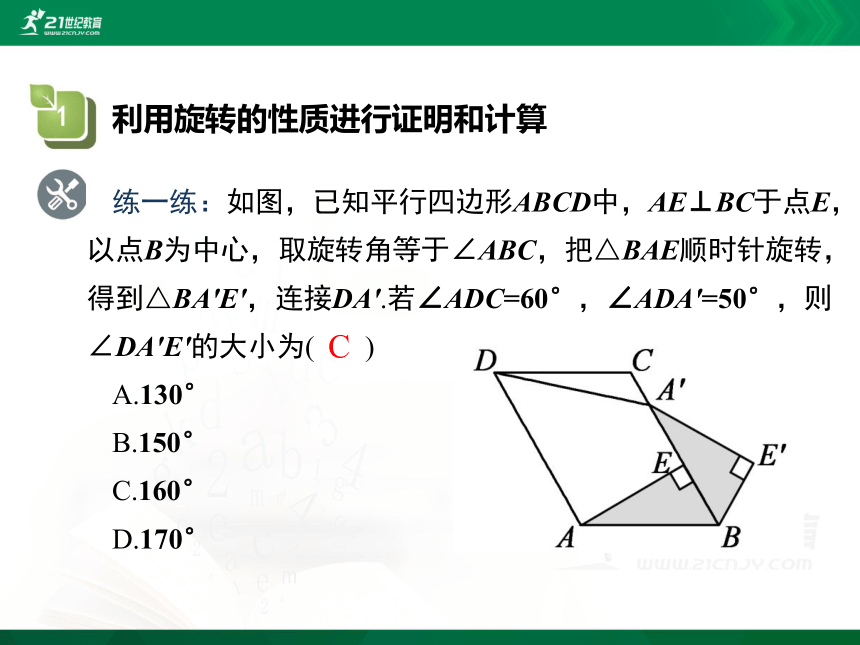
练一练：如图，已知平行四边形ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′.若∠ADC=60°，∠ADA′=50°，则∠DA′E′的大小为( )
A.130°
B.150°
C.160°
D.170°
C
2
旋转作图
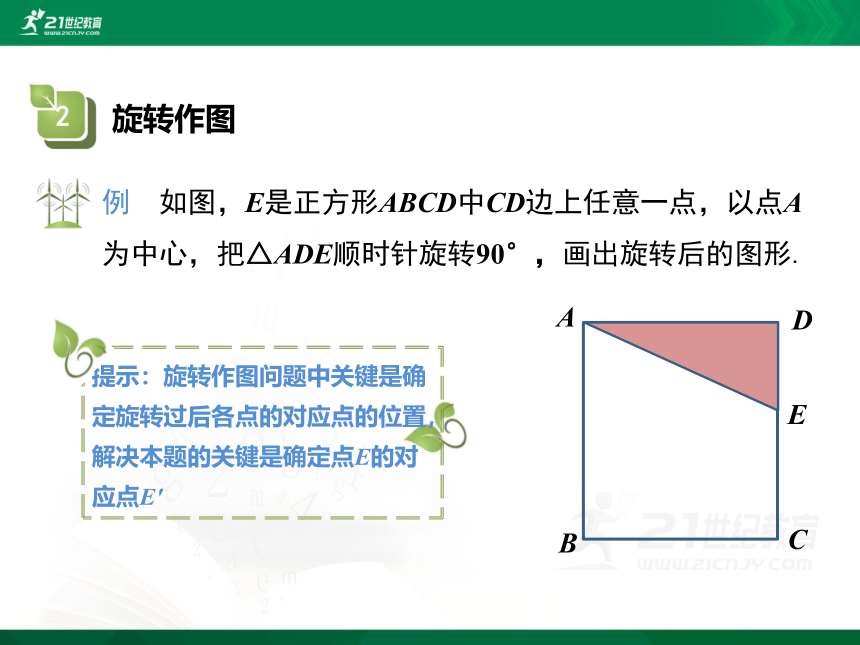
例 如图，E是正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形.


D
A
B
C
E
提示：旋转作图问题中关键是确定旋转过后各点的对应点的位置，解决本题的关键是确定点E的对应点E′
2
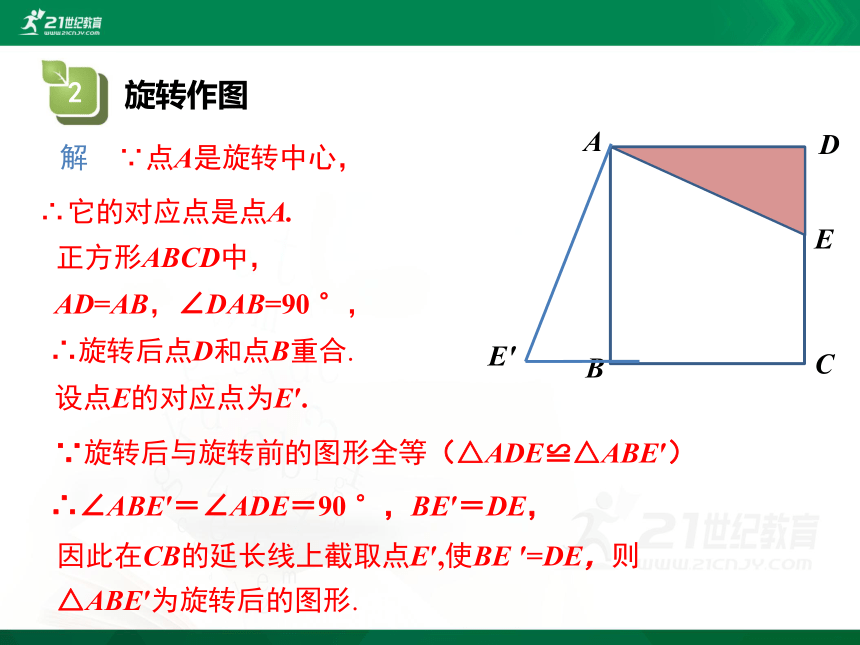
旋转作图
因此在CB的延长线上截取点E′,使BE ′=DE，则△ABE′为旋转后的图形.
解 ∵点A是旋转中心，


D
A
B
C
E
∴它的对应点是点A.
正方形ABCD中，
∴旋转后点D和点B重合.
设点E的对应点为E′.
∵旋转后与旋转前的图形全等（△ADE≌△ABE′）
∴∠ABE′＝∠ADE＝90 °，BE′＝DE，
AD=AB，∠DAB=90 °，
E'
2
旋转作图
旋转作图的一般步骤：
(1)明确旋转三要素：________、________、________；
(2)找出关键点；
(3)作出关键点的________；
(4)作出新图形；
(5)写出结论；
对应点
旋转角度
旋转中心
旋转方向
2
旋转作图
练一练：将△AOB绕点O旋转180°得到△DOE，则下列作图正确的是（ ）
C
3
平面直角坐标系里的旋转
例 如图，将△ABC绕点P顺时针旋转90°得到△A′B′C′，则点P的坐标是（ ）
A.（1，1）
B.（1，2）
C.（1，3）
D.（1，4）

3
平面直角坐标系里的旋转
P
故选B
3
平面直角坐标系里的旋转
归纳：直角坐标系中的旋转问题可以借助各个点的坐标进行解答，不仅能够确定旋转后对应点的坐标，还能根据旋转前后两点对应的关系确定旋转中的旋转中心即旋转角度.
3
平面直角坐标系里的旋转
练一练：如图，若将△ABC绕点O逆时针旋转90°，则顶点B的对应点B1的坐标为（ ）
A.（-4，2）
B.（-2，4）
C.（4，-2）
D.（2，-4）
B
随堂练习
1.如图，在平面直角坐标系中，△ABC的三个顶点均在格点上.
（1）填空：△ABC是_________三角形，
它的面积等于_____平方单位；
（2）将△ACB绕点O顺时针方
向旋转90°，在方格图中画出
旋转后对应的△A′B′C′，则点A′
的坐标是_______，点B′的坐标是
_______，点C′的坐标是_______；
（3）B′C′与BC的位置关系是__________.
B′C′⊥BC
等腰直角
5
（-2，2）
（1，3）
（-1，-1）
A′
C′
B′
2.如图，在△ABC中，AB=4，BC=6，∠B=60°，将△ABC沿射线BC的方向平移，得到△A′B′C′，再将△A′B′C′绕点A′逆时针旋转一定角度后，点B′恰好与点C重合，则平移的距离和旋转角的度数分别为( )
A.4，30°
B.2，60°
C.1，30°
D.3，60°
B
3.如图，正方形OABC的两边OA，OC分别在x轴、y轴上，点D（5，3）在边AB上，以点C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是( )
A.（2，10）
B.（-2，0）
C. （2，10）或(-2,0)
D.(10,2)或(-2,0)
C
4.如图，在边长为1的小正方形组成的方格图中，将△ABC绕着点A顺时针旋转90°，画出旋转后的△AB′C′.
C′
B′
5.如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（1，1），B（4，1），C（3，3）.
（1）将△ABC向下平移5个单位长度后得到△A1B1C1，请画出△A1B1C1；
（2）将△ABC绕原点O逆时
针旋转90°后得到△A2B2C2，
请画出△A2B2C2；
（3）判断以O，A1，B为顶点
的三角形的形状.（无需说明
理由）
（3）等腰直角三角形.
解 （1）如图所示.
（2）如图所示.
C1
A1
B1
C2
A2
B2
课堂小结
旋转的计算与作图

作旋转图形

与旋转有关的证明和计算

灵活运用旋转的性质：旋转前后的图形全等
旋转作图的一般步骤：
(1)明确旋转三要素：旋转中心、旋转方向和旋转角度.；
(2)找出关键点；
(3)作出关键点的对应点；
(4)作出新图形；
(5)写出结论；
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php