24.1.2 垂直于弦的直径 课件
图片预览







文档简介
(共23张PPT)
24.1 圆的有关性质
24.1.2 垂直于弦的直径
第二十四章 圆
课程讲授
新知导入
随堂练习
课堂小结
知识要点
1.垂径定理及其推论
2.垂径定理及推论的应用
新知导入
看一看:观察下图中图形的变化,试着发现它们的规律。
看一看:观察下图中图形的变化,试着发现它们的规律。
课程讲授
1
垂径定理及其推论
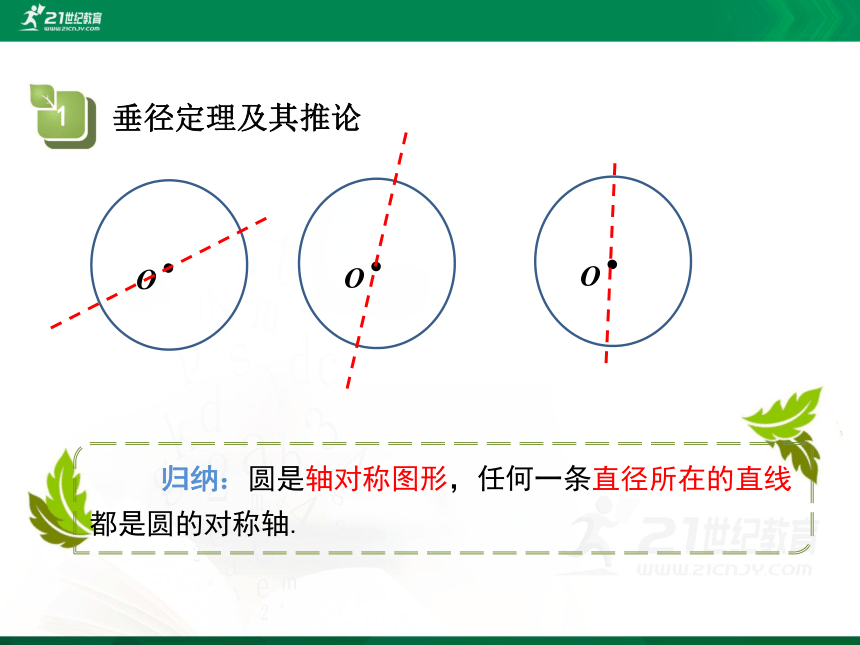
问题1:剪一个圆形纸片,沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得出什么结论?你能证明你的结论吗?
1
垂径定理及其推论
O
O
O
归纳:圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
1
垂径定理及其推论
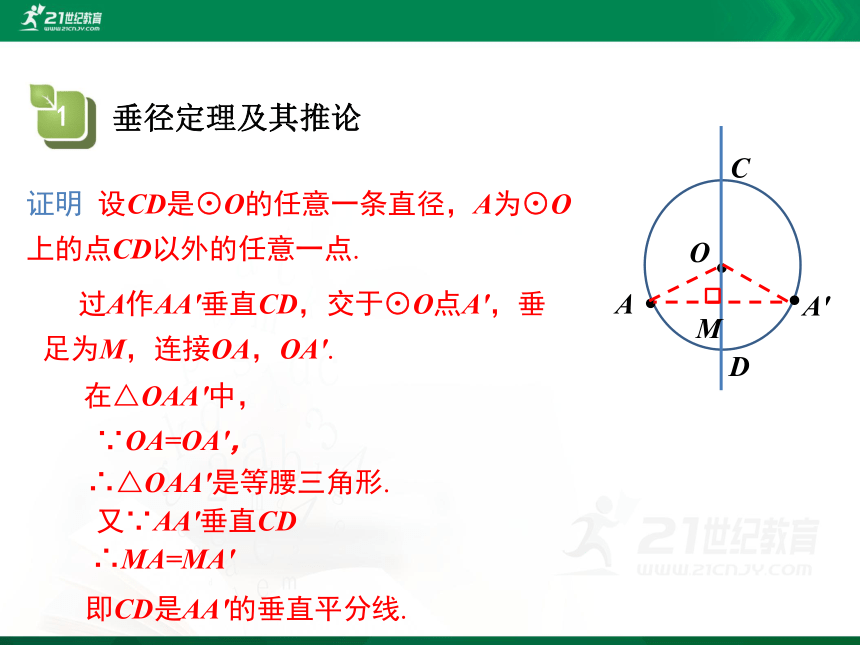
证明 设CD是⊙O的任意一条直径,A为⊙O上的点CD以外的任意一点.
O
A
D
C
过A作AA'垂直CD,交于⊙O点A',垂足为M,连接OA,OA'.
A'
M
在△OAA'中,
∵OA=OA',
∴△OAA'是等腰三角形.
又∵AA'垂直CD
∴MA=MA'
即CD是AA'的垂直平分线.
1
垂径定理及其推论
从上面的证明过程中我们可以知道:
把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点A'重合,AE与BE重合,AC和A'C,AD与A'D重合.
⌒
⌒
⌒
⌒
∴MA=MA',AC=A'C,AD=A'D
)
)
)
)
即直径CD平分弦AA',并且平分AA',ACA'
)
)
1
垂径定理及其推论
垂径定理:
垂直于弦的直径_______,并且平分_______________.
垂径定理的推论:
平分弦(不是直径)的直径_________,并且___________________.
平分弦
弦所对的两条弧
垂直于弦
平分弦所对的弧
1
垂径定理及其推论
练一练:下列命题中,正确的是( )
A.平分弦的直线,必垂直于弧
B.垂直于弦的直线,必经过圆心
C.垂直平分弦的直线必平分弦所对的弧
D.平分弦的直径必垂直于弦并且平分弦所对的两条弧
C
2
垂径定理及推论的应用
例 赵州桥是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代劳动人民勤劳与智慧的结晶。它的主桥拱是圆弧形,它的跨度(弧所对的弦长)为37m,拱高(弧的中点到弦的距离)为7.23m,求赵州桥主桥拱半径(结果保留小数点后一位).
提示:根据顶点的提示,解决此问题的关键是根据赵州桥的实物图画出几何图形.
2
垂径定理及推论的应用
A
B
R
解 如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
C
D
由题设可知AB=37 ,CD=7.23 .
∴ AD= AB=18.5,
OD=OC-CD=R-7.23.
2
1
在Rt△OAD中,由勾股定理,得
OA2=AD2+OD2
即
=18.52+(R-7.23)2
解得R≈27.3(m).
因此,赵州桥主桥拱半径约为27.3m.
2
垂径定理及推论的应用
练一练:如图,小丽荡秋千,秋千链子的长OA为2.5米,秋千向两边摆动的角度相同,摆动的水平距离AB为3米,则秋千摆至最高位置时与其摆至最低位置时的高度之差(即CD)为_______米.
0.5
随堂练习
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5 cm,CD=8 cm,则AE=( )
A.8 cm
B.9 cm
C.7 cm
D.6 cm
A
2.如图,⊙O的弦AB=8,半径ON交AB于点M,M是AB的中点,且OM=3,则MN的长为( )
A.2
B.3
C.4
D.5
A
3.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译文:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸),问这块圆柱形木材的直径是多少?如图,请根据所学的知识计算:圆柱形木材的直径AC是( )
A.13寸 B.20寸
C.26寸 D.28寸
C
4.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为13,则点P的坐标为________.
(3,2)
5.如图,⊙O的直径为10,弦AB长为8,点P在AB上运动,则OP的最小值是________.
3
6.如图,直径AB垂直于弦CD于点E,CD=4,AE=8,⊙O的半径长为________.
4
17
7.如图,有一个拱桥是圆弧形,它的跨度为60 m,拱高为18 m,求拱桥的半径.
解得x=34.
解 设圆弧的圆心为点O,过点O作OD⊥AB,交AB于点D,交圆弧于点E,
O
E
D
则AD=BD= AB=30 m,
2
1
DE=18 m.
设拱桥的半径为x m,
则(x-18)2+302=x2,
即拱桥的半径为34 m.
课堂小结
垂直于弦的直径
垂弦定理
的推论
垂弦定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
24.1 圆的有关性质
24.1.2 垂直于弦的直径
第二十四章 圆
课程讲授
新知导入
随堂练习
课堂小结
知识要点
1.垂径定理及其推论
2.垂径定理及推论的应用
新知导入
看一看:观察下图中图形的变化,试着发现它们的规律。
看一看:观察下图中图形的变化,试着发现它们的规律。
课程讲授
1
垂径定理及其推论
问题1:剪一个圆形纸片,沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得出什么结论?你能证明你的结论吗?
1
垂径定理及其推论
O
O
O
归纳:圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
1
垂径定理及其推论
证明 设CD是⊙O的任意一条直径,A为⊙O上的点CD以外的任意一点.
O
A
D
C
过A作AA'垂直CD,交于⊙O点A',垂足为M,连接OA,OA'.
A'
M
在△OAA'中,
∵OA=OA',
∴△OAA'是等腰三角形.
又∵AA'垂直CD
∴MA=MA'
即CD是AA'的垂直平分线.
1
垂径定理及其推论
从上面的证明过程中我们可以知道:
把圆沿着直径CD折叠时,CD两侧的两个半圆重合,点A与点A'重合,AE与BE重合,AC和A'C,AD与A'D重合.
⌒
⌒
⌒
⌒
∴MA=MA',AC=A'C,AD=A'D
)
)
)
)
即直径CD平分弦AA',并且平分AA',ACA'
)
)
1
垂径定理及其推论
垂径定理:
垂直于弦的直径_______,并且平分_______________.
垂径定理的推论:
平分弦(不是直径)的直径_________,并且___________________.
平分弦
弦所对的两条弧
垂直于弦
平分弦所对的弧
1
垂径定理及其推论
练一练:下列命题中,正确的是( )
A.平分弦的直线,必垂直于弧
B.垂直于弦的直线,必经过圆心
C.垂直平分弦的直线必平分弦所对的弧
D.平分弦的直径必垂直于弦并且平分弦所对的两条弧
C
2
垂径定理及推论的应用
例 赵州桥是我国隋代建造的石拱桥,距今约有1400年的历史,是我国古代劳动人民勤劳与智慧的结晶。它的主桥拱是圆弧形,它的跨度(弧所对的弦长)为37m,拱高(弧的中点到弦的距离)为7.23m,求赵州桥主桥拱半径(结果保留小数点后一位).
提示:根据顶点的提示,解决此问题的关键是根据赵州桥的实物图画出几何图形.
2
垂径定理及推论的应用
A
B
R
解 如图,用AB表示主桥拱,设AB所在圆的圆心为O,半径为R.
经过圆心O作弦AB的垂线OC垂足为D,与弧AB交于点C,则D是AB的中点,C是弧AB的中点,CD就是拱高.
C
D
由题设可知AB=37 ,CD=7.23 .
∴ AD= AB=18.5,
OD=OC-CD=R-7.23.
2
1
在Rt△OAD中,由勾股定理,得
OA2=AD2+OD2
即
=18.52+(R-7.23)2
解得R≈27.3(m).
因此,赵州桥主桥拱半径约为27.3m.
2
垂径定理及推论的应用
练一练:如图,小丽荡秋千,秋千链子的长OA为2.5米,秋千向两边摆动的角度相同,摆动的水平距离AB为3米,则秋千摆至最高位置时与其摆至最低位置时的高度之差(即CD)为_______米.
0.5
随堂练习
1.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5 cm,CD=8 cm,则AE=( )
A.8 cm
B.9 cm
C.7 cm
D.6 cm
A
2.如图,⊙O的弦AB=8,半径ON交AB于点M,M是AB的中点,且OM=3,则MN的长为( )
A.2
B.3
C.4
D.5
A
3.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译文:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸),问这块圆柱形木材的直径是多少?如图,请根据所学的知识计算:圆柱形木材的直径AC是( )
A.13寸 B.20寸
C.26寸 D.28寸
C
4.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为13,则点P的坐标为________.
(3,2)
5.如图,⊙O的直径为10,弦AB长为8,点P在AB上运动,则OP的最小值是________.
3
6.如图,直径AB垂直于弦CD于点E,CD=4,AE=8,⊙O的半径长为________.
4
17
7.如图,有一个拱桥是圆弧形,它的跨度为60 m,拱高为18 m,求拱桥的半径.
解得x=34.
解 设圆弧的圆心为点O,过点O作OD⊥AB,交AB于点D,交圆弧于点E,
O
E
D
则AD=BD= AB=30 m,
2
1
DE=18 m.
设拱桥的半径为x m,
则(x-18)2+302=x2,
即拱桥的半径为34 m.
课堂小结
垂直于弦的直径
垂弦定理
的推论
垂弦定理
垂直于弦的直径平分弦,并且平分弦所对的两条弧.
平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
