24.1.3 弧、弦、圆心角 课件
图片预览





文档简介
(共24张PPT)
24.1 圆的有关性质
24.1.3 弧、弦、圆心角
第二十四章 圆
课程讲授
新知导入
随堂练习
课堂小结
知识要点
1.圆心角
2.弧、弦、圆心角之间的关系
新知导入
看一看:观察下图中图形的变化,试着发现它们的规律。
看一看:观察下图中图形的变化,试着发现它们的规律。
1
圆心角
问题1:剪下一个圆形纸片,把它绕圆心旋转180°,所得的图形与原图形重合吗?由此你得到什么结论?把圆绕圆心旋转任意一个角度呢?
B
A
圆是中心对称图形,圆心就是它的对称中心.
1
圆心角
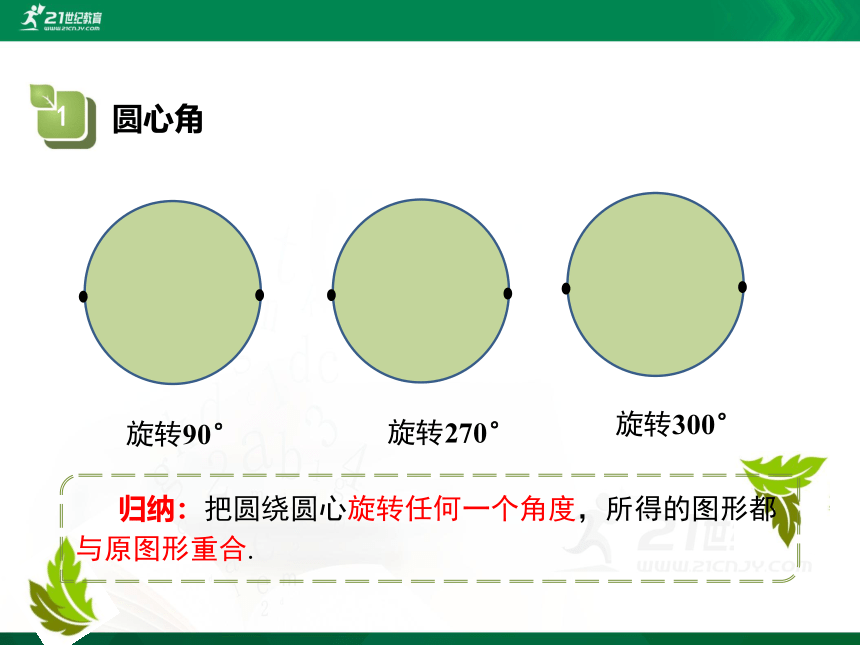
旋转90°
旋转270°
旋转300°
归纳:把圆绕圆心旋转任何一个角度,所得的图形都与原图形重合.
1
圆心角
O
r
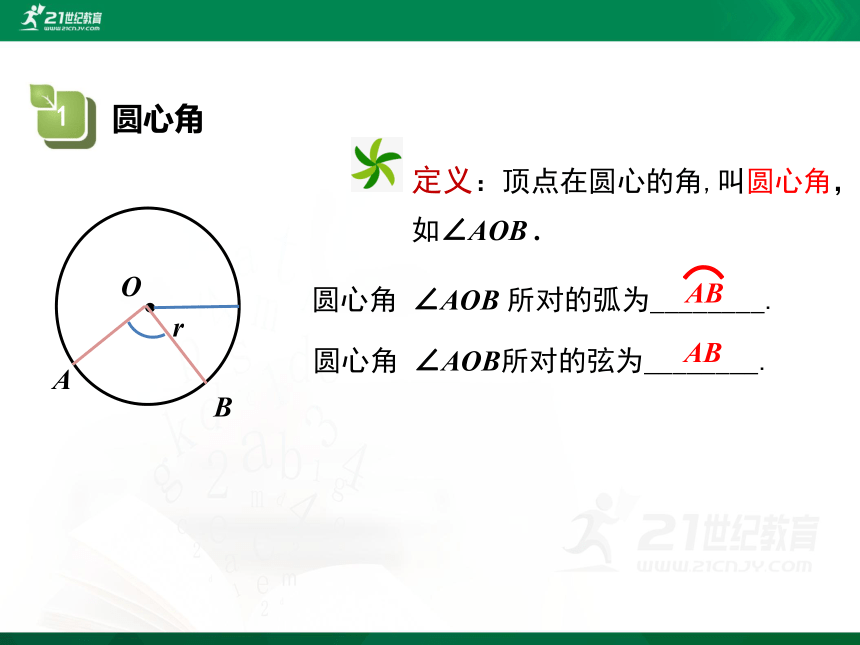
定义:顶点在圆心的角,叫圆心角,如∠AOB .
B
A
圆心角 ∠AOB 所对的弧为________.
圆心角 ∠AOB所对的弦为________.
AB
AB
)
1
圆心角
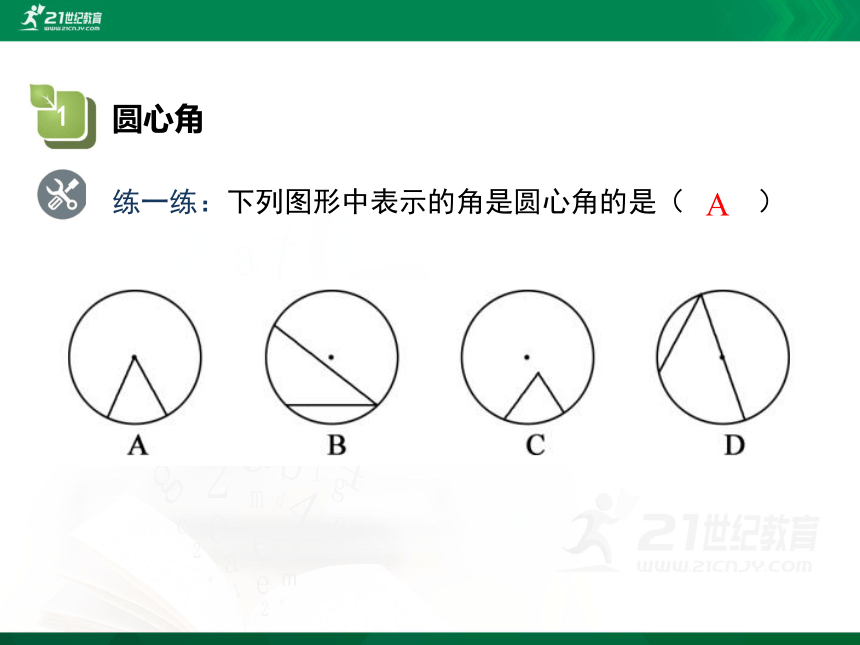
练一练:下列图形中表示的角是圆心角的是( )
A
2
弧、弦、圆心角之间的关系
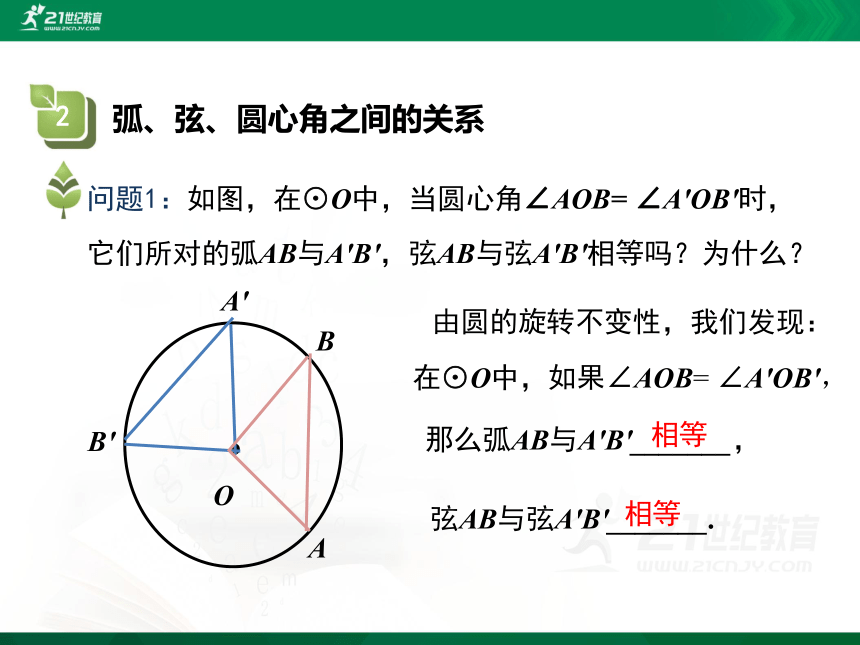
问题1:如图,在⊙O中,当圆心角∠AOB= ∠A'OB'时,它们所对的弧AB与A'B',弦AB与弦A'B'相等吗?为什么?
O
B'
A
B
A'
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠A'OB',
那么弧AB与A'B'_______,
弦AB与弦A'B'_______.
相等
相等
2
弧、弦、圆心角之间的关系
我们把∠AOB连同AB绕圆心O旋转,使射线OA与OA'重合.
O
B'
A
B
A'
∵∠AOB= ∠A'OB'
∴射线OB与OB'重合
∵OA=OA',OB=OB'
∴点A与A'重合,点B与B'重合
因此点AB与A'B'重合,AB与A'B'重合
)
)
∴AB=A'B'
.
)
)
AB=A'B'
2
弧、弦、圆心角之间的关系
归纳:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
O
r
O
r
2
弧、弦、圆心角之间的关系
弧、弦、圆心角之间的关系:
1.在同圆或等圆中,如果两条弧相等,那么它们所对应的圆心角______,所对的弦______.
2.在同圆或等圆中,如果两条弦相等,那么它们所对应的圆心角______,所对的优弧和劣弧分别_____.
相等
相等
相等
相等
2
弧、弦、圆心角之间的关系
例 如图,在⊙O中, AB=AC ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
)
)
C
A
B
O
证明 ∵AB=AC
)
)
∴ AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴ △ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
2
弧、弦、圆心角之间的关系
练一练:在同圆中,下列四个命题:
①圆心角是顶点在圆心的角;
②两个圆心角相等,它们所对的弦也相等;
③两条弦相等,它们所对的弧也相等;
④等弧所对的圆心角相等.其中真命题有( )
A.①②③④ B.①②④
C.②③④ D.②④
B
随堂练习
A
1.如图,AB是⊙O的直径,点D是⊙O上一点,且∠AOD=100°,若点C为BD的中点,则∠COB的度数为( )
A.40°
B.60°
C.80°
D.120°
2.如图,A,B,C,D是⊙O上的四点,且AD=BC,则AB与CD的大小关系为( )
A.AB>CD
B.AB=CD
C.AB<CD
D.不能确定
B
D
3.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有( )
①AB=CD;
②BD=AC;
③AC=BD;
④∠BOD=∠AOC.
A.1个 B.2个
C.3个 D.4个
)
)
)
)
4.如图,已知⊙O的半径OA=5 cm,弦CD=5 cm,则弦CD所对的圆心角的度数为_________.
60°
5.如图,D,E分别是⊙O的半径OA,OB上的点,CD⊥OA,CE⊥OB,CD=CE,则AC与BC的大小关系是________.
AC=BC
6.如图,点O为半圆的圆心,C,D为半圆上的三等分点,AB为直径,则下列说法:
①AD=CD=BC;
②∠AOD=∠DOC=∠BOC;
③AD=CD=BC;
④△AOD沿OD翻折能与△COD重合.
其中正确的有___________.(填序号)
)
)
)
①②③④
7.如图,AB为⊙O的弦,点C,D为弦AB上的两点,且OC=OD,延长OC,OD分别交⊙O于点E,F.
求证:AE=BF.
)
)
即∠AOE=∠BOF,
证明 ∵OC=OD,
∴∠OCD=∠ODC.
又∵OA=OB,
∴∠OAC=∠OBD,
∴∠OCD-∠OAC=∠ODC-∠OBD,
∴∠AOC=∠BOD,
∴AE=BF.
)
)
∴AC∥OD.
8.如图,AB是⊙O的直径,若BD=CD.求证:AC∥OD.
)
)
证明 连接OC.
∴∠BOD=∠COD.
∵OA=OC,
∵BD=CD,
)
)
∴∠A=∠C.
∵∠COB=∠A+∠C=∠COD+∠BOD,
∴∠A=∠C=∠COD=∠BOD,
课堂小结
弧、弦、圆心角
弧、弦、圆心角之间的关系
圆心角
顶点在圆心的角,叫圆心角.
在同圆或等圆中,如果两条弦相等,那么它们所对应的圆心角相等,所对的优弧和劣弧分别相等.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
在同圆或等圆中,如果两条弧相等,那么它们所对应的圆心角相等,所对的弦相等.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
24.1 圆的有关性质
24.1.3 弧、弦、圆心角
第二十四章 圆
课程讲授
新知导入
随堂练习
课堂小结
知识要点
1.圆心角
2.弧、弦、圆心角之间的关系
新知导入
看一看:观察下图中图形的变化,试着发现它们的规律。
看一看:观察下图中图形的变化,试着发现它们的规律。
1
圆心角
问题1:剪下一个圆形纸片,把它绕圆心旋转180°,所得的图形与原图形重合吗?由此你得到什么结论?把圆绕圆心旋转任意一个角度呢?
B
A
圆是中心对称图形,圆心就是它的对称中心.
1
圆心角
旋转90°
旋转270°
旋转300°
归纳:把圆绕圆心旋转任何一个角度,所得的图形都与原图形重合.
1
圆心角
O
r
定义:顶点在圆心的角,叫圆心角,如∠AOB .
B
A
圆心角 ∠AOB 所对的弧为________.
圆心角 ∠AOB所对的弦为________.
AB
AB
)
1
圆心角
练一练:下列图形中表示的角是圆心角的是( )
A
2
弧、弦、圆心角之间的关系
问题1:如图,在⊙O中,当圆心角∠AOB= ∠A'OB'时,它们所对的弧AB与A'B',弦AB与弦A'B'相等吗?为什么?
O
B'
A
B
A'
由圆的旋转不变性,我们发现:
在⊙O中,如果∠AOB= ∠A'OB',
那么弧AB与A'B'_______,
弦AB与弦A'B'_______.
相等
相等
2
弧、弦、圆心角之间的关系
我们把∠AOB连同AB绕圆心O旋转,使射线OA与OA'重合.
O
B'
A
B
A'
∵∠AOB= ∠A'OB'
∴射线OB与OB'重合
∵OA=OA',OB=OB'
∴点A与A'重合,点B与B'重合
因此点AB与A'B'重合,AB与A'B'重合
)
)
∴AB=A'B'
.
)
)
AB=A'B'
2
弧、弦、圆心角之间的关系
归纳:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
O
r
O
r
2
弧、弦、圆心角之间的关系
弧、弦、圆心角之间的关系:
1.在同圆或等圆中,如果两条弧相等,那么它们所对应的圆心角______,所对的弦______.
2.在同圆或等圆中,如果两条弦相等,那么它们所对应的圆心角______,所对的优弧和劣弧分别_____.
相等
相等
相等
相等
2
弧、弦、圆心角之间的关系
例 如图,在⊙O中, AB=AC ,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
)
)
C
A
B
O
证明 ∵AB=AC
)
)
∴ AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴ △ABC是等边三角形 , AB=BC=CA.
∴ ∠AOB=∠BOC=∠AOC.
2
弧、弦、圆心角之间的关系
练一练:在同圆中,下列四个命题:
①圆心角是顶点在圆心的角;
②两个圆心角相等,它们所对的弦也相等;
③两条弦相等,它们所对的弧也相等;
④等弧所对的圆心角相等.其中真命题有( )
A.①②③④ B.①②④
C.②③④ D.②④
B
随堂练习
A
1.如图,AB是⊙O的直径,点D是⊙O上一点,且∠AOD=100°,若点C为BD的中点,则∠COB的度数为( )
A.40°
B.60°
C.80°
D.120°
2.如图,A,B,C,D是⊙O上的四点,且AD=BC,则AB与CD的大小关系为( )
A.AB>CD
B.AB=CD
C.AB<CD
D.不能确定
B
D
3.如图,已知A,B,C,D是⊙O上的点,∠1=∠2,则下列结论中正确的有( )
①AB=CD;
②BD=AC;
③AC=BD;
④∠BOD=∠AOC.
A.1个 B.2个
C.3个 D.4个
)
)
)
)
4.如图,已知⊙O的半径OA=5 cm,弦CD=5 cm,则弦CD所对的圆心角的度数为_________.
60°
5.如图,D,E分别是⊙O的半径OA,OB上的点,CD⊥OA,CE⊥OB,CD=CE,则AC与BC的大小关系是________.
AC=BC
6.如图,点O为半圆的圆心,C,D为半圆上的三等分点,AB为直径,则下列说法:
①AD=CD=BC;
②∠AOD=∠DOC=∠BOC;
③AD=CD=BC;
④△AOD沿OD翻折能与△COD重合.
其中正确的有___________.(填序号)
)
)
)
①②③④
7.如图,AB为⊙O的弦,点C,D为弦AB上的两点,且OC=OD,延长OC,OD分别交⊙O于点E,F.
求证:AE=BF.
)
)
即∠AOE=∠BOF,
证明 ∵OC=OD,
∴∠OCD=∠ODC.
又∵OA=OB,
∴∠OAC=∠OBD,
∴∠OCD-∠OAC=∠ODC-∠OBD,
∴∠AOC=∠BOD,
∴AE=BF.
)
)
∴AC∥OD.
8.如图,AB是⊙O的直径,若BD=CD.求证:AC∥OD.
)
)
证明 连接OC.
∴∠BOD=∠COD.
∵OA=OC,
∵BD=CD,
)
)
∴∠A=∠C.
∵∠COB=∠A+∠C=∠COD+∠BOD,
∴∠A=∠C=∠COD=∠BOD,
课堂小结
弧、弦、圆心角
弧、弦、圆心角之间的关系
圆心角
顶点在圆心的角,叫圆心角.
在同圆或等圆中,如果两条弦相等,那么它们所对应的圆心角相等,所对的优弧和劣弧分别相等.
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
在同圆或等圆中,如果两条弧相等,那么它们所对应的圆心角相等,所对的弦相等.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
