24.2.1 点和圆的位置关系 课件
图片预览






文档简介
(共29张PPT)
24.2 点和圆、直线和圆的
位置关系
24.2.1 点和圆的位置关系
课程讲授
新知导入
随堂练习
课堂小结
第二十四章 圆
知识要点
1.点和圆的位置关系
2.三角形的外接圆与外心
3.反证法
新知导入
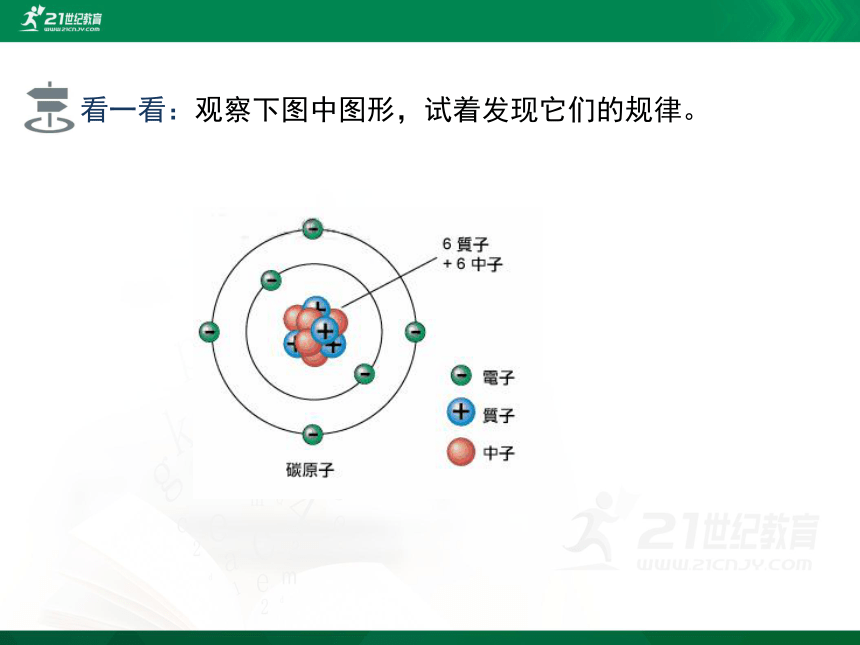
看一看:观察下图中图形,试着发现它们的规律。
看一看:观察下图中图形,试着发现它们的规律。
课程讲授
1
点和圆的位置关系
问题1:杜丽是我国著名的射击运动员,屡次获得奥运奖牌,为祖国赢得荣誉.下图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不等的圆)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
1
点和圆的位置关系
击中靶上不同位置的成绩是根据距离靶心的距离决定的,距离靶心越近,得分越高.
要进一步解决这个问题,我们需要研究点和圆的位置关系.
1
点和圆的位置关系
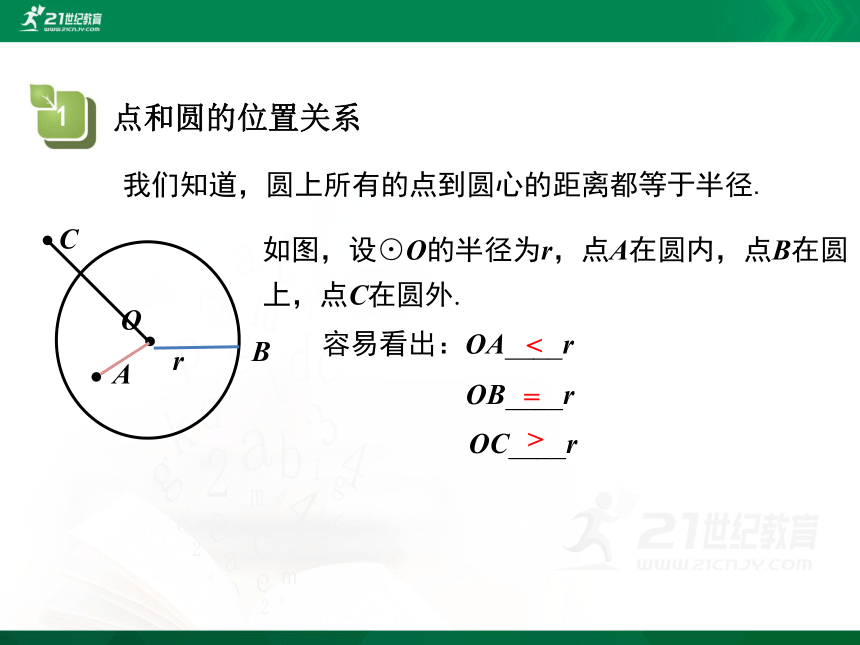
我们知道,圆上所有的点到圆心的距离都等于半径.
B
O
r
如图,设⊙O的半径为r,点A在圆内,点B在圆上,点C在圆外.
C
A
容易看出:OA____r
OB____r
OC____r
>
<
=
1
点和圆的位置关系
反过来说:如果OAOB=r,点B在圆____
OC>r,点C在圆_____
B
O
r
C
A
内
上
外
1
点和圆的位置关系
点和圆的位置关系:
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
(1)点P在⊙O内 _________
(2)点P在⊙O上 _________
(3)点P在⊙O外 _________
d>r
d=r
d1
点和圆的位置关系
练一练:已知⊙O的直径为6 cm,点A不在⊙O内,则OA的长( )
A.大于3 cm
B.不小于3 cm
C.大于6 cm
D.不小于6 cm
B
2
三角形的外接圆与外心
问题1.1:如何过一个点A作一个圆?过点A可以作多少个圆?
A
过点A可以作无数个圆
2
三角形的外接圆与外心
问题1.2:如何过已知的两点A,B作一个圆?过点A,B可以作多少个圆?
A
B
圆心在线段AB的垂直平分线上,这样的圆可作出无数个
2
三角形的外接圆与外心
问题1.3:经过不在同一直线上的三点A、B、C能不能作圆?如果能,如何确定所作圆的圆心?
A
B
C
因为所求的圆要经过三点A、B、C,所以圆心到这个三点的距离要相等
圆心在线段_____、______、_____ 的垂直平分线上,
BC
AB
CA
即圆心为这三条线段垂直平分线的____
交点
2
三角形的外接圆与外心
A
B
C
O
归纳:不在同一直线上的三个点确定一个 圆.
2
三角形的外接圆与外心
A
B
C
O
定义:经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆.
三角形外接圆的圆心叫做三角形的外心,
它是三角形三条边垂直平分线的交点..
2
三角形的外接圆与外心
练一练:下列说法正确的是( )
A.三点确定一个圆
B.三角形的外心到三角形三边的距离相等
C.三角形有且只有一个外接圆
D.圆有且只有一个内接三角形
C
3
反证法
问题1:经过同一条直线上的三个点能作出一个圆吗?
A
B
C
l1
l2
这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
假设过同一条直线l上三点A、B、C可以作一个圆,
设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,
P
即点P为l1与l2的交点,而l1⊥l,l2⊥l
l
3
反证法
定义:先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
想一想:
你能归纳出反证法的一般解题步骤吗?
3
反证法
反证法的一般解题步骤:
(1)假设命题的结论不成立;
(2)从这个假设出发,经过推理,得出矛盾;
(3)由矛盾判定假设不正确,从而肯定命题的结论正确.
3
反证法
练一练:用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是( )
A.点在圆内
B.点在圆上
C.点在圆心上
D.点在圆上或圆内
D
随堂练习
1.已知⊙A的半径为5,圆心A的坐标为(1,0),点P的坐标为(-2,4),则点P与⊙A的位置关系是( )
A.点P在⊙A上
B.点P在⊙A内
C.点P在⊙A外
D.不能确定
A
2.小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A.2 cm
B.4 cm
C.6 cm
D.8 cm
B
3.已知⊙O的半径是3 cm,若OP=2 cm,则点P在⊙O的_____ ;若点P在⊙O上,则OP=_____cm;若点P在⊙O外,则OP长的取值范围是_________.
4.直角三角形的两边长分别是3和4,则它的外接圆周长是_________.
OP>3 cm
内部
3
4π或5π
5.在同一平面内一点P到⊙O上的点的最大距离为a,最小距离为b(a>b),则此圆的半径为________.
6.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为__________.
或
a+b
2
a-b
2
(-1,-2)
7.如图,在△ABC中,∠ACB=90°,AB=10,BC=8,CD⊥AB于点D,O为AB的中点.
(1)以点C为圆心,6为半径作圆C,试判断点A,D,B与⊙C的位置关系;
(2)⊙C的半径为多少时,点O在⊙C上?
∴⊙C的半径为5时,点O在⊙C上.
解 在△ABC中,
∠ACB=90°,
AB=10,BC=8,CD⊥AB,
由勾股定理得
AC=6,
由三角形面积公式得
S△ABC= AC·BC= AB·CD,
2
1
2
1
∴CD=4.8.
(1)∵AC=6,
∴点A在⊙C上.
∵BC=8>6,
∴点B在⊙C外.
∵CD=4.8<6,
∴点D在⊙C内.
(2)∵点O为AB的中点,
∠ACB=90°,
2
1
∴OC= AB=5,
课堂小结
点和圆的位置关系
三角形的外接圆与外心
点和圆的位置关系
反证法
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
(1)点P在⊙O内,d(2)点P在⊙O上,d=r
(3)点P在⊙O外,d>r
(1)假设命题的结论不成立;
(2)从这个假设出发,经过推理,得出矛盾;
(3)由矛盾判定假设不正确,从而肯定命题的结论正确.
三角形外接圆的圆心叫做三角形的外心,三角形的外接圆的圆心是三边垂直平分线的交点
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
24.2 点和圆、直线和圆的
位置关系
24.2.1 点和圆的位置关系
课程讲授
新知导入
随堂练习
课堂小结
第二十四章 圆
知识要点
1.点和圆的位置关系
2.三角形的外接圆与外心
3.反证法
新知导入
看一看:观察下图中图形,试着发现它们的规律。
看一看:观察下图中图形,试着发现它们的规律。
课程讲授
1
点和圆的位置关系
问题1:杜丽是我国著名的射击运动员,屡次获得奥运奖牌,为祖国赢得荣誉.下图是射击靶的示意图,它是由许多同心圆(圆心相同,半径不等的圆)构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
1
点和圆的位置关系
击中靶上不同位置的成绩是根据距离靶心的距离决定的,距离靶心越近,得分越高.
要进一步解决这个问题,我们需要研究点和圆的位置关系.
1
点和圆的位置关系
我们知道,圆上所有的点到圆心的距离都等于半径.
B
O
r
如图,设⊙O的半径为r,点A在圆内,点B在圆上,点C在圆外.
C
A
容易看出:OA____r
OB____r
OC____r
>
<
=
1
点和圆的位置关系
反过来说:如果OA
OC>r,点C在圆_____
B
O
r
C
A
内
上
外
1
点和圆的位置关系
点和圆的位置关系:
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
(1)点P在⊙O内 _________
(2)点P在⊙O上 _________
(3)点P在⊙O外 _________
d>r
d=r
d
点和圆的位置关系
练一练:已知⊙O的直径为6 cm,点A不在⊙O内,则OA的长( )
A.大于3 cm
B.不小于3 cm
C.大于6 cm
D.不小于6 cm
B
2
三角形的外接圆与外心
问题1.1:如何过一个点A作一个圆?过点A可以作多少个圆?
A
过点A可以作无数个圆
2
三角形的外接圆与外心
问题1.2:如何过已知的两点A,B作一个圆?过点A,B可以作多少个圆?
A
B
圆心在线段AB的垂直平分线上,这样的圆可作出无数个
2
三角形的外接圆与外心
问题1.3:经过不在同一直线上的三点A、B、C能不能作圆?如果能,如何确定所作圆的圆心?
A
B
C
因为所求的圆要经过三点A、B、C,所以圆心到这个三点的距离要相等
圆心在线段_____、______、_____ 的垂直平分线上,
BC
AB
CA
即圆心为这三条线段垂直平分线的____
交点
2
三角形的外接圆与外心
A
B
C
O
归纳:不在同一直线上的三个点确定一个 圆.
2
三角形的外接圆与外心
A
B
C
O
定义:经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆.
三角形外接圆的圆心叫做三角形的外心,
它是三角形三条边垂直平分线的交点..
2
三角形的外接圆与外心
练一练:下列说法正确的是( )
A.三点确定一个圆
B.三角形的外心到三角形三边的距离相等
C.三角形有且只有一个外接圆
D.圆有且只有一个内接三角形
C
3
反证法
问题1:经过同一条直线上的三个点能作出一个圆吗?
A
B
C
l1
l2
这与我们以前学过的“过一点有且只有一条直线与已知直线垂直”相矛盾,所以过同一条直线上的三点不能作圆.
假设过同一条直线l上三点A、B、C可以作一个圆,
设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1上,又在线段BC的垂直平分线l2上,
P
即点P为l1与l2的交点,而l1⊥l,l2⊥l
l
3
反证法
定义:先假设命题的结论不成立,然后由此经过推理得出矛盾(常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
想一想:
你能归纳出反证法的一般解题步骤吗?
3
反证法
反证法的一般解题步骤:
(1)假设命题的结论不成立;
(2)从这个假设出发,经过推理,得出矛盾;
(3)由矛盾判定假设不正确,从而肯定命题的结论正确.
3
反证法
练一练:用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是( )
A.点在圆内
B.点在圆上
C.点在圆心上
D.点在圆上或圆内
D
随堂练习
1.已知⊙A的半径为5,圆心A的坐标为(1,0),点P的坐标为(-2,4),则点P与⊙A的位置关系是( )
A.点P在⊙A上
B.点P在⊙A内
C.点P在⊙A外
D.不能确定
A
2.小颖同学在手工制作中,把一个边长为12 cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
A.2 cm
B.4 cm
C.6 cm
D.8 cm
B
3.已知⊙O的半径是3 cm,若OP=2 cm,则点P在⊙O的_____ ;若点P在⊙O上,则OP=_____cm;若点P在⊙O外,则OP长的取值范围是_________.
4.直角三角形的两边长分别是3和4,则它的外接圆周长是_________.
OP>3 cm
内部
3
4π或5π
5.在同一平面内一点P到⊙O上的点的最大距离为a,最小距离为b(a>b),则此圆的半径为________.
6.如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为__________.
或
a+b
2
a-b
2
(-1,-2)
7.如图,在△ABC中,∠ACB=90°,AB=10,BC=8,CD⊥AB于点D,O为AB的中点.
(1)以点C为圆心,6为半径作圆C,试判断点A,D,B与⊙C的位置关系;
(2)⊙C的半径为多少时,点O在⊙C上?
∴⊙C的半径为5时,点O在⊙C上.
解 在△ABC中,
∠ACB=90°,
AB=10,BC=8,CD⊥AB,
由勾股定理得
AC=6,
由三角形面积公式得
S△ABC= AC·BC= AB·CD,
2
1
2
1
∴CD=4.8.
(1)∵AC=6,
∴点A在⊙C上.
∵BC=8>6,
∴点B在⊙C外.
∵CD=4.8<6,
∴点D在⊙C内.
(2)∵点O为AB的中点,
∠ACB=90°,
2
1
∴OC= AB=5,
课堂小结
点和圆的位置关系
三角形的外接圆与外心
点和圆的位置关系
反证法
设⊙O的半径为r,点P到圆心的距离OP=d,则有:
(1)点P在⊙O内,d
(3)点P在⊙O外,d>r
(1)假设命题的结论不成立;
(2)从这个假设出发,经过推理,得出矛盾;
(3)由矛盾判定假设不正确,从而肯定命题的结论正确.
三角形外接圆的圆心叫做三角形的外心,三角形的外接圆的圆心是三边垂直平分线的交点
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
