24.3 正多边形和圆 课件
图片预览




文档简介
(共19张PPT)
24.3 正多边形和圆
课程讲授
新知导入
随堂练习
课堂小结
第二十四章 圆
知识要点
1.正多边形的有关概念
2.正多边形和圆的有关计算
新知导入
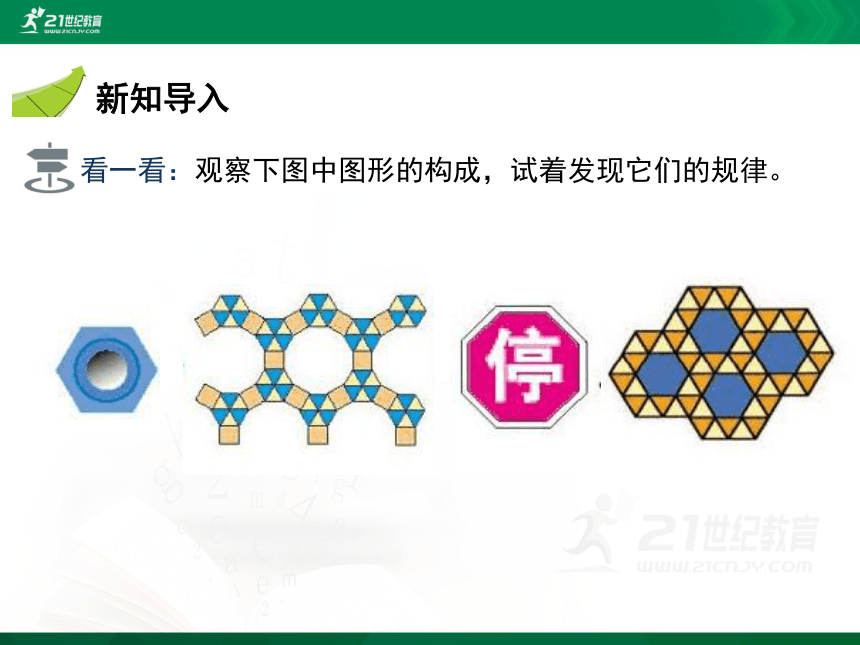
看一看:观察下图中图形的构成,试着发现它们的规律。
课程讲授
1
正多边形的有关概念
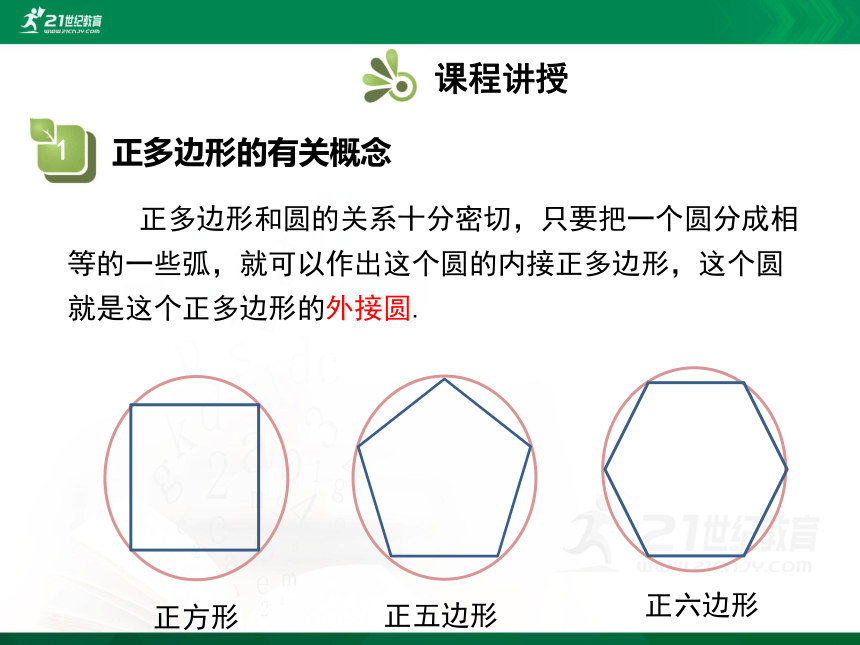
正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
正六边形
正方形
正五边形
1
正多边形的有关概念
以圆的内接正五边形为例证明.
E
A
B
C
D
正五边形
O
如图,把⊙O分成相等的5段弧,依次连接各分点得到五边形ABCDE.
∴AB=BC=CD=DE=EA
∴∠A=∠B
∵∠B=∠C=∠D=∠E
又 五边形ABCDE的顶点都在上,
∵AB=BC=CD=DE=EA
)
)
)
)
)
BCE=3AB=CDA
)
)
)
∴五边形ABCDE是⊙O的内接五边形,
⊙O是五边形ABCDE的外接圆.
1
正多边形的有关概念
正五边形
O
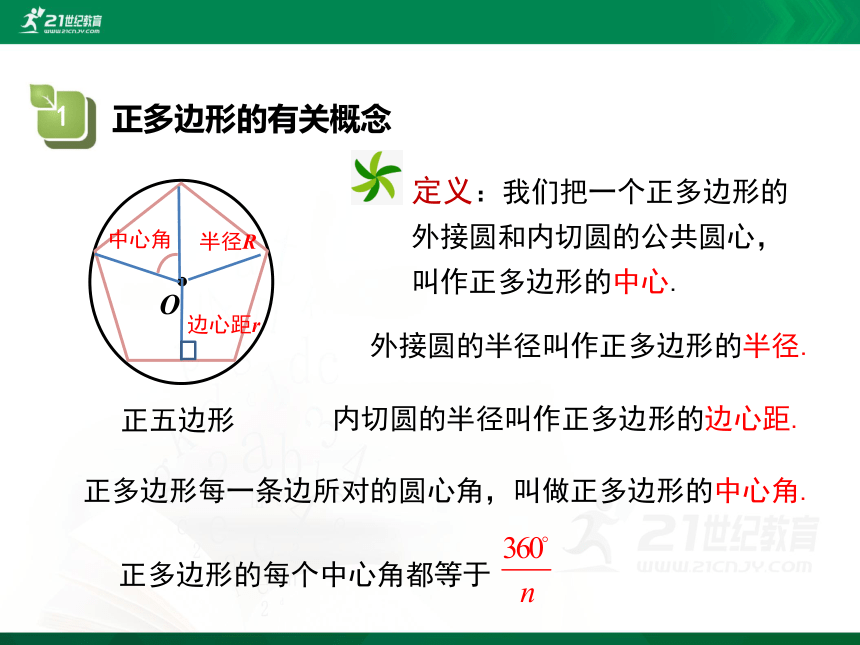
定义:我们把一个正多边形的外接圆和内切圆的公共圆心,叫作正多边形的中心.
外接圆的半径叫作正多边形的半径.
半径R
内切圆的半径叫作正多边形的边心距.
边心距r
正多边形每一条边所对的圆心角,叫做正多边形的中心角.
正多边形的每个中心角都等于
中心角
1
正多边形的有关概念
练一练:一个多边形的每一个内角均为108°,则这个多边形是( )
A.七边形
B.六边形
C.五边形
D.四边形
C
2
正多边形和圆的有关计算
例 如图,有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积 (结果保留小数点后一位).
E
A
B
C
D
F
O
2
正多边形和圆的有关计算
E
A
B
C
D
F
O
所以它的中心角等于360°÷6=60°,△OBC是等边三角形,而正六边形的边长等于它的半径.
解 如图所示 .连接OB,OC,
因为六边形ABCDEF是正六边形,
因此亭子地基的周长l=6×4=24(m)
过点O作OP⊥BC于P.
P
在Rt△OPC中,OC=4m,PC=2m
利用勾股定理,可得边心距
亭子地基的面积
2
正多边形和圆的有关计算
练一练:如图,正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )
A.
B.2
C.
D.
B
随堂练习
1.下列说法不正确的是( )
A.正多边形一定有一个外接圆
B.各边相等且各角相等的多边形一定是正多边形
C.正多边形的内切圆和外接圆是同心圆
D.正多边形既是轴对称图形又是中心对称图形
D
2.下列说法正确的有( )
①正n边形的中心角为 ;
②正n边形的内角为 ;
③正n边形的外角为 ;
④正n边形的半径为R,边心距r和边长an满足关系式:
.
A.1个 B.2个
C.3个 D.4个
D
3.若正方形的外接圆半径为2,则其内切圆半径为( )
A.
B.
C.
D.1
A
4.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A.
B.
C.
D.
A
5.如图,已知⊙O和⊙O上的一点A.
(1)作⊙O的内接正方形ABCD和内接正六边形AEFCGH;
(2)在(1)题的作图中,如果点E在AB上,
求证:BE是⊙O的内接正十二边形的一边.
∴BE是⊙O的内接正十二边形的一边.
(1)解 如图所示 .
H
E
F
C
G
D
B
(2)证明 连接OA.
由题意,得
∠BOA=90°,∠EOA=60°,
∴∠BOE=90°-60°=30°=360°÷12,
6.如图,已知正三角形ABC的边长为6,求它的中心角、半径和边心距.
B
A
C
解 设这个正三角形的中心为点O,
连接OB,OC,作OH⊥BC于点H,
则∠BOC=360°÷3=120°,
∴∠BOH=60°.
在Rt△BOH中,
BH= BC=3,∠OBH=30°,
2
1
∴OH= ,OB= .
∴正三角形ABC的中心角为120°,半径为 ,边心距为 .
O
H
课堂小结
正多边形和圆
正多边形的有关概念
正多边形和圆的有关计算
O
半径R
边心距r
中心角
添加辅助线的方法:
连半径,作边心距
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
24.3 正多边形和圆
课程讲授
新知导入
随堂练习
课堂小结
第二十四章 圆
知识要点
1.正多边形的有关概念
2.正多边形和圆的有关计算
新知导入
看一看:观察下图中图形的构成,试着发现它们的规律。
课程讲授
1
正多边形的有关概念
正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
正六边形
正方形
正五边形
1
正多边形的有关概念
以圆的内接正五边形为例证明.
E
A
B
C
D
正五边形
O
如图,把⊙O分成相等的5段弧,依次连接各分点得到五边形ABCDE.
∴AB=BC=CD=DE=EA
∴∠A=∠B
∵∠B=∠C=∠D=∠E
又 五边形ABCDE的顶点都在上,
∵AB=BC=CD=DE=EA
)
)
)
)
)
BCE=3AB=CDA
)
)
)
∴五边形ABCDE是⊙O的内接五边形,
⊙O是五边形ABCDE的外接圆.
1
正多边形的有关概念
正五边形
O
定义:我们把一个正多边形的外接圆和内切圆的公共圆心,叫作正多边形的中心.
外接圆的半径叫作正多边形的半径.
半径R
内切圆的半径叫作正多边形的边心距.
边心距r
正多边形每一条边所对的圆心角,叫做正多边形的中心角.
正多边形的每个中心角都等于
中心角
1
正多边形的有关概念
练一练:一个多边形的每一个内角均为108°,则这个多边形是( )
A.七边形
B.六边形
C.五边形
D.四边形
C
2
正多边形和圆的有关计算
例 如图,有一个亭子,它的地基是半径为4 m的正六边形,求地基的周长和面积 (结果保留小数点后一位).
E
A
B
C
D
F
O
2
正多边形和圆的有关计算
E
A
B
C
D
F
O
所以它的中心角等于360°÷6=60°,△OBC是等边三角形,而正六边形的边长等于它的半径.
解 如图所示 .连接OB,OC,
因为六边形ABCDEF是正六边形,
因此亭子地基的周长l=6×4=24(m)
过点O作OP⊥BC于P.
P
在Rt△OPC中,OC=4m,PC=2m
利用勾股定理,可得边心距
亭子地基的面积
2
正多边形和圆的有关计算
练一练:如图,正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )
A.
B.2
C.
D.
B
随堂练习
1.下列说法不正确的是( )
A.正多边形一定有一个外接圆
B.各边相等且各角相等的多边形一定是正多边形
C.正多边形的内切圆和外接圆是同心圆
D.正多边形既是轴对称图形又是中心对称图形
D
2.下列说法正确的有( )
①正n边形的中心角为 ;
②正n边形的内角为 ;
③正n边形的外角为 ;
④正n边形的半径为R,边心距r和边长an满足关系式:
.
A.1个 B.2个
C.3个 D.4个
D
3.若正方形的外接圆半径为2,则其内切圆半径为( )
A.
B.
C.
D.1
A
4.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )
A.
B.
C.
D.
A
5.如图,已知⊙O和⊙O上的一点A.
(1)作⊙O的内接正方形ABCD和内接正六边形AEFCGH;
(2)在(1)题的作图中,如果点E在AB上,
求证:BE是⊙O的内接正十二边形的一边.
∴BE是⊙O的内接正十二边形的一边.
(1)解 如图所示 .
H
E
F
C
G
D
B
(2)证明 连接OA.
由题意,得
∠BOA=90°,∠EOA=60°,
∴∠BOE=90°-60°=30°=360°÷12,
6.如图,已知正三角形ABC的边长为6,求它的中心角、半径和边心距.
B
A
C
解 设这个正三角形的中心为点O,
连接OB,OC,作OH⊥BC于点H,
则∠BOC=360°÷3=120°,
∴∠BOH=60°.
在Rt△BOH中,
BH= BC=3,∠OBH=30°,
2
1
∴OH= ,OB= .
∴正三角形ABC的中心角为120°,半径为 ,边心距为 .
O
H
课堂小结
正多边形和圆
正多边形的有关概念
正多边形和圆的有关计算
O
半径R
边心距r
中心角
添加辅助线的方法:
连半径,作边心距
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
