25.2 用列举法求概率 第1课时 课件

(共22张PPT)
25.2 用列举法求概率




课程讲授





















新知导入







随堂练习




课堂小结
第1课时 用列表法求概率
第二十五章 概率初步
知识要点
1.直接列举求概率
2.用列表法求概率
新知导入
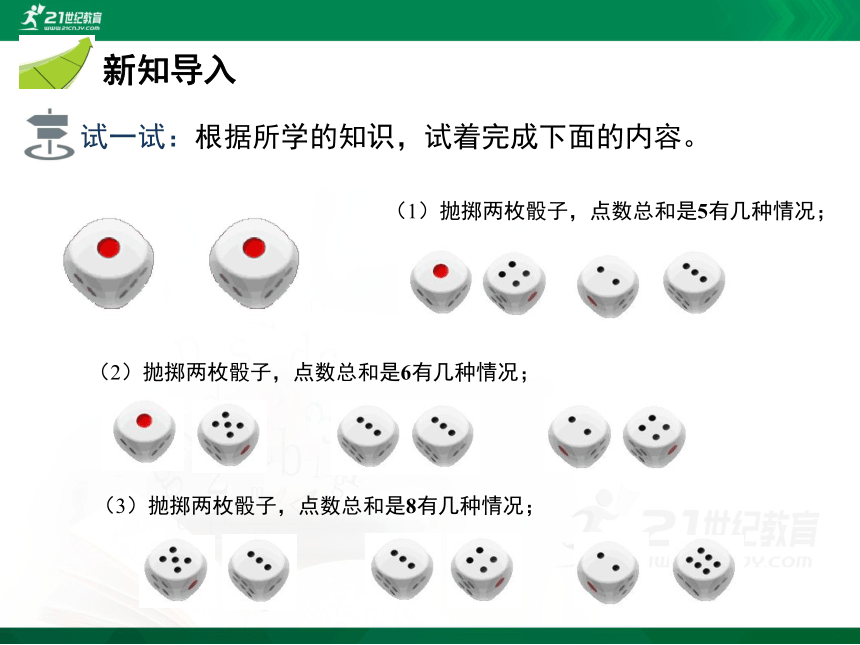
试一试：根据所学的知识，试着完成下面的内容。
（1）抛掷两枚骰子，点数总和是5有几种情况；
（2）抛掷两枚骰子，点数总和是6有几种情况；
（3）抛掷两枚骰子，点数总和是8有几种情况；
课程讲授
1
直接列举求概率
例 同时掷两枚硬币，试求下列事件的概率：
(1)两枚硬币全部正面向上；
(2)两枚硬币全部反面向上；
(3)一枚硬币正向上，一枚硬币反面向上.
1
直接列举求概率
我们可以发现：
存在四种可能的情况
1
直接列举求概率
解 （1）所有可能的结果中，满足两枚两枚硬币全部正面向上（记为事件A）的结果只有1种，即“正正”，所以
P（A）=
1
4
（2）两枚两枚硬币全部反面向上（记为事件B）的结果只有1种，即“反反”，所以
P（B）=
1
4
（3）一枚硬币正向上，一枚硬币反面向上（记为事件B）的结果只有2种，即“反正”“正反”，所以
P（B）= =
2
4
1
2
1
直接列举求概率
归纳： 直接列举法比较适合用于最多涉及两个试验因素或分两步进行的试验，且事件总结果的种数比较少的等可能性事件.
1
直接列举求概率
练一练：同时抛掷两枚质地均匀的硬币，两枚硬币全部正面向上的概率为（ ）
A.
B.
C.
D.
A
2
用列表法求概率
例 同时抛掷2枚均匀的骰子一次，骰子各面上的点数分别是1，2，···，6.试分别计算如下各随机事件的概率.
(1)抛出的点数相同；
(2)抛出的点数之和等于9；
(3)抛出的点数至少有一个为2.
提示：两枚骰子分别记作第一枚和第二枚，可以用表格列举出所以可能的结果.
2
用列表法求概率
1 2 3 4 5 6
1 （1,1） （2,1） （3,1） （4,1） （5,1） （6,1）
2 （1,2） （2,2） （3,2） （4,2） （5,2） （6,2）
3 （1,3） （2,3） （3,3） （4,3） （5,3） （6,3）
4 （1,4） （2,4） （3,4） （4,4） （5,4） （6,4）
5 （1,5） （2,5） （3,5） （4,5） （5,5） （6,5）
6 （1,6） （2,6） （3,6） （4,6） （5,6） （6,6）




2
用列表法求概率
解 从上表可以看出，同时抛掷两枚骰子一次，所有可能出现的结果有36种.由于骰子是均匀的，所以每个结果出现的可能性相等.
(1)抛出点数相同（记为事件A）的结果有(1,1),(2,2),(3,3),(4,4),(5,5)和(6,6)这6种，所以抛出的点数之和等于8的这个事件发生的概率为
(2)抛出点数之和（记为事件B）等于9的结果有(3,6),(4,5),(5,4)和(6,3)这4种，所以抛出的点数之和等于12的这个事件发生的概率为
P（A）= =
6
36
1
6
P（B）= =
4
36
1
9
(2)抛出点数至少有一个为2（记为事件C）等于9的结果有(2,1),(2,2),(2,3),(2,4)，(2,5)，(2,6),(1,2),(1,2),(3,2),(4,2),(5,2),(6,2),和这11种，所以抛出的点数之和等于12的这个事件发生的概率为
P（C）=
11
36
2
用列表法求概率
归纳： 当一次试验要涉及两个因素（例如掷两个骰子）并且可能出现的结果数目较多时，为不重不漏地列出所有可能结果，通常采用列表法.
2
用列表法求概率
练一练：从-2，-1，2这三个数中任取两个不同的数相乘，积为正数的概率是（ ）
A.
B.
C.
D.
C
随堂练习
1.从2，3，4中任选两个不同数字组成一个两位数，组成的数是偶数的概率是（ ）
A.
B.
C.
D.
A
2.一个不透明的袋子中有三个完全相同的小球，把它们分别标号为1，2，3，随机摸出一个小球，记下标号后放回，再随机摸出一个小球并记下标号，两次摸出的小球标号的和是偶数的概率是（ ）
A.
B.
C.
D.
D
3.四张背面完全相同的卡片上正面分别印有等腰三角形、平行四边形、菱形、圆的图案，现将印有图案的一面朝下，混合后从中随机抽取两张，则抽到卡片上印有的图案都是轴对称图形的概率是（ ）
A.
B.
C.
D.
D
4.让图中两个转盘分别自由转动一次，当转盘停止转动时，两个指针分别落在某两个数所表示的区域，则这两个数的和是2的倍数或是3的倍数的概率等于（ ）
A.
B.
C.
D.
C
5.现有四张完全相同的卡片，上面分别标有数字-1，-2，3，4.把卡片背面朝上洗匀，然后从中随机抽取两张，则这两张卡片上的数字之积为负数的概率是_____.
3
2
6.有4根细木棒，长度分别为2 cm，3 cm，4 cm，5 cm，从中任选3根，恰好能搭成一个三角形的概率是______.
4
3
7.一只不透明的袋子中装有白球2个和黄球1个，这些球除颜色外都相同，搅匀后从中任意摸出1个球，记下颜色后不放回，搅匀后再从中任意摸出1个球，请用列表的方法求两次都摸出白球的概率.
解 列表如下：
共有6种等可能结果，其中都为白球的结果有2种，
∴P(都为白球)= = .
6
2
3
1
课堂小结
用列举法求概率
直接列举
列表法


适合用于最多涉及两个试验因素或分两步进行的试验，且事件总结果的种数比较少的等可能性事件.

适合涉及两个因素（例如掷两个骰子）并且可能出现的结果数目较多的等可能性事件
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php