沪科版七年级数学上册第二章整式加减单元测试卷含解析
文档属性
| 名称 | 沪科版七年级数学上册第二章整式加减单元测试卷含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-24 16:43:40 | ||
图片预览




文档简介
整式加减单元测试卷
考试范围:第2章;考试时间:120分钟;
一、单选题(每题4分共40分)
1.下列关于单项式的说法中,正确的是( )
A.系数是3,次数是2 B.系数是,次数是2
C.系数是,次数是3 D.系数是,次数是3
2.下列运算中,正确的是( )
A.x2y﹣yx2=0????????????????????? B.2x2+x2=3x4??????????????????????????? C.4x+y=4xy????????????????????? D.2x﹣x=1
3.若m=﹣1,n=2,则m2﹣2n+1的值是( )
A.6 B.0 C.﹣2 D.﹣4
4.某种商品进价为每件a元,销售商先以高出进价50%定价后又以7折的价格销售,这时一件该商品的在买卖过程中盈亏情况为( )
A.赢利0.05a元 B.赢利0.5a元 C.亏损0.05a元 D.亏损0.3a元
5.如图,有四个大小相同的小长方形和两个大小相同的大长方形按如图位置摆放,按照图中所示尺寸,则小长方形的长与宽的差是( )
A. B. C. D.
6.如果=0, 那么代数式的值是( )
A.1 B.-1 C.±1 D.2008
7.一个两位数x,还有一个两位数y,若把两位数x放在y前面,组成一个四位数,则这个四位数为( )
A.10x+y???????????????????????????????? B.xy???????????????????????????????? C.100x+y???????????????????????????????? D.1000x+y
8.已知,则代数式的值为
A.18 B.14 C.6 D.2
9.减去-2m等于m2+3m+2多项式是( )
A.m2+5m+2????????????????????????? B.m2+m+2????????????????????????? C.m2-5m-2????????????????????????? D.m2-m-2
10.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”.如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形”之和,下列等式中,符合这一规律的表达式为( )
A. B. C. D.
二、填空题(每题5分共40分)
11.已知单项式-2am+1b3与单项式3a3bn-2是同类项,则nm=_________.
12.若a+b=5,ab=3,则(a﹣2)(b﹣2)=________
13.如图,是一个用四块形状和大小都一样的长方形纸板拼成的一个大正方形,中间空的部分是—个小正方形,已知长方形纸板的长为m,宽为n(m>n),则中间空的部分(小正方形)的面积是___________。
14.观察下列算式:12= ,12+22= ,12+22+32= ,12+22+32+42= ,…,请用字母表示数,将你发现的一般规律用一个等式表示出来:________.
三、解答题(各题分值分别为:8、8、8、8、10、10、12、12、14分,满分90分)
15.计算:﹣12016×[(﹣2)5﹣32﹣÷(﹣)]﹣2.5.
16.先去括号,再合并同类项4a2+2(3ab﹣2a2)﹣(7ab﹣1)
17.已知,求的值.
18.已知,,计算当时,的值.
19.你坐过出租车吗?请你帮小明算一算,某市出租车收费标准是:起步价(3千米以内)10元,超过3千米的部分每千米1.20元,小明爸爸乘坐了x(x为整数,且x>3)千米的路程.
(1)请你用含x的代数式表示他应支付的车费钱数;
(2)若他支付的费用是23.2元,你能算出他乘坐的路程吗?
20.观察下列等式
,,,
将以上三个等式两边分别相加得:
.
(1)猜想并写出:_____________.
(2)直接写出下列各式的计算结果:
①______________;
②______________.
(3)探究并计算:.
21.某种水果第一天以3元的价格卖出a斤,第二天以2元的价格卖出b斤,第三天以1元的价格卖出c斤,求(用含a, b, c的式子表示):
(1)这三天共卖出水果多少斤?
(2)这三天共卖得多少元?
22.如图,当x=5.5,y=4时,求阴影部分的周长和面积.
23.数学问题:计算(其中m,n都是正整数,且m≥2,n≥1).
探究问题:为解决上面的数学问题,我们运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来,并采取一般问题特殊化的策略来进行探究.
探究一:计算.
第1次分割,把正方形的面积二等分,其中阴影部分的面积为;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为+;
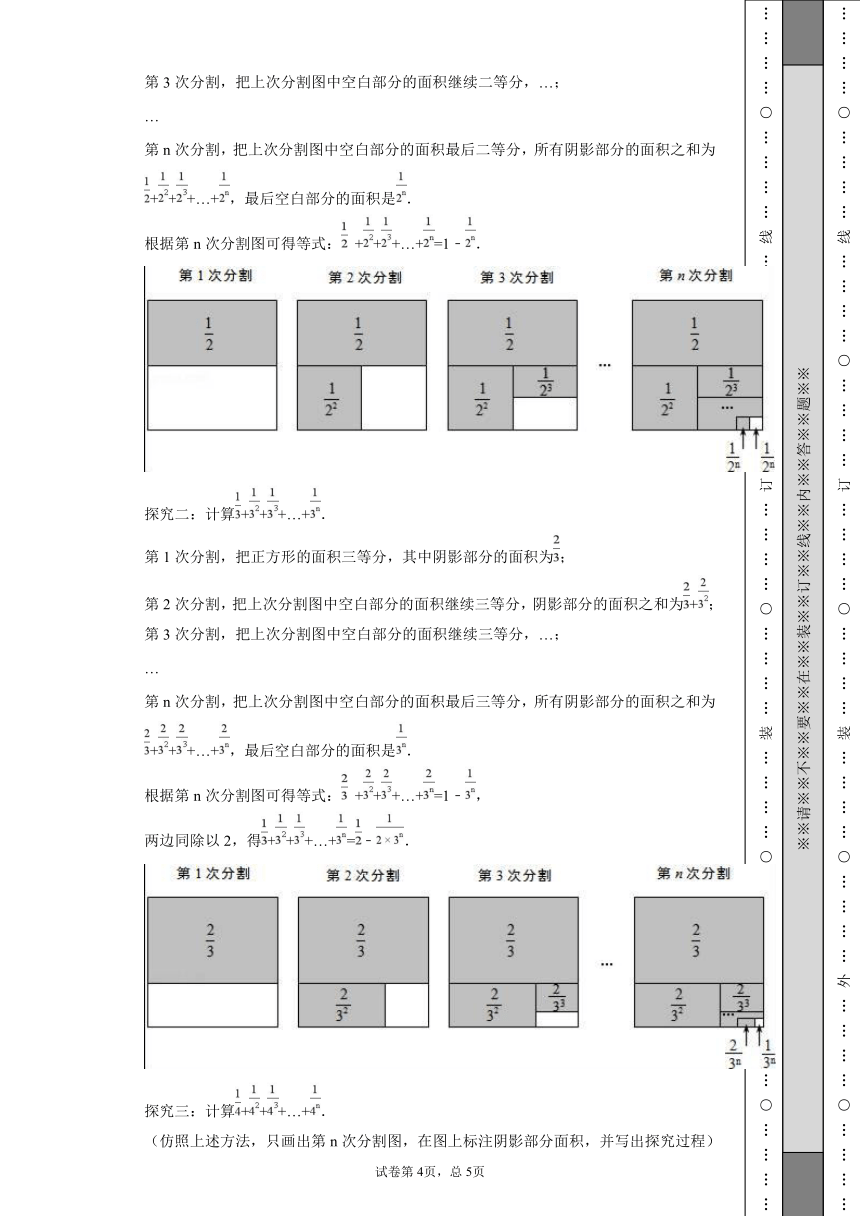
第3次分割,把上次分割图中空白部分的面积继续二等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为+++…+,最后空白部分的面积是.
根据第n次分割图可得等式: +++…+=1﹣.
探究二:计算+++…+.
第1次分割,把正方形的面积三等分,其中阴影部分的面积为;
第2次分割,把上次分割图中空白部分的面积继续三等分,阴影部分的面积之和为+;
第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后三等分,所有阴影部分的面积之和为+++…+,最后空白部分的面积是.
根据第n次分割图可得等式: +++…+=1﹣,
两边同除以2,得+++…+=﹣.
探究三:计算+++…+.
(仿照上述方法,只画出第n次分割图,在图上标注阴影部分面积,并写出探究过程)
解决问题:计算+++…+.
(只需画出第n次分割图,在图上标注阴影部分面积,并完成以下填空)
根据第n次分割图可得等式:_________,
所以, +++…+=________.
拓广应用:计算 +++…+.
参考答案
1.D
【解析】
解:根据单项式系数、次数的定义可知,单项式的系数是,次数是3.故选D.
2.A
【解析】
【分析】
直接利用合并同类项法则分别判断得出答案.
【详解】
A、x2y?yx2=0,正确;
B、2x2+x2=3x2,故此选项错误;
C、4x+y无法计算,故此选项错误;
D、2x?x=x,故此选项错误.
故选:A.
【点睛】
此题主要考查了合并同类项法则,正确掌握运算法则是解题关键.
3.C
【解析】试题解析:把m=﹣1,n=2代入m2﹣2n+1得:
原式=(-1)2-2×2+1
=-2.
故选C.
4.A
【解析】
【分析】
总售价?总成本,结果为正数,是盈利;结果是负数,是亏损.
【详解】
总售价=a(1+50%)×0.7=1.05a,
∵1.05a?a=0.05a,
∴赢利0.05a元,
故选:A.
【点睛】
本题考查了根据实际问题列代数式,并求代数式的值,把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.本题解题的关键是读懂题意,正确列出代数式.盈利与否应看售价与成本的比较.
5.A
【解析】
【分析】
设小长方形的长为x,宽为y,根据题意求出x﹣y的值,即为长与宽的差.
【详解】
设小长方形的长为x,宽为y,根据题意得:a+y﹣x=b+x﹣y,即2x﹣2y=a﹣b,整理得:x﹣y,则小长方形的长与宽的差是.
故选A.
【点睛】
本题考查了整式的加减,熟练掌握运算法则是解答本题的关键.
6.A
【解析】
【分析】
根据非负数的性质:几个非负数的和等于0,则每个式子等于0,据此即可列方程求得a和b的值,进而求解.
【详解】
解:根据题意得:,
解得:,
则原式=(-2+1)2014=1.
故选:A.
【点睛】
本题考查了非负数的性质,几个非负数的和等于0,则每个式子等于0,理解性质是关键.
7.C
【解析】
【分析】
把两位数x放在y前面,组成一个四位数,相当于把x扩大了100倍.
【详解】
根据题意,得这个四位数是100x+y.
故选:C.
【点睛】
此题考查了用字母表示数的方法,理解数位的意义.
8.A
【解析】
【分析】
原式变形后,将已知等式代入计算即可求出值.
【详解】
解:,
原式,
故选:A.
【点睛】
本题考查代数式求值,熟练掌握运算法则是解本题的关键.
9.B
【解析】
【分析】
设这个多项式为A,再根据题意列出多项式相加减的式子,去括号,合并同类项即可.
【详解】
设这个多项式为A,
则A=(m2+3m+2)+(?2m)=m2+3m+2?2m=m2+m+2.
故选:B.
【点睛】
本题考查的是整式的加减,熟知整式的加减实质上就是合并同类项是解答此题的关键.
10.D
【解析】
【分析】
三角形数=1+2+3+……+n,很容易就可以知道一个数是不是三角形数.结合公式,代入验证三角形数就可以得到答案.
【详解】
A.中3和10是三角形数,但是不相邻;
B.中16、9均是正方形数,不是三角形数;
C.中18不是三角形数;
D.中28=1+2+3+4+5+6+7,36=1+2+3+4+5+6+7+8,所以D正确;
故选D.
【点睛】
此题考查此题考查规律型:数字的变化类,勾股数,解题关键在于找到变换规律.
11.25
【解析】
【分析】
如果两个单项式,它们所含的字母相同,并且相同字母的指数也分别相同,那么就称这两个单项式为同类项,根据同类项的定义,把握“两相同”解题.
【详解】
解:
,
故答案是:25.
【点睛】
本题考查同类项的定义,解题的关键是熟练运用同类项的定义,本题属于基础题型.
12.-3
【解析】
试题解析:(a-2)(b-2)=ab-2(a+b)+4
∵a+b=5,ab=3,
∴原式=3-10+4=-3.
13.(m-n)2或(m+n)2-4mn
【解析】
试题分析:
解:由题意知中间空的部分是小正方形,故,S=
或者用大正方形的面积减去阴影部分的面积,即得
考点:代数式运算
点评:此类试题是常考点,考生务必对其熟练把握才可以在以后的类似情况中分析出来
14.12+22+32+…+n2=
【解析】
【分析】
观察不难发现,从1开始的平方数的和,分母都是6,分子为最后一个数与比它大1的数的积再乘以比这个数的2倍大1的数的积,根据规律写出含n的算式即可.
【详解】
12+22+32+…+n2==.
故答案为:.
【点睛】
此题考查数字的变化规律,难点在于观察出分子的变化情况.
15.36
【解析】试题分析:原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
试题解析:原式=﹣1×(﹣32﹣9+2.5)﹣2.5=41﹣5=36.
16.-ab+1
【解析】
【分析】
根据去括号法则去掉式子中的括号,再合并同类项,可得答案.
【详解】
4a2+2(3ab﹣2a2)﹣(7ab﹣1)=4a2+6ab﹣4a2﹣7ab+1=﹣ab+1.
【点睛】
本题考查了去括号与合并同类项,括号前是正号去掉括号不变号,括号前是负号去掉括号要变号.
17.
【解析】
试题分析:根据偶次幂和绝对值的非负性质,由求出,代入化简后代数式求解即可.
∵,∴.
∴
.
考点:1.代数式求值;2.偶次幂和绝对值的非负性质.
18.
【解析】
【分析】
先将A和B的代数式代入(3A-B)进行化简,然后再代入a的具体数值求解.
【详解】
解:原式=3×()-()= 3×+-6a+4a+3-2=6a3-2a+1
代入a=-1,则原式=6×(-1)3-2×(-1)+1=-3.
即, .
【点睛】
本题主要考察了先化简整式,再代入求值.
19.(1) 1.2x+6.4(元);(2)14千米
【解析】
【分析】
(1)用起步价加上超过3千米的费用即可;
(2)由(1)中的代数式列出方程解答即可.
【详解】
(1)解:10+1.2(x﹣3)=1.2x+6.4(元)
(2)解:1.2x+6.4=23.2,
解得:x=14.
答:他乘坐的路程是14千米
【点睛】
此题考查列代数式,理解题意,找出题目蕴含的数量关系解决问题.
20.(1);(2)①;②;(3).
【解析】分析:
(1)观察、分析所给等式可知:;
(2)①②根据(1)中所得规律进行计算即可;
(3)根据等式将原式变形,再进行计算即可.
详解:
(1)观察、分析所给等式可得:;
(2)① 原式=
=
=;
② 原式=
=
=;
(3)原式=
=
=
=
=.
点睛:(1)根据题中所给等式,分析得到:“当n为正整数时,等式成立”是解答第1、2小题的关键;(2)知道:“当n为正整数时,等式成立”是解答第3小题的关键.
21.(1)(a+b+c)斤;(2)(3a+2b+c)元.
【解析】
【分析】
(1)把三天所卖的斤数相加即可;
(2)把每天所卖的钱数相加即可.
【详解】
(1)这三天共卖出水果(a+b+c)斤;
(2)这三天共卖得(3a+2b+c)元.
【点睛】
本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式. 列代数式五点注意:仔细辨别词义.?认真审题,抓住关键词语,仔细辩析词义,分清数量之间的关系.
22.阴影部分的周长为46,阴影部分的面积为77.
【解析】
【分析】
根据周长的定义列式,然后把x、y的值代入进行计算即可得解;
用长方形的面积减去缺口的面积,再把x、y的值代入进行计算即可得解.
【详解】
阴影部分的周长为=2(2x+2y)+2y
∵x=5.5,y=4,
∴周长=4×5.5+6×4=22+24=46;
阴影部分的面积=2x?2y-y(2x-0.5x-x)=4xy-0.5xy=3.5xy,
∵x=5.5,y=4,
∴面积=3.5×5.5×4=77.
【点睛】
本题考查了列代数式,代数式求值,主要利用了周长与面积的定义,仔细观察图形,得到面积的表示是解题的关键.
23.
【解析】
【分析】
探究三:根据探究二的分割方法依次进行分割,然后表示出阴影部分的面积,再除以3即可;
解决问题:按照探究二的分割方法依次分割,然后表示出阴影部分的面积及,再除以(m-1)即可得解;
拓广应用:先把每一个分数分成1减去一个分数,然后应用公式进行计算即可得解.
【详解】
探究三:第1次分割,把正方形的面积四等分,
其中阴影部分的面积为;
第2次分割,把上次分割图中空白部分的面积继续四等分,
阴影部分的面积之和为;
第3次分割,把上次分割图中空白部分的面积继续四等分,
…,
第n次分割,把上次分割图中空白部分的面积最后四等分,
所有阴影部分的面积之和为:,
最后的空白部分的面积是,
根据第n次分割图可得等式:=1﹣,
两边同除以3,得=;
解决问题:=1﹣,
=;
故答案为:=1﹣,;
拓广应用:,
=1﹣+1﹣+1﹣+…+1﹣,
=n﹣(+++…+),
=n﹣(﹣),
=n﹣+.
【点睛】
本题考查了应用与设计作图,图形的变化规律,读懂题目信息,理解分割的方法以及求和的方法是解题的关键.
试卷第4页,总5页
试卷第5页,总5页
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
