1.1.6 棱柱、棱锥、棱台和球的表面积 31张
文档属性
| 名称 | 1.1.6 棱柱、棱锥、棱台和球的表面积 31张 |

|
|
| 格式 | zip | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 00:00:00 | ||
图片预览



文档简介
(共31张PPT)
第一章 §1.3 空间几何体的表面积与体积
学习目标
1.通过对柱、锥、台体的研究,掌握柱、锥、台体的表面积的求法.
2.了解柱、锥、台体的表面积和体积计算公式;能运用柱、锥、台的表面积和体积公式进行计算和解决有关实际问题.
学习目标
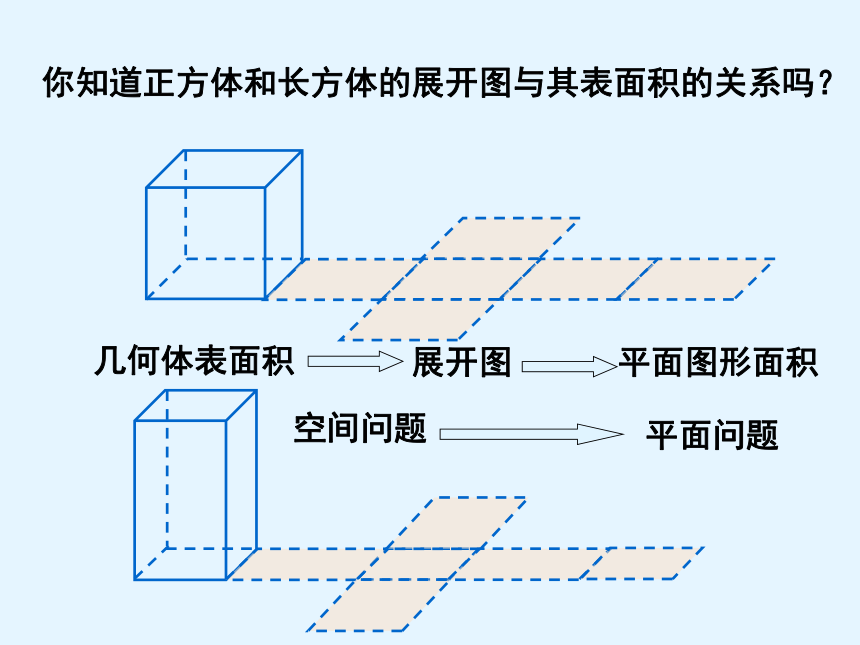
你知道正方体和长方体的展开图与其表面积的关系吗?
几何体表面积
各个面
展开图
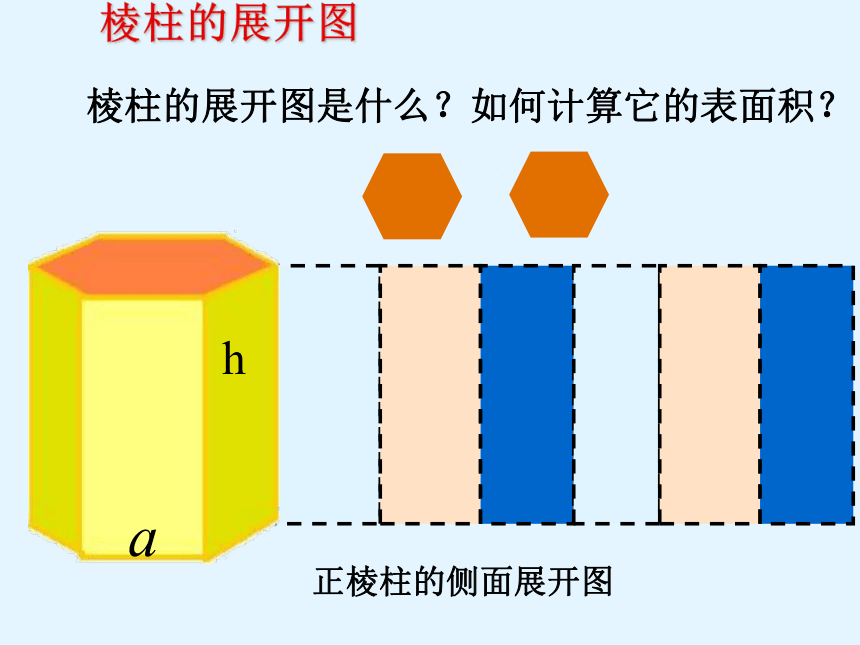
棱柱的展开图是什么?如何计算它的表面积?
h
棱柱的展开图
正棱柱的侧面展开图
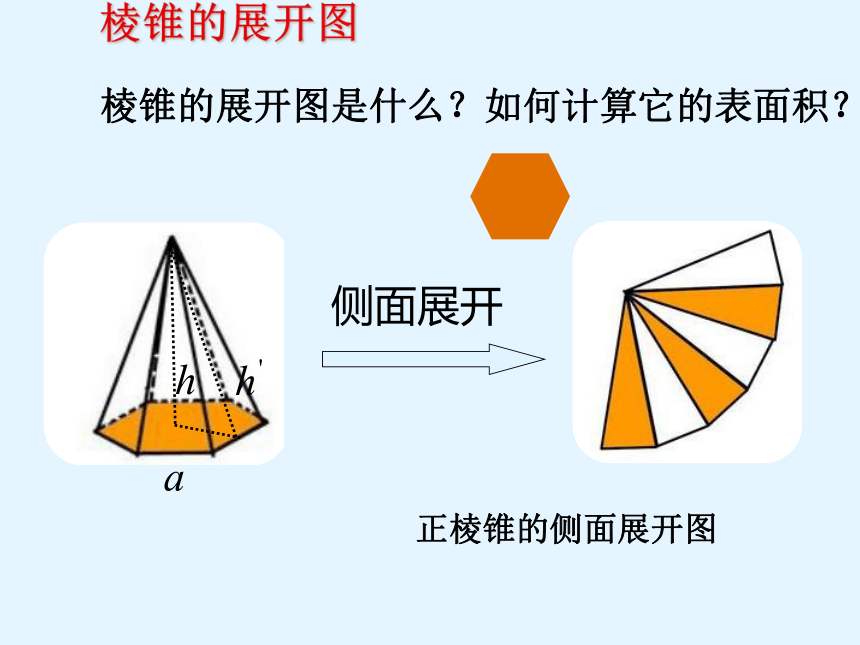
棱锥的展开图是什么?如何计算它的表面积?
棱锥的展开图
侧面展开
正棱锥的侧面展开图
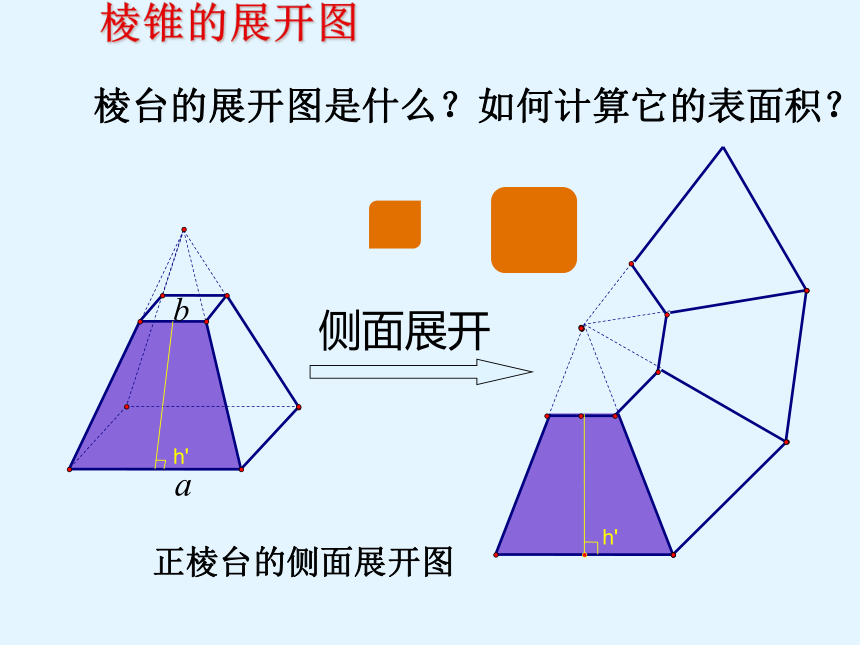
棱台的展开图是什么?如何计算它的表面积?
棱锥的展开图
侧面展开
正棱台的侧面展开图
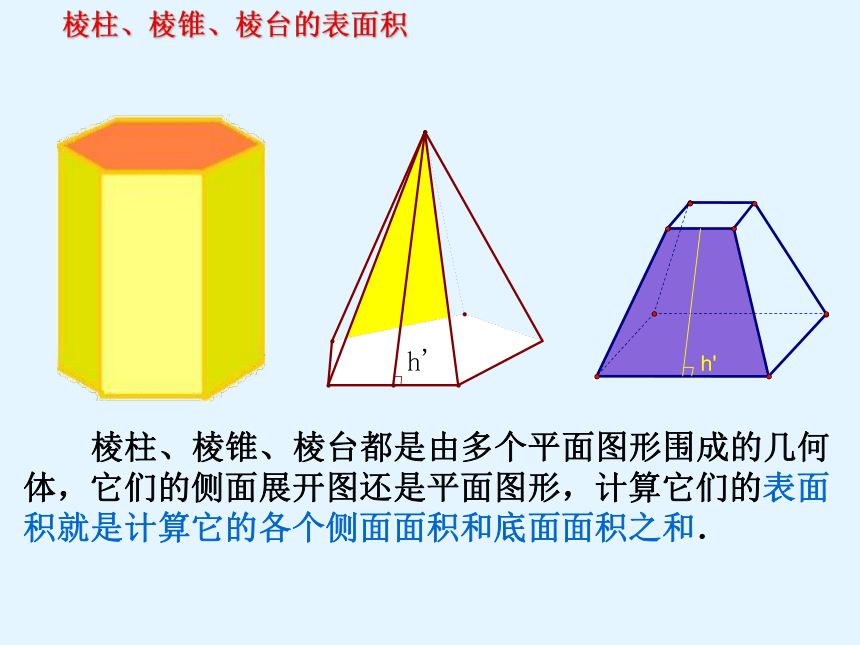
棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和.
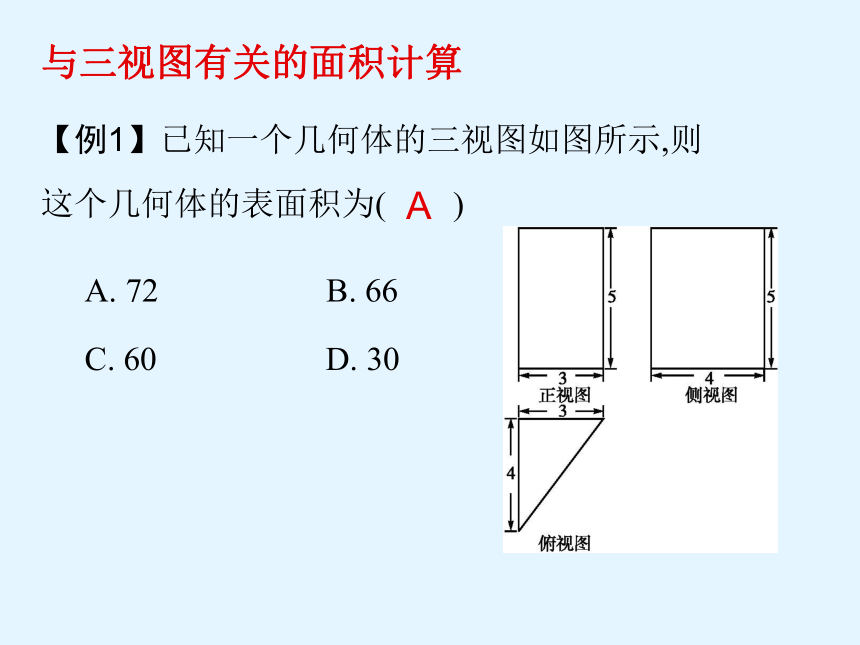
【例1】已知一个几何体的三视图如图所示,则这个几何体的表面积为( )
A. 72 B. 66
C. 60 D. 30
A
与三视图有关的面积计算
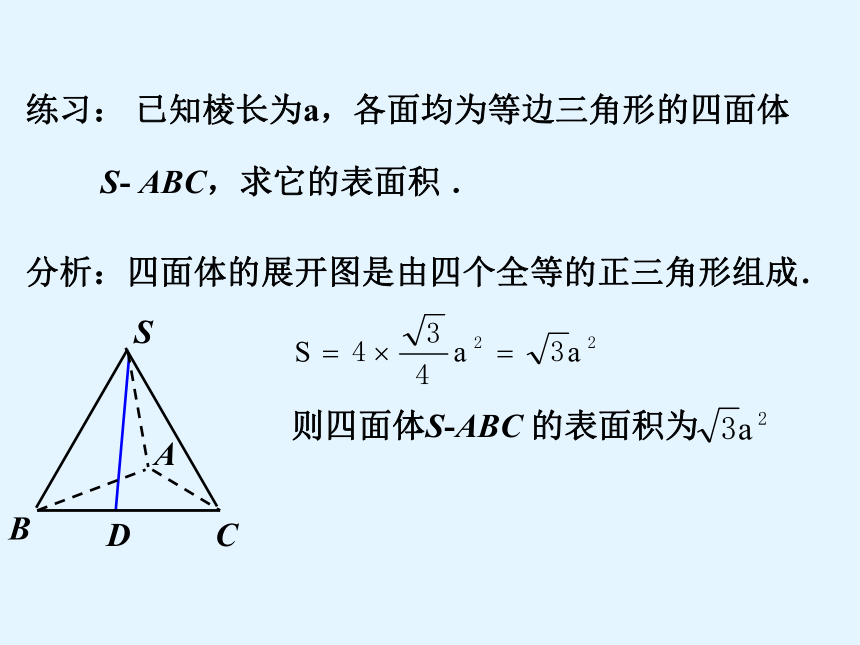
练习: 已知棱长为a,各面均为等边三角形的四面体
S- ABC,求它的表面积 .
分析:四面体的展开图是由四个全等的正三角形组成.
则四面体S-ABC 的表面积为
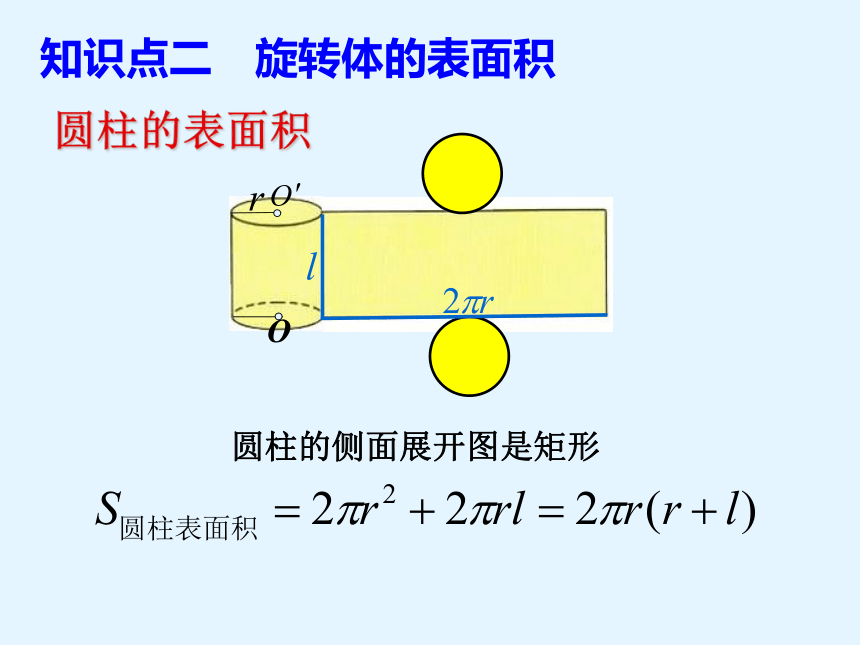
圆柱的表面积
圆柱的侧面展开图是矩形
知识点二 旋转体的表面积
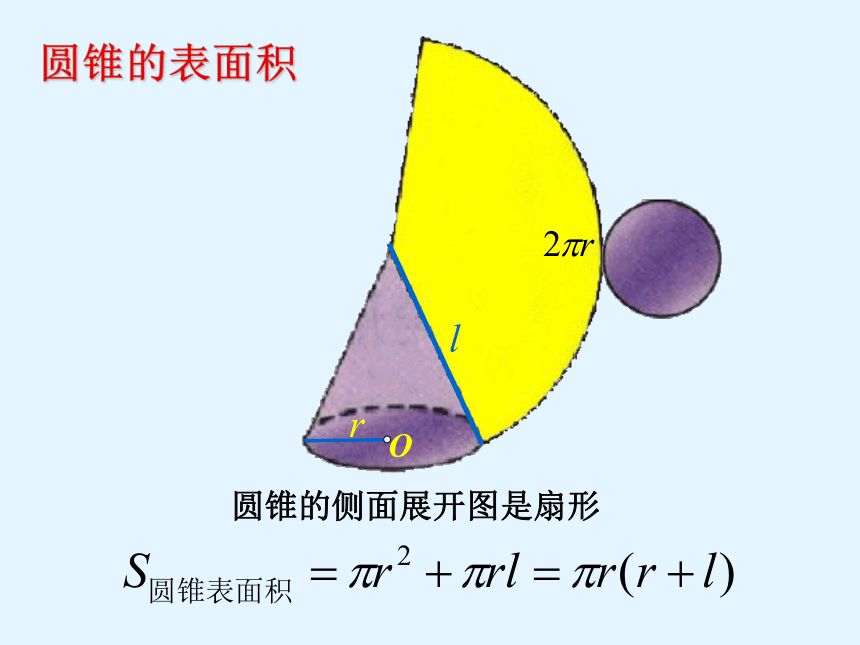
圆锥的表面积
圆锥的侧面展开图是扇形
圆台的表面积
参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么 .
圆台的侧面展开图是扇环
三者之间关系
圆柱、圆锥、圆台三者的表面积公式之间有什么关系?
知识梳理 自主学习
知识点一 多面体的表面积
多面体的表面积就是 的面积的和,也就是 的面积.
知识点二 旋转体的表面积
展开图
各个面
2πr2
2πrl
2πrl+2πr2
名称 图形 公式
圆柱 底面积:S底=____
侧面积:S侧=____
表面积:S=__________
πrl+πr2
π(r' 2+r2+r' l+r l)
πr2
πrl
πr' 2
πr2
π(r+r' )l
圆锥 底面积:S底=___
侧面积:S侧=___
表面积:S=________
圆台 上底面面积:S上底=______
下底面面积:S下底=___
侧面积:S侧=__________
表面积:S=___________________
解:由圆台的表面积公式得
花盆的表面积:
典型例题
练习:直角三角形的两直角边AB=3, AC=4 ,以AB为轴旋转所得几何体的表面积为?
以前学过特殊的棱柱——正方体、长方体以及圆柱的体积公式,它们的体积公式可以统一为:
柱体体积
锥体体积
棱台(圆台)的体积公式
台体体积
柱体、锥体、台体的体积公式之间有什么关系?
S为底面面积,h为柱体高
S分别为上、下底面面积,h 为台体高
S为底面面积,h为锥体高
台体体积
题型三 与三视图有关的体积问题
例3 某几何体的三视图如图所示(单位:cm),则该几何体的体积等于
( )cm
A. 8π B. C. (5+ )π D. 6π
B
练习:一个几何体的三视图如图所示(单位:m),则该几何体的体积为______m3.
解析 由三视图可知该几何体是组合体.
下面是长方体,长、宽、高分别为3,2,1;
上面是一个圆锥,底面圆半径为1,高为3,
6+π
柱体、锥体、台体的表面积
知识小结
柱体、锥体、台体的体积
知识小结
1 . 若一个圆柱的侧面展开图是一个正方形,
则这个圆柱的全面积与侧面积的比是( )
A .
B .
C .
D .
A
四. 清理过关,课堂测评:
2.一个几何体的三视图及其尺寸如图(单位:cm),则该几何体的表面积为( )
A.12π B.18π
C.24π D.36π
解析 由三视图知该几何体为圆锥,底面半径r=3,母线l=5,
∴S表=πrl+πr2=24π.故选C.
C
3.如图,在棱长为a的正方体ABCD-A1B1C1D1中,
求三棱锥A-A1BD高.
解:
练习:书P27练习 1、2
作业:习题1.3 2、 3
第一章 §1.3 空间几何体的表面积与体积
学习目标
1.通过对柱、锥、台体的研究,掌握柱、锥、台体的表面积的求法.
2.了解柱、锥、台体的表面积和体积计算公式;能运用柱、锥、台的表面积和体积公式进行计算和解决有关实际问题.
学习目标
你知道正方体和长方体的展开图与其表面积的关系吗?
几何体表面积
各个面
展开图
棱柱的展开图是什么?如何计算它的表面积?
h
棱柱的展开图
正棱柱的侧面展开图
棱锥的展开图是什么?如何计算它的表面积?
棱锥的展开图
侧面展开
正棱锥的侧面展开图
棱台的展开图是什么?如何计算它的表面积?
棱锥的展开图
侧面展开
正棱台的侧面展开图
棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和.
【例1】已知一个几何体的三视图如图所示,则这个几何体的表面积为( )
A. 72 B. 66
C. 60 D. 30
A
与三视图有关的面积计算
练习: 已知棱长为a,各面均为等边三角形的四面体
S- ABC,求它的表面积 .
分析:四面体的展开图是由四个全等的正三角形组成.
则四面体S-ABC 的表面积为
圆柱的表面积
圆柱的侧面展开图是矩形
知识点二 旋转体的表面积
圆锥的表面积
圆锥的侧面展开图是扇形
圆台的表面积
参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么 .
圆台的侧面展开图是扇环
三者之间关系
圆柱、圆锥、圆台三者的表面积公式之间有什么关系?
知识梳理 自主学习
知识点一 多面体的表面积
多面体的表面积就是 的面积的和,也就是 的面积.
知识点二 旋转体的表面积
展开图
各个面
2πr2
2πrl
2πrl+2πr2
名称 图形 公式
圆柱 底面积:S底=____
侧面积:S侧=____
表面积:S=__________
πrl+πr2
π(r' 2+r2+r' l+r l)
πr2
πrl
πr' 2
πr2
π(r+r' )l
圆锥 底面积:S底=___
侧面积:S侧=___
表面积:S=________
圆台 上底面面积:S上底=______
下底面面积:S下底=___
侧面积:S侧=__________
表面积:S=___________________
解:由圆台的表面积公式得
花盆的表面积:
典型例题
练习:直角三角形的两直角边AB=3, AC=4 ,以AB为轴旋转所得几何体的表面积为?
以前学过特殊的棱柱——正方体、长方体以及圆柱的体积公式,它们的体积公式可以统一为:
柱体体积
锥体体积
棱台(圆台)的体积公式
台体体积
柱体、锥体、台体的体积公式之间有什么关系?
S为底面面积,h为柱体高
S分别为上、下底面面积,h 为台体高
S为底面面积,h为锥体高
台体体积
题型三 与三视图有关的体积问题
例3 某几何体的三视图如图所示(单位:cm),则该几何体的体积等于
( )cm
A. 8π B. C. (5+ )π D. 6π
B
练习:一个几何体的三视图如图所示(单位:m),则该几何体的体积为______m3.
解析 由三视图可知该几何体是组合体.
下面是长方体,长、宽、高分别为3,2,1;
上面是一个圆锥,底面圆半径为1,高为3,
6+π
柱体、锥体、台体的表面积
知识小结
柱体、锥体、台体的体积
知识小结
1 . 若一个圆柱的侧面展开图是一个正方形,
则这个圆柱的全面积与侧面积的比是( )
A .
B .
C .
D .
A
四. 清理过关,课堂测评:
2.一个几何体的三视图及其尺寸如图(单位:cm),则该几何体的表面积为( )
A.12π B.18π
C.24π D.36π
解析 由三视图知该几何体为圆锥,底面半径r=3,母线l=5,
∴S表=πrl+πr2=24π.故选C.
C
3.如图,在棱长为a的正方体ABCD-A1B1C1D1中,
求三棱锥A-A1BD高.
解:
练习:书P27练习 1、2
作业:习题1.3 2、 3
