必修2第一章 立体几何初步 1.1.2棱柱、棱锥、棱台和球的表面积(第一课时) 18张
文档属性
| 名称 | 必修2第一章 立体几何初步 1.1.2棱柱、棱锥、棱台和球的表面积(第一课时) 18张 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 16:55:19 | ||
图片预览






文档简介
(共18张PPT)
课前预习
1.直棱柱的定义________________________.
2.正棱锥的定义_____________________________________
_____________________________________.
3.正棱台的定义______________________.
4.直棱柱的侧面展开图是______;
正棱锥的侧面展开图是____________________;
正棱台的侧面展开图是____________________.
矩形
一些全等的等腰三角形
一些全等的等腰梯形
侧棱与底面垂直的棱柱
底面是正多边形,顶点在过底面中心且与底面垂直的直线上
由正棱锥截得的棱台
水立方
第一章——第一节空间几何体
1.1.6 棱柱、棱锥、棱台和球的表面积
一、直棱柱、正棱锥、正棱台的表面积
分析直六棱柱和正四棱锥的展开图
h
h
c
1.S直棱柱侧=ch
直棱柱的侧面积等于它的底面周长和高的乘积.
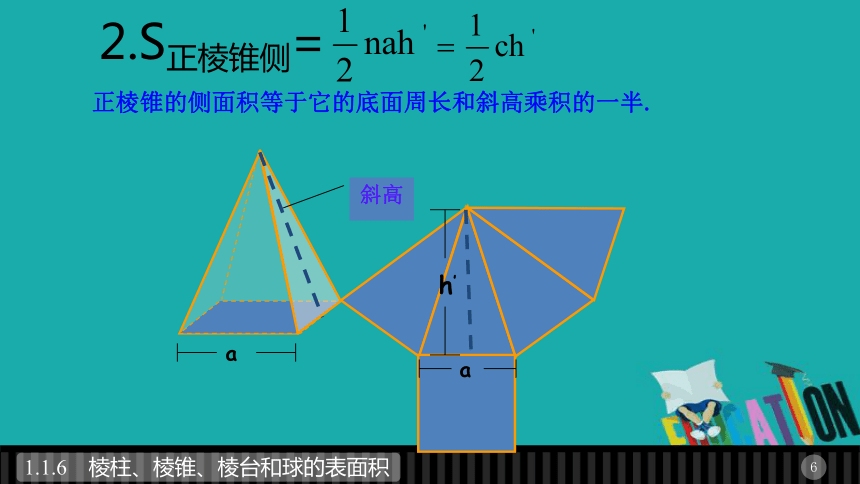
2.S正棱锥侧=
正棱锥的侧面积等于它的底面周长和斜高乘积的一半.
h’
斜高
a
a
正棱台的表面积
正棱台:
由正棱锥截得的棱台
分析正四棱台的展开图
3.S正棱台侧=
h’
a
a’
例1 已知正四棱锥底面边长为4,高与斜高夹角为30°,求它的侧面积和表面积.
解: 如图,正四棱锥的高为PO,
斜高为PE,底面边心距为OE,
它们组成一个直角三角形POE.
S表面积=42+32=48.
即该正四棱锥的侧面积是32,表面积是48.
变式:已知正四棱锥的斜高为4,高与斜高夹角为30°,求它的侧面积及全面积.
解:
已知正四棱台的上、下底面边长分别是2和4,高是2,求这个棱台的侧面积.
问题再探究
解:
1.已知正六棱柱的高为5 cm,最长的对角线长为13 cm,试求其侧面积.
课堂练习
解:
底面是菱形的直四棱柱中,它的对角线长为9和15,高是5,则直四棱柱的侧面积为___________
易错提示
解:
2.正四棱锥的侧面积是底面积的2倍,高是3,求它的全面积.
解:
课堂小结
1.直棱柱的侧面积及表面积公式
2.正棱锥的侧面积及表面积公式
3.正棱台的侧面积及其表面积公式
4.正棱锥、正棱台斜高的求解方法
课前预习
1.直棱柱的定义________________________.
2.正棱锥的定义_____________________________________
_____________________________________.
3.正棱台的定义______________________.
4.直棱柱的侧面展开图是______;
正棱锥的侧面展开图是____________________;
正棱台的侧面展开图是____________________.
矩形
一些全等的等腰三角形
一些全等的等腰梯形
侧棱与底面垂直的棱柱
底面是正多边形,顶点在过底面中心且与底面垂直的直线上
由正棱锥截得的棱台
水立方
第一章——第一节空间几何体
1.1.6 棱柱、棱锥、棱台和球的表面积
一、直棱柱、正棱锥、正棱台的表面积
分析直六棱柱和正四棱锥的展开图
h
h
c
1.S直棱柱侧=ch
直棱柱的侧面积等于它的底面周长和高的乘积.
2.S正棱锥侧=
正棱锥的侧面积等于它的底面周长和斜高乘积的一半.
h’
斜高
a
a
正棱台的表面积
正棱台:
由正棱锥截得的棱台
分析正四棱台的展开图
3.S正棱台侧=
h’
a
a’
例1 已知正四棱锥底面边长为4,高与斜高夹角为30°,求它的侧面积和表面积.
解: 如图,正四棱锥的高为PO,
斜高为PE,底面边心距为OE,
它们组成一个直角三角形POE.
S表面积=42+32=48.
即该正四棱锥的侧面积是32,表面积是48.
变式:已知正四棱锥的斜高为4,高与斜高夹角为30°,求它的侧面积及全面积.
解:
已知正四棱台的上、下底面边长分别是2和4,高是2,求这个棱台的侧面积.
问题再探究
解:
1.已知正六棱柱的高为5 cm,最长的对角线长为13 cm,试求其侧面积.
课堂练习
解:
底面是菱形的直四棱柱中,它的对角线长为9和15,高是5,则直四棱柱的侧面积为___________
易错提示
解:
2.正四棱锥的侧面积是底面积的2倍,高是3,求它的全面积.
解:
课堂小结
1.直棱柱的侧面积及表面积公式
2.正棱锥的侧面积及表面积公式
3.正棱台的侧面积及其表面积公式
4.正棱锥、正棱台斜高的求解方法
