人教新课标B版 必修2第一章 立体几何初步 1.2 直线与平面平行的判定 19张
文档属性
| 名称 | 人教新课标B版 必修2第一章 立体几何初步 1.2 直线与平面平行的判定 19张 |

|
|
| 格式 | zip | ||
| 文件大小 | 548.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 16:53:26 | ||
图片预览





文档简介
(共19张PPT)
直线与平面平行的判定
第二课时
直线与平面平行的判定
重点:①理解并掌握直线与平面平行的判定定理;
②锻炼找平面内的直线与已知直线平行的技巧;
难点:由“线线平行”得“线面平行”,把空间问题
转化为平面问题解决的数学证明思想;
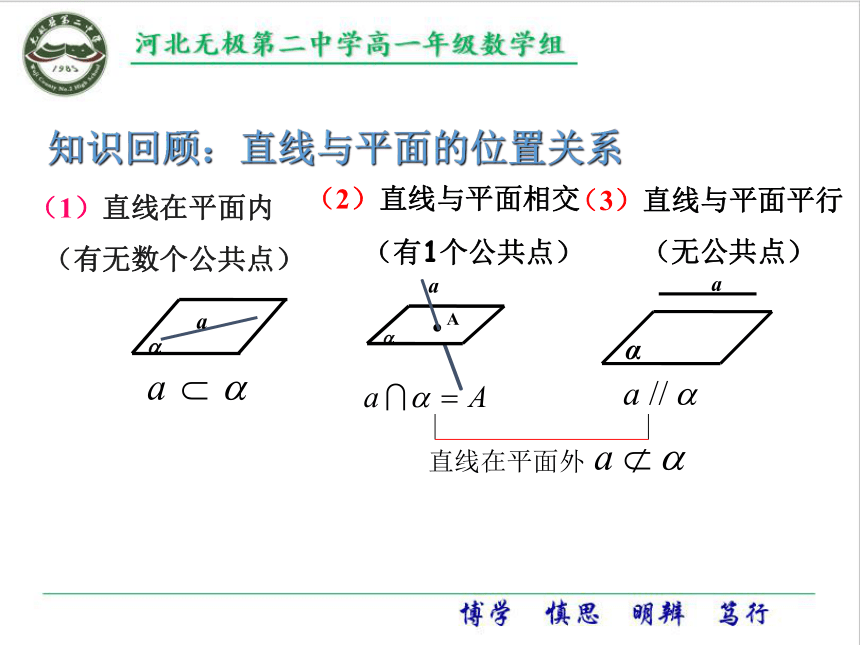
知识回顾:直线与平面的位置关系
(1)直线在平面内
(有无数个公共点)
a
(3)直线与平面平行
(无公共点)
(2)直线与平面相交
(有1个公共点)
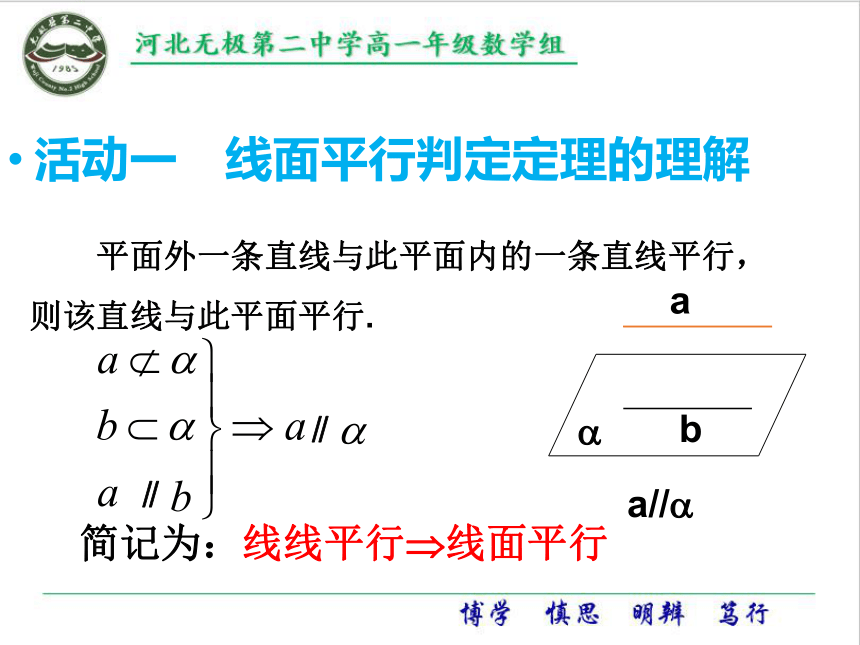
活动一 线面平行判定定理的理解
平面外一条直线与此平面内的一条直线平行,
则该直线与此平面平行.
简记为:线线平行?线面平行
练习:判断下列命题是否正确。
(1)若平面外一条直线a与直线b平行,则直线a//平面α;
(2)若平面外一直线a与平面内一条直线b平行,则直线a//平面α ;
(3)直线a在平面外,直线b在平面内α ,则直线a//平面α 。
(×)
( √ )
(×)
定理中必须的条件有三个:
a与b平行,即a∥b(平行)
注意:面外,面内,平行,三者缺一不可!
(1)定义法: 证明直线与平面无公共点;
(2)判定定理:证明平面外直线与平面内
直线平行.
怎样判定直线与平面平行?
活动二 直线与平面平行的证明
命题角度1 以锥体为背景证明线面平行
O
命题角度1 以锥体为背景证明线面平行
变式:
1.如图正方体ABCD-A1B1C1D1中,
E为DD1的中点,
证明:BD1∥平面AEC.
O
命题角度2 以柱体为背景证明线面平行
E
变式训练1
2.如图,O是长方体ABCD-A1B1C1D1
底面对角线AC与BD的交点,求证:
B1O∥平面A1C1D.
命题角度2 以柱体为背景证明线面平行
证明:如图,连接B1D1交A1C1于点O1,连接DO1,
∵B1B∥D1D,B1B=D1D,
∴四边形B1BDD1为平行四边形,
∴O1B1∥DO,O1B1=DO,
∴O1B1OD为平行四边形,
∴B1O∥O1D,
∵B1O?平面A1C1D,O1D?平面A1C1D,
∴B1O∥平面A1C1D.
1.如图,三棱柱ABC-A1B1C1中,M、 N分别是BC和A1B1的中点,求证:MN∥平面AA1C1C
活动三 小试身手
证明: 连接AN并延长交BC于P,
连接SP.
所以MN∥SP,
又MN?平面SBC,SP?平面SBC,
所以MN∥平面SBC.
1.判断或证明线面平行的常用方法
(1)定义法:证明直线与平面无公共点(不易操作).
(2)判定定理法:a?α,b?α,a∥b?a∥α.
2.证明线线平行的常用方法
(1)利用三角形中位线的性质.
(2)利用平行线分线段成比例定理.
(3)利用平行四边形的性质.
课堂小结
课后作业、预习
1、教材第61页 习题2.2 A组第3题;
2、预习:如何判定两个平面平行?
直线与平面平行的判定
第二课时
直线与平面平行的判定
重点:①理解并掌握直线与平面平行的判定定理;
②锻炼找平面内的直线与已知直线平行的技巧;
难点:由“线线平行”得“线面平行”,把空间问题
转化为平面问题解决的数学证明思想;
知识回顾:直线与平面的位置关系
(1)直线在平面内
(有无数个公共点)
a
(3)直线与平面平行
(无公共点)
(2)直线与平面相交
(有1个公共点)
活动一 线面平行判定定理的理解
平面外一条直线与此平面内的一条直线平行,
则该直线与此平面平行.
简记为:线线平行?线面平行
练习:判断下列命题是否正确。
(1)若平面外一条直线a与直线b平行,则直线a//平面α;
(2)若平面外一直线a与平面内一条直线b平行,则直线a//平面α ;
(3)直线a在平面外,直线b在平面内α ,则直线a//平面α 。
(×)
( √ )
(×)
定理中必须的条件有三个:
a与b平行,即a∥b(平行)
注意:面外,面内,平行,三者缺一不可!
(1)定义法: 证明直线与平面无公共点;
(2)判定定理:证明平面外直线与平面内
直线平行.
怎样判定直线与平面平行?
活动二 直线与平面平行的证明
命题角度1 以锥体为背景证明线面平行
O
命题角度1 以锥体为背景证明线面平行
变式:
1.如图正方体ABCD-A1B1C1D1中,
E为DD1的中点,
证明:BD1∥平面AEC.
O
命题角度2 以柱体为背景证明线面平行
E
变式训练1
2.如图,O是长方体ABCD-A1B1C1D1
底面对角线AC与BD的交点,求证:
B1O∥平面A1C1D.
命题角度2 以柱体为背景证明线面平行
证明:如图,连接B1D1交A1C1于点O1,连接DO1,
∵B1B∥D1D,B1B=D1D,
∴四边形B1BDD1为平行四边形,
∴O1B1∥DO,O1B1=DO,
∴O1B1OD为平行四边形,
∴B1O∥O1D,
∵B1O?平面A1C1D,O1D?平面A1C1D,
∴B1O∥平面A1C1D.
1.如图,三棱柱ABC-A1B1C1中,M、 N分别是BC和A1B1的中点,求证:MN∥平面AA1C1C
活动三 小试身手
证明: 连接AN并延长交BC于P,
连接SP.
所以MN∥SP,
又MN?平面SBC,SP?平面SBC,
所以MN∥平面SBC.
1.判断或证明线面平行的常用方法
(1)定义法:证明直线与平面无公共点(不易操作).
(2)判定定理法:a?α,b?α,a∥b?a∥α.
2.证明线线平行的常用方法
(1)利用三角形中位线的性质.
(2)利用平行线分线段成比例定理.
(3)利用平行四边形的性质.
课堂小结
课后作业、预习
1、教材第61页 习题2.2 A组第3题;
2、预习:如何判定两个平面平行?
