必修2 第一章 立体几何初步 1.1 空间几何体的三视图(复习课)(共27张PPT)
文档属性
| 名称 | 必修2 第一章 立体几何初步 1.1 空间几何体的三视图(复习课)(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 852.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 16:59:59 | ||
图片预览






文档简介
(共27张PPT)
空间几何体的三视图
考情分析
根据给出的三视图判定空间几何体的形状
结合几何体的表面积与体积进行计算
适用考题是选择题和填空题
重难点
课 前 热 身
1.空间几何体的三视图是指__________?__________?________. 2.三视图的排列规则是______放在正视图的下方,长度与正视图一样,________放在正视图的右面,高度与正视图一样,宽度与俯视图的宽度一样. 3.三视图的正视图?俯视图?侧视图分别是从______?______?______观察同一个几何体,画出的空间几何体的图形.
正视图
侧视图
俯视图
俯视图
侧视图
正前方
正上方
正左方
当我们从某一个角度观察一个物体时,所看到的图象叫做物体的一个视图
主视图、俯视图、左视图叫做物体的三视图
知识聚焦 双基巩固:三视图
我们用三个互相垂直 的平面(例如:墙角处的三面墙面)作为投影面
其中:正对着我们的叫正面,
正面下方的叫水平面,
右边的叫做侧面。
一个物体在三个投影面内同时进行正投影,分别:
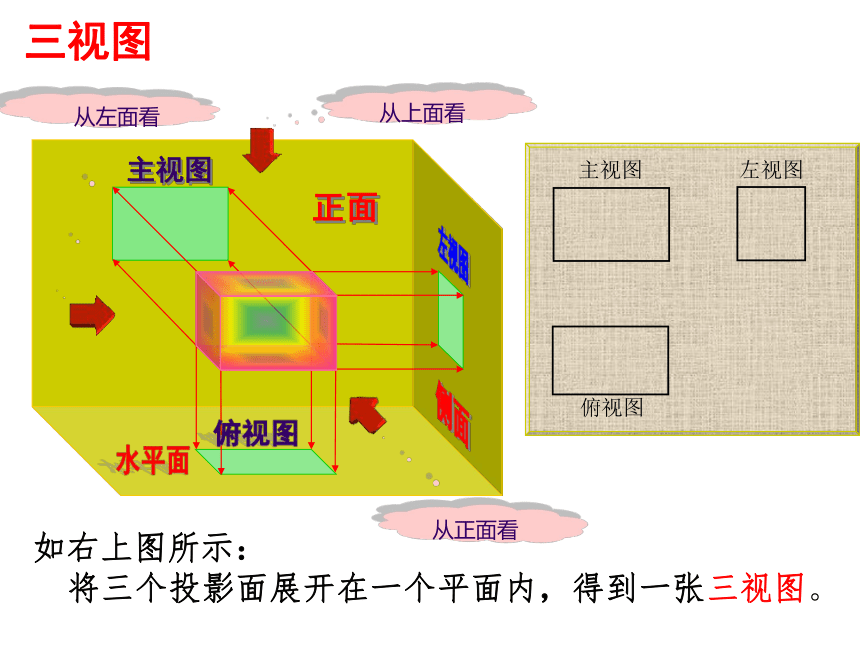
1.在正面得到的由前向后观察物体的视图,叫主视图(从前面看);
2.在水平面内得到的由上向下观察物体的视图,叫俯视图(从上面看) ;
3.在侧面内得到由左向右观察物体的视图,叫左视图(从左面看)
主视图
主视图
俯视图
左视图
正面
从上面看
从正面看
从左面看
三视图
如右上图所示:
将三个投影面展开在一个平面内,得到一张三视图。
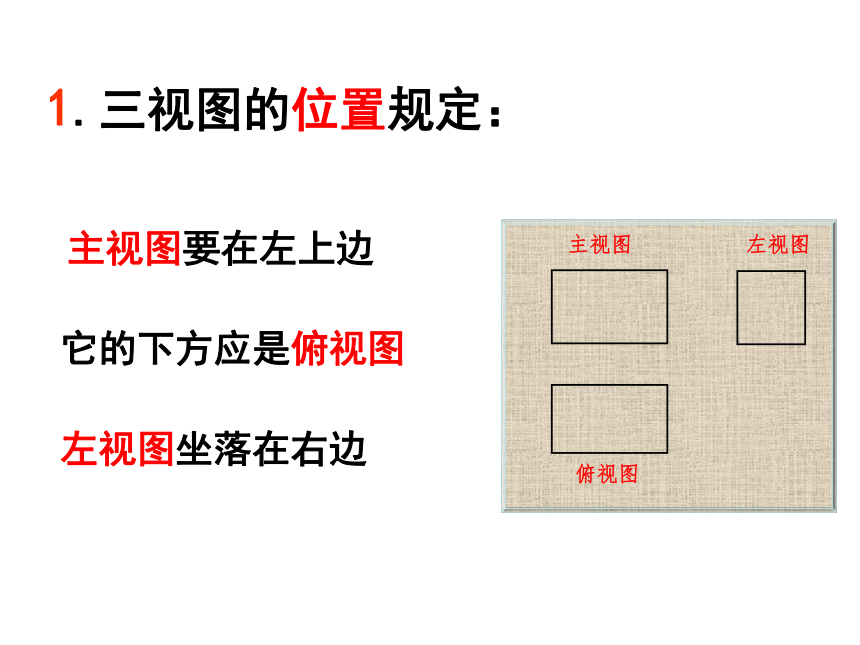
1.三视图的位置规定:
主视图
左视图
俯视图
主视图要在左上边
它的下方应是俯视图
左视图坐落在右边
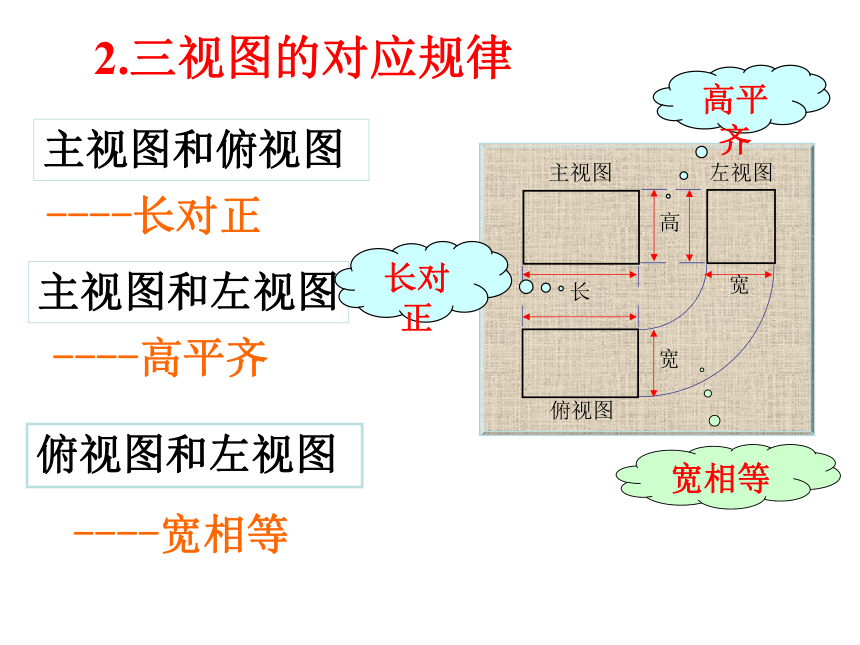
2.三视图的对应规律
俯视图和左视图
主视图和俯视图
主视图和左视图
----长对正
----高平齐
----宽相等
长对正
宽相等
高平齐
3.三视图的画法:
(1)先画主视图;
(2)在主视图正下方画出俯视图,注意与主视图“长对正”;
(3)在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”;
(4)看得见部分的轮廓线画成实线,而 看不见部分的轮廓线画成虚线.
四、简单几何的三视图
圆柱、正四棱锥和正三棱柱的三视图。
圆柱
主
侧
俯
主视图
侧视图
俯视图
正四棱锥
主
侧
俯
可见边界线都用实线画出;
不可见边界线用虚线画出;
投影面与投影方向要垂直。
【互动探究】四棱锥P-ABCD为正四棱锥,且主
视图和左视图是边长为1的正三角形,求该四棱锥的侧棱长.
【解析】如图,由条件知,正四棱锥的底边AB=1,高
则在正方形ABCD内,
故侧棱长
正三棱柱
主视图
俯视图
侧视图
主
侧
俯
正三棱锥的三视图
(a)
(b)
(c)
棱台的三视图
探索研究
三视图应用解析
一个长方体去掉一角的直观图如图所示。
关于它的三视图,画法正确的是( )
A
A.它的主视图是
B.它的主视图是
C.它的侧视图是
D.它的俯视图是
几何体投影的方法:
投影各顶点,连接。
抢答题
如图所示,将一个长方体截去一部分,这个几何体的三视图是什么?
正视
正视图
侧视图
俯视图
组内
选号
【易错误区】三视图画法中的易错点
【典例】(2012·陕西高考)将正方体(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的侧视图为( )
B
【误区警示】本题易出现的错误为实虚不分致误,不能正确区别哪些棱为可见,哪些棱为不可见,从而画错实虚线导致错误.
【规范解答】选B.图2所示的几何体的侧视图可由点A,D,D1,B1确定其外形为正方形,判断的关键是两条对角线AD1和B1C是一实一虚,且要把AD1和B1C区别开来,故选B.
2.若一个三棱柱的三视图如图所示,其俯视图为正三角形,则这个三棱柱的高和底面边长分别为 , .
答案:2 4
【解析】由三视图的画法可知,该三棱柱的高为2,底面正三角形的高为2 ,则底面边长为4.
2.一个几何体的三视图如图所示,其主视图的面积等于8,俯视
图是一个面积为 的正三角形,则其左视图的面积为( )
(A) (B) (C) (D)4
变式
【解析】选A.由三视图知该几何体是正三棱柱,设其底面边长
为a,高为h,则其主视图为矩形,矩形的面积S1=ah=8,俯视图为
边长为a的正三角形,三角形的面积
则a=4,h=2,
而左视图为矩形,底边为 高为h,故左视图的面积为
检测作业
高考总复习练习册
120页——122页的对点训练
小结说说
立体几何点线面,作图识图是关键
理解概念和定理,图形处理割补添
学会分析找思路,一作二证三计算
善于思考和勤问,回归课本才经典
空间几何体的三视图
考情分析
根据给出的三视图判定空间几何体的形状
结合几何体的表面积与体积进行计算
适用考题是选择题和填空题
重难点
课 前 热 身
1.空间几何体的三视图是指__________?__________?________. 2.三视图的排列规则是______放在正视图的下方,长度与正视图一样,________放在正视图的右面,高度与正视图一样,宽度与俯视图的宽度一样. 3.三视图的正视图?俯视图?侧视图分别是从______?______?______观察同一个几何体,画出的空间几何体的图形.
正视图
侧视图
俯视图
俯视图
侧视图
正前方
正上方
正左方
当我们从某一个角度观察一个物体时,所看到的图象叫做物体的一个视图
主视图、俯视图、左视图叫做物体的三视图
知识聚焦 双基巩固:三视图
我们用三个互相垂直 的平面(例如:墙角处的三面墙面)作为投影面
其中:正对着我们的叫正面,
正面下方的叫水平面,
右边的叫做侧面。
一个物体在三个投影面内同时进行正投影,分别:
1.在正面得到的由前向后观察物体的视图,叫主视图(从前面看);
2.在水平面内得到的由上向下观察物体的视图,叫俯视图(从上面看) ;
3.在侧面内得到由左向右观察物体的视图,叫左视图(从左面看)
主视图
主视图
俯视图
左视图
正面
从上面看
从正面看
从左面看
三视图
如右上图所示:
将三个投影面展开在一个平面内,得到一张三视图。
1.三视图的位置规定:
主视图
左视图
俯视图
主视图要在左上边
它的下方应是俯视图
左视图坐落在右边
2.三视图的对应规律
俯视图和左视图
主视图和俯视图
主视图和左视图
----长对正
----高平齐
----宽相等
长对正
宽相等
高平齐
3.三视图的画法:
(1)先画主视图;
(2)在主视图正下方画出俯视图,注意与主视图“长对正”;
(3)在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”;
(4)看得见部分的轮廓线画成实线,而 看不见部分的轮廓线画成虚线.
四、简单几何的三视图
圆柱、正四棱锥和正三棱柱的三视图。
圆柱
主
侧
俯
主视图
侧视图
俯视图
正四棱锥
主
侧
俯
可见边界线都用实线画出;
不可见边界线用虚线画出;
投影面与投影方向要垂直。
【互动探究】四棱锥P-ABCD为正四棱锥,且主
视图和左视图是边长为1的正三角形,求该四棱锥的侧棱长.
【解析】如图,由条件知,正四棱锥的底边AB=1,高
则在正方形ABCD内,
故侧棱长
正三棱柱
主视图
俯视图
侧视图
主
侧
俯
正三棱锥的三视图
(a)
(b)
(c)
棱台的三视图
探索研究
三视图应用解析
一个长方体去掉一角的直观图如图所示。
关于它的三视图,画法正确的是( )
A
A.它的主视图是
B.它的主视图是
C.它的侧视图是
D.它的俯视图是
几何体投影的方法:
投影各顶点,连接。
抢答题
如图所示,将一个长方体截去一部分,这个几何体的三视图是什么?
正视
正视图
侧视图
俯视图
组内
选号
【易错误区】三视图画法中的易错点
【典例】(2012·陕西高考)将正方体(如图1所示)截去两个三棱锥,得到图2所示的几何体,则该几何体的侧视图为( )
B
【误区警示】本题易出现的错误为实虚不分致误,不能正确区别哪些棱为可见,哪些棱为不可见,从而画错实虚线导致错误.
【规范解答】选B.图2所示的几何体的侧视图可由点A,D,D1,B1确定其外形为正方形,判断的关键是两条对角线AD1和B1C是一实一虚,且要把AD1和B1C区别开来,故选B.
2.若一个三棱柱的三视图如图所示,其俯视图为正三角形,则这个三棱柱的高和底面边长分别为 , .
答案:2 4
【解析】由三视图的画法可知,该三棱柱的高为2,底面正三角形的高为2 ,则底面边长为4.
2.一个几何体的三视图如图所示,其主视图的面积等于8,俯视
图是一个面积为 的正三角形,则其左视图的面积为( )
(A) (B) (C) (D)4
变式
【解析】选A.由三视图知该几何体是正三棱柱,设其底面边长
为a,高为h,则其主视图为矩形,矩形的面积S1=ah=8,俯视图为
边长为a的正三角形,三角形的面积
则a=4,h=2,
而左视图为矩形,底边为 高为h,故左视图的面积为
检测作业
高考总复习练习册
120页——122页的对点训练
小结说说
立体几何点线面,作图识图是关键
理解概念和定理,图形处理割补添
学会分析找思路,一作二证三计算
善于思考和勤问,回归课本才经典
