人教新课标B版必修2第一章 立体几何初步1.2.2直线与平面平行的性质定理 18张
文档属性
| 名称 | 人教新课标B版必修2第一章 立体几何初步1.2.2直线与平面平行的性质定理 18张 |

|
|
| 格式 | zip | ||
| 文件大小 | 522.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
直线和平面平行的性质
*
1.直线与平面平行的判定定理是什么?
定理 若平面外一条直线与此平面内的
一条直线平行,则该直线与此平面平行.
2.直线与平面平行的判定定理解决了直线与平面平行的条件问题,反之,在直线与平面平行的条件下,可以得到什么结论呢?
复习回顾
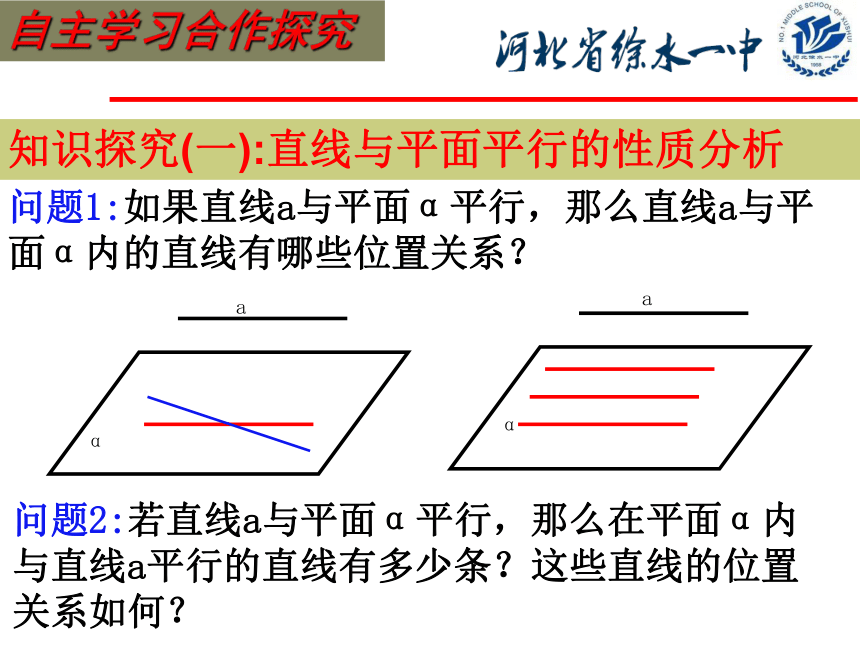
问题1:如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?
问题2:若直线a与平面α平行,那么在平面α内与直线a平行的直线有多少条?这些直线的位置关系如何?
知识探究(一):直线与平面平行的性质分析
自主学习合作探究
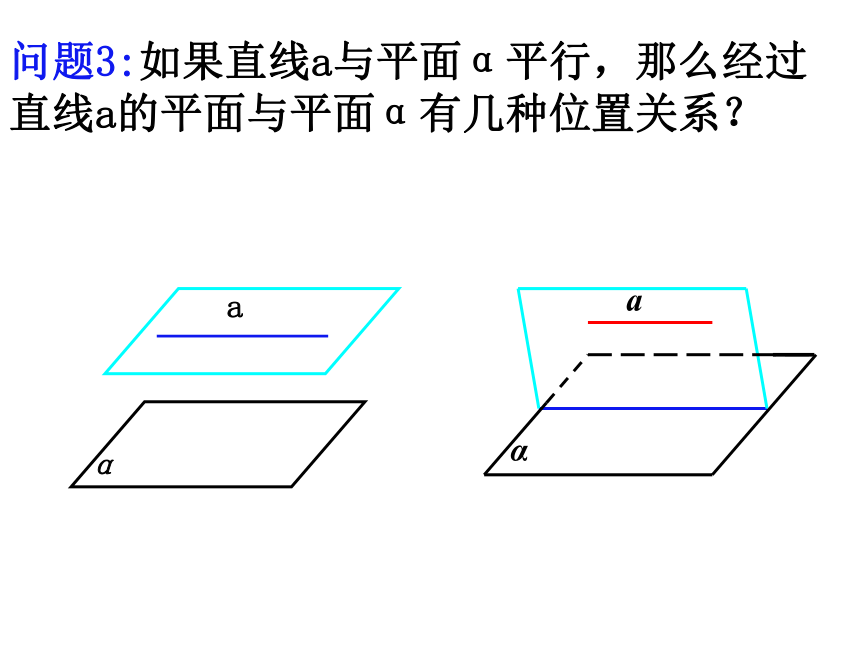
问题3:如果直线a与平面α平行,那么经过直线a的平面与平面α有几种位置关系?
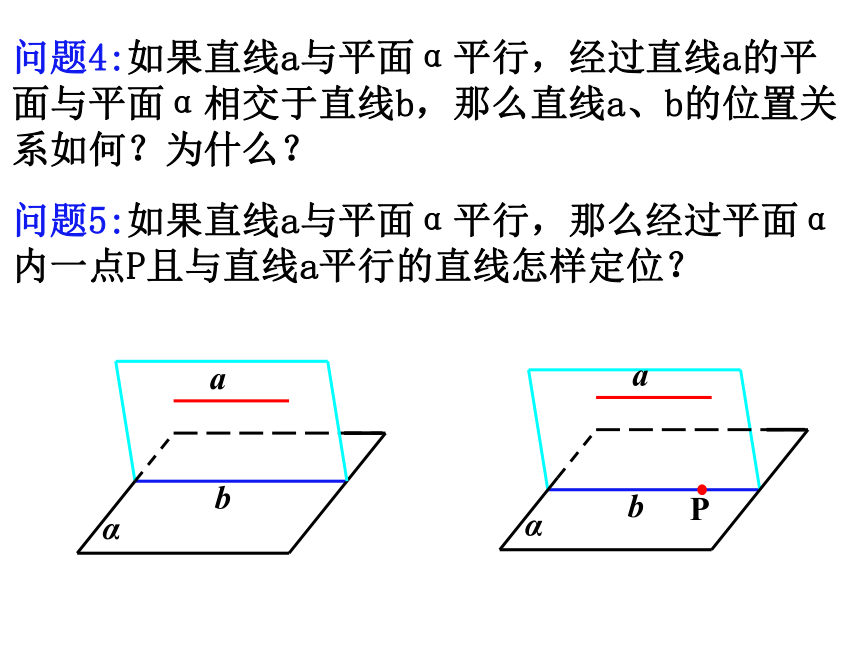
问题4:如果直线a与平面α平行,经过直线a的平面与平面α相交于直线b,那么直线a、b的位置关系如何?为什么?
问题5:如果直线a与平面α平行,那么经过平面α内一点P且与直线a平行的直线怎样定位?
知识探究(二):直线与平面平行的性质定理
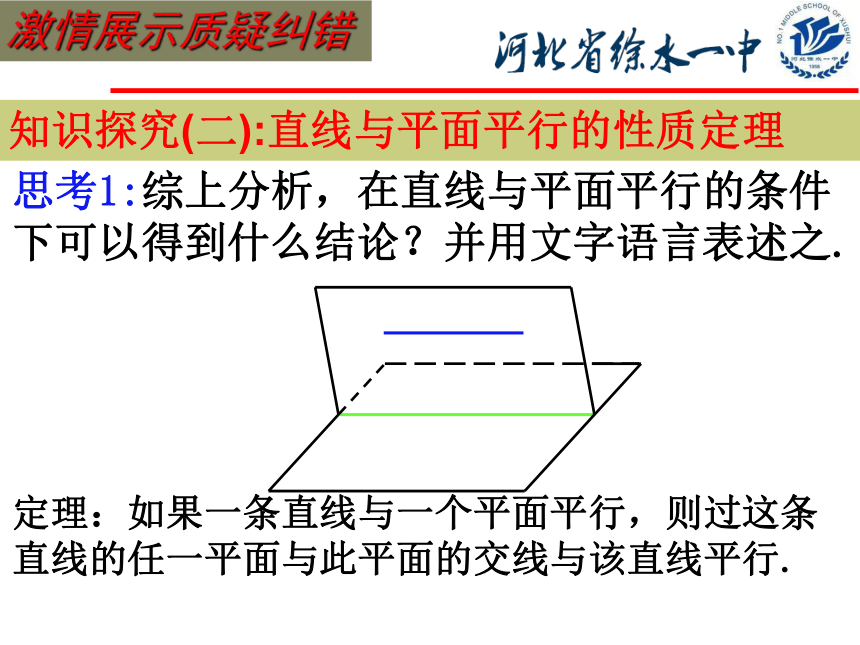
思考1:综上分析,在直线与平面平行的条件
下可以得到什么结论?并用文字语言表述之.
定理:如果一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.
激情展示质疑纠错
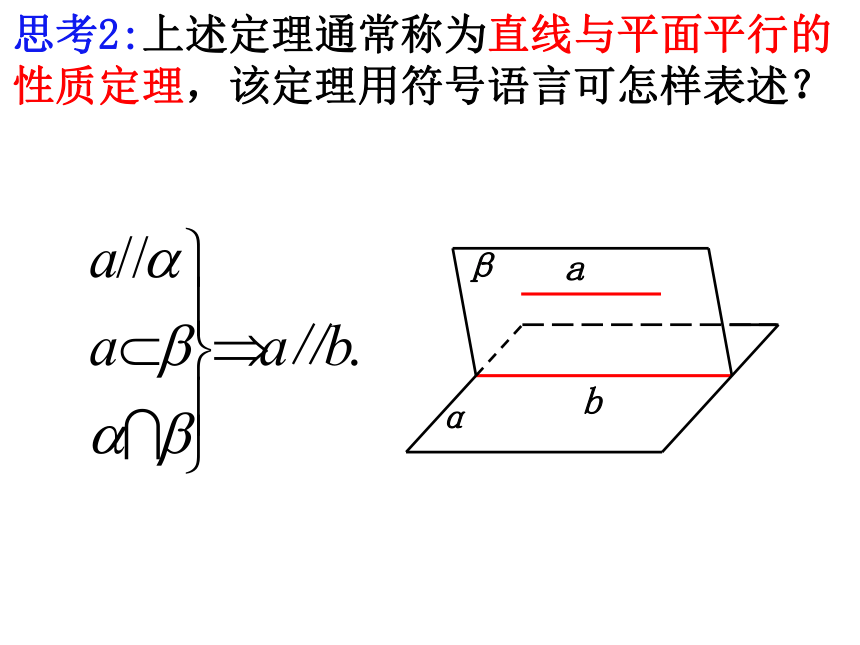
思考2:上述定理通常称为直线与平面平行的性质定理,该定理用符号语言可怎样表述?
思考3:直线与平面平行的性质定理可简述为“线面平行,则线线平行”,在实际应用中它有何功能作用?
作平行线的方法,判断线线平行的依据.
例1. 如图所示的一块木料中,棱BC平行于面A'C'.
过点P作直EF//B'C',
棱A'B'、C'D'于点E、F,
连结BE、CF,
F
P
E
解:
⑴如图,
在平面A'C'内,
下面证明EF、BE、
CF为应画的线.
分别交
⑴要经过面A'C'内的一点P和棱BC 将木料锯开,应怎样画线?
精讲点拨总结升华
⑴
则EF、BE、CF为应画的线.
BC//B'C'
EF//B'C'
BC//EF
EF、BE、CF共面.
例1. 如图所示的一块木料中,棱BC平行于面A'C'.
解:
F
P
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
例1. 如图所示的一块木料中,棱BC平行于面A'C'.
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
⑵
解:
EF//面AC
由⑴,得
BE、CF都与面相交.
EF//BC,
EF//BC
线面平行
线线平行
线面平行
例2 .求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.
α
β
l
b
c
已知:α∩β=l,a∥α,a∥β.
求证:a∥l.
2.本节课你学会了哪些数学思想方法?
1.本节课你学会了哪些知识?
课堂总结
练习1:已知正方体ABCD—A1B1C1D1的棱长为1,
点P是面AA1D1D的中心,点Q是B1D1上一点,
C1
D1
且PQ//面AB1,则线段 PQ长为 .
达标测试拓展延伸
A
B
C
D
A1
B1
P
Q
练习2:已知平面外的两条平行直线中的一条平行于这个平面,求证另一条也平行于这个平面.
如图,已知直线a,b和平面α ,a∥b, a∥α , a,b都在平面α外 .求证:b∥α .
练习3:ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面 BDM于GH.
求证:AP//GH
P
A
B
C
D
M
G
H
O
课后作业
作业:固学案直线与平面平行限时练
直线和平面平行的性质
*
1.直线与平面平行的判定定理是什么?
定理 若平面外一条直线与此平面内的
一条直线平行,则该直线与此平面平行.
2.直线与平面平行的判定定理解决了直线与平面平行的条件问题,反之,在直线与平面平行的条件下,可以得到什么结论呢?
复习回顾
问题1:如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?
问题2:若直线a与平面α平行,那么在平面α内与直线a平行的直线有多少条?这些直线的位置关系如何?
知识探究(一):直线与平面平行的性质分析
自主学习合作探究
问题3:如果直线a与平面α平行,那么经过直线a的平面与平面α有几种位置关系?
问题4:如果直线a与平面α平行,经过直线a的平面与平面α相交于直线b,那么直线a、b的位置关系如何?为什么?
问题5:如果直线a与平面α平行,那么经过平面α内一点P且与直线a平行的直线怎样定位?
知识探究(二):直线与平面平行的性质定理
思考1:综上分析,在直线与平面平行的条件
下可以得到什么结论?并用文字语言表述之.
定理:如果一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.
激情展示质疑纠错
思考2:上述定理通常称为直线与平面平行的性质定理,该定理用符号语言可怎样表述?
思考3:直线与平面平行的性质定理可简述为“线面平行,则线线平行”,在实际应用中它有何功能作用?
作平行线的方法,判断线线平行的依据.
例1. 如图所示的一块木料中,棱BC平行于面A'C'.
过点P作直EF//B'C',
棱A'B'、C'D'于点E、F,
连结BE、CF,
F
P
E
解:
⑴如图,
在平面A'C'内,
下面证明EF、BE、
CF为应画的线.
分别交
⑴要经过面A'C'内的一点P和棱BC 将木料锯开,应怎样画线?
精讲点拨总结升华
⑴
则EF、BE、CF为应画的线.
BC//B'C'
EF//B'C'
BC//EF
EF、BE、CF共面.
例1. 如图所示的一块木料中,棱BC平行于面A'C'.
解:
F
P
E
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
例1. 如图所示的一块木料中,棱BC平行于面A'C'.
⑴要经过面内的一点P和棱BC将木料锯开,应
怎样画线?
⑵所画的线与平面AC是什么位置关系?
⑵
解:
EF//面AC
由⑴,得
BE、CF都与面相交.
EF//BC,
EF//BC
线面平行
线线平行
线面平行
例2 .求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.
α
β
l
b
c
已知:α∩β=l,a∥α,a∥β.
求证:a∥l.
2.本节课你学会了哪些数学思想方法?
1.本节课你学会了哪些知识?
课堂总结
练习1:已知正方体ABCD—A1B1C1D1的棱长为1,
点P是面AA1D1D的中心,点Q是B1D1上一点,
C1
D1
且PQ//面AB1,则线段 PQ长为 .
达标测试拓展延伸
A
B
C
D
A1
B1
P
Q
练习2:已知平面外的两条平行直线中的一条平行于这个平面,求证另一条也平行于这个平面.
如图,已知直线a,b和平面α ,a∥b, a∥α , a,b都在平面α外 .求证:b∥α .
练习3:ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面 BDM于GH.
求证:AP//GH
P
A
B
C
D
M
G
H
O
课后作业
作业:固学案直线与平面平行限时练
