1.2.2直线与平面平行的判定定理(共26张PPT)
文档属性
| 名称 | 1.2.2直线与平面平行的判定定理(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 545.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
a
2.2 直线与平面平行的判定
在空间中,直线与平面有几种位置关系?
一、复习回顾
直线与平面有几种位置关系?
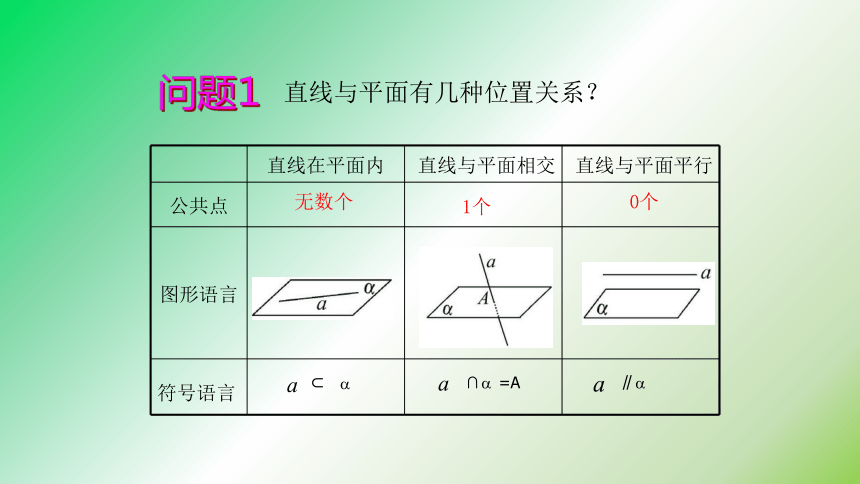
问题1
直线在平面内 直线与平面相交 直线与平面平行
公共点
图形语言
符号语言
1个
0个
无数个
∥?
?
?
∩ =A
?
在日常生活中,哪些实例给我们以直线与平面平行的印象呢?
二、实例感知
实例感受
将一本书平放在桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?
在生活中,注意到门扇的两边是平行的.当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇转动的一边与门框所在的平面给人以平行的印象.
实例感受
怎样判定直线与平面平行呢?
1、根据定义 直线和平面没有公共点
2、给你一条直线和一个平面,如何能保证直线和平面没有公共点?
三、动手探究 抽象概括
将平行四边形,矩形,梯形,三角形中相互平行的其中一条边放到桌面内,观察另一边所在的直线与桌面的位置关系?
(一)动手探究
我要探究
寻找“参照物”
A
B
C
D
A
B
C
D
A
B
C
D
S
A
B
C
D
平行四边形
矩形
梯形
三角形中位线
若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
(二)抽象概括
(三)存惑解疑
是否可以保证一定平行吗?
(1)这两条直线共面吗?
(2)直线a与平面 相交吗?
若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
定理
三、 动手探究 抽象概括
我要探究
文字语言
图形语言
符号语言
直线与平面平行的判定
定理
若平面外一条直线与此平面内的
一条直线平行,则该直线与此平面平行.
注意隐藏的
数学思想方法.
∵ ?? , b ? ? ,
∥b
∴ ∥?
线(平面外)线(平面内)平行 线面平行
化归
直线与平面平行(空间)
直线平行(平面)
四、实践应用
a
b
c
d
例1.如图,四棱柱ABCD— A1B1C1D1 中,
AA1 ( ) 平面BB1C1C
A、⊥ B、 ∥ C、 ∈ D、 .
五 定理运用 形成技能
C1
A1
B1
D1
B
与直线 A A1 平行的平面有 ( )个.
A、4 B、 3 C、 2 D、 1 .
C
心得:
看看平面
内有没有一条现
成的线与AA1平行.
变变又如何
例2 求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面.
已知:空间四边形ABCD中,E,F分别是AB,AD的中点.
求证:EF//平面BCD.
证明:连接BD.
因为 AE=EB,
AF=FD,
因为
EF//平面BCD.
.
.
所以 EF // BD
分析: (1)文字证明题应先依题意画出图形
然后写出已知、求证,最后写出证明过程 。
(2)注意空间四边形的画法。
心得:
利用中位线的平行性是常用手段之一.
如何在平面内找一条线与
EF 平行是关键.
典型例题
已知:空间四边形ABCD中,
E,F分别AB,AD的中点.
求证:EF//平面BCD.
.
.
证明:连接BD.
因为 AE=EB,
AF=FD,
因为
EF//平面BCD.
所以 EF // BD
E,F分别是AB,AD上的点,且
变式
对应线段成比例也是证明
线线平行的常用方法.
1.如图,长方体 中,
(1)与AB平行的平面是 ;
(2)与 平行的平面是 ;
(3)与AD平行的平面是 ;
平面
平面
平面
平面
平面
平面
随堂练习
∵ O为正方形DBCE 对角线的交点,
∴ BO=OE,
又AF=FE,
∴AB//OF,
B
D
F
O
2.如图,四棱锥A—DBCE中,
O为底面正方形DBCE对角线
的交点, F为AE的中点.
求证: OF//平面ABD.
证明:
A
C
E
?
ABD
AB
平面
ABD
OF
平面
?
∴ OF//平面ABD
随堂练习
O
C1
B1
A1
D1
E
A
B
C
D
证明:
连接BD交AC于点O, 连接OE,
在正方形ABCD中,O是BD的中点
∵E 为 的中点
∴ EO∥BD1
BD1
BD1
随堂练习
∴AE//GF, AE=GF,
A
D
F
4. 如图,四棱锥P—ABCD中,底面ABCD是平行四边形,
E、F分别是AB、PC的中点.
求证: EF//平面PAD.
证明: 作PD的中点G, 连接AG, GF
P
B
C
E
G
∵ PG=GD, PF=FC,
∴GF ∥ DC,
又∵ ABCD是平行四边形,
E是AB的中点
∴AE∥ DC,
∴AEFG是平行四边形
∴EF∥ AG
∴ EF//平面PAD
画线面平行时,怎样画图更直观
地体现线面平行 ?
常使已知直线与平面内的某条直线平行
探究题
能谈谈你的收获吗?
一、直线与平面平行的判定定理
二、证明直线与平面平行的方法
三、运用判定定理时的几个要点
四、运用定理的关键:找平行线
六、收获感悟 总结提高
五、立体几何的基本思想:化归
谢 谢!
a
2.2 直线与平面平行的判定
在空间中,直线与平面有几种位置关系?
一、复习回顾
直线与平面有几种位置关系?
问题1
直线在平面内 直线与平面相交 直线与平面平行
公共点
图形语言
符号语言
1个
0个
无数个
∥?
?
?
∩ =A
?
在日常生活中,哪些实例给我们以直线与平面平行的印象呢?
二、实例感知
实例感受
将一本书平放在桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?
在生活中,注意到门扇的两边是平行的.当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇转动的一边与门框所在的平面给人以平行的印象.
实例感受
怎样判定直线与平面平行呢?
1、根据定义 直线和平面没有公共点
2、给你一条直线和一个平面,如何能保证直线和平面没有公共点?
三、动手探究 抽象概括
将平行四边形,矩形,梯形,三角形中相互平行的其中一条边放到桌面内,观察另一边所在的直线与桌面的位置关系?
(一)动手探究
我要探究
寻找“参照物”
A
B
C
D
A
B
C
D
A
B
C
D
S
A
B
C
D
平行四边形
矩形
梯形
三角形中位线
若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
(二)抽象概括
(三)存惑解疑
是否可以保证一定平行吗?
(1)这两条直线共面吗?
(2)直线a与平面 相交吗?
若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.
定理
三、 动手探究 抽象概括
我要探究
文字语言
图形语言
符号语言
直线与平面平行的判定
定理
若平面外一条直线与此平面内的
一条直线平行,则该直线与此平面平行.
注意隐藏的
数学思想方法.
∵ ?? , b ? ? ,
∥b
∴ ∥?
线(平面外)线(平面内)平行 线面平行
化归
直线与平面平行(空间)
直线平行(平面)
四、实践应用
a
b
c
d
例1.如图,四棱柱ABCD— A1B1C1D1 中,
AA1 ( ) 平面BB1C1C
A、⊥ B、 ∥ C、 ∈ D、 .
五 定理运用 形成技能
C1
A1
B1
D1
B
与直线 A A1 平行的平面有 ( )个.
A、4 B、 3 C、 2 D、 1 .
C
心得:
看看平面
内有没有一条现
成的线与AA1平行.
变变又如何
例2 求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面.
已知:空间四边形ABCD中,E,F分别是AB,AD的中点.
求证:EF//平面BCD.
证明:连接BD.
因为 AE=EB,
AF=FD,
因为
EF//平面BCD.
.
.
所以 EF // BD
分析: (1)文字证明题应先依题意画出图形
然后写出已知、求证,最后写出证明过程 。
(2)注意空间四边形的画法。
心得:
利用中位线的平行性是常用手段之一.
如何在平面内找一条线与
EF 平行是关键.
典型例题
已知:空间四边形ABCD中,
E,F分别AB,AD的中点.
求证:EF//平面BCD.
.
.
证明:连接BD.
因为 AE=EB,
AF=FD,
因为
EF//平面BCD.
所以 EF // BD
E,F分别是AB,AD上的点,且
变式
对应线段成比例也是证明
线线平行的常用方法.
1.如图,长方体 中,
(1)与AB平行的平面是 ;
(2)与 平行的平面是 ;
(3)与AD平行的平面是 ;
平面
平面
平面
平面
平面
平面
随堂练习
∵ O为正方形DBCE 对角线的交点,
∴ BO=OE,
又AF=FE,
∴AB//OF,
B
D
F
O
2.如图,四棱锥A—DBCE中,
O为底面正方形DBCE对角线
的交点, F为AE的中点.
求证: OF//平面ABD.
证明:
A
C
E
?
ABD
AB
平面
ABD
OF
平面
?
∴ OF//平面ABD
随堂练习
O
C1
B1
A1
D1
E
A
B
C
D
证明:
连接BD交AC于点O, 连接OE,
在正方形ABCD中,O是BD的中点
∵E 为 的中点
∴ EO∥BD1
BD1
BD1
随堂练习
∴AE//GF, AE=GF,
A
D
F
4. 如图,四棱锥P—ABCD中,底面ABCD是平行四边形,
E、F分别是AB、PC的中点.
求证: EF//平面PAD.
证明: 作PD的中点G, 连接AG, GF
P
B
C
E
G
∵ PG=GD, PF=FC,
∴GF ∥ DC,
又∵ ABCD是平行四边形,
E是AB的中点
∴AE∥ DC,
∴AEFG是平行四边形
∴EF∥ AG
∴ EF//平面PAD
画线面平行时,怎样画图更直观
地体现线面平行 ?
常使已知直线与平面内的某条直线平行
探究题
能谈谈你的收获吗?
一、直线与平面平行的判定定理
二、证明直线与平面平行的方法
三、运用判定定理时的几个要点
四、运用定理的关键:找平行线
六、收获感悟 总结提高
五、立体几何的基本思想:化归
谢 谢!
