1.2.2 空间中的平行关系 课件(共29张PPT)
文档属性
| 名称 | 1.2.2 空间中的平行关系 课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 17:59:23 | ||
图片预览



文档简介
(共29张PPT)
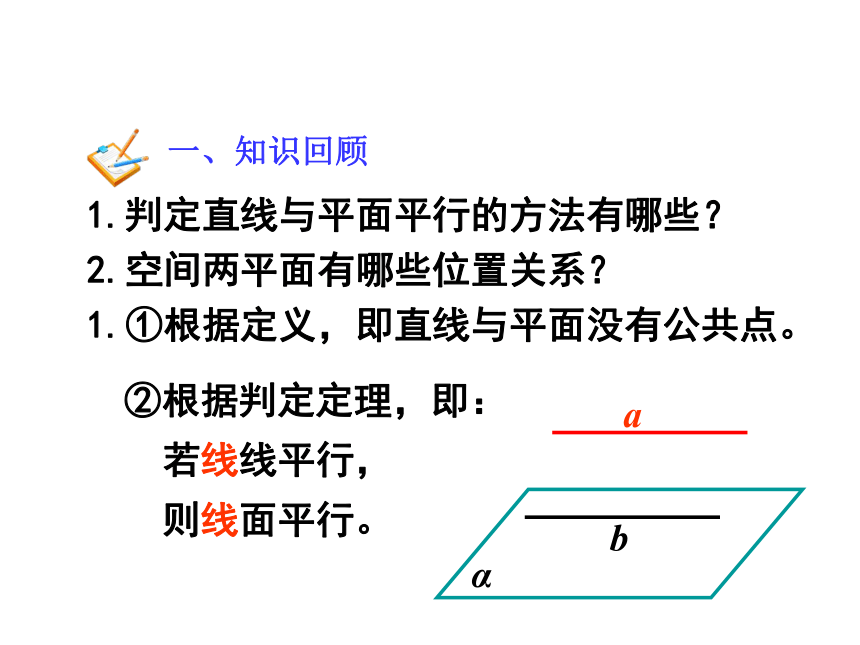
平面与平面平行的判定
②根据判定定理,即:
若线线平行,
则线面平行。
一、知识回顾
2.空间两平面有哪些位置关系?
1.判定直线与平面平行的方法有哪些?
a
b
α
1.①根据定义,即直线与平面没有公共点。
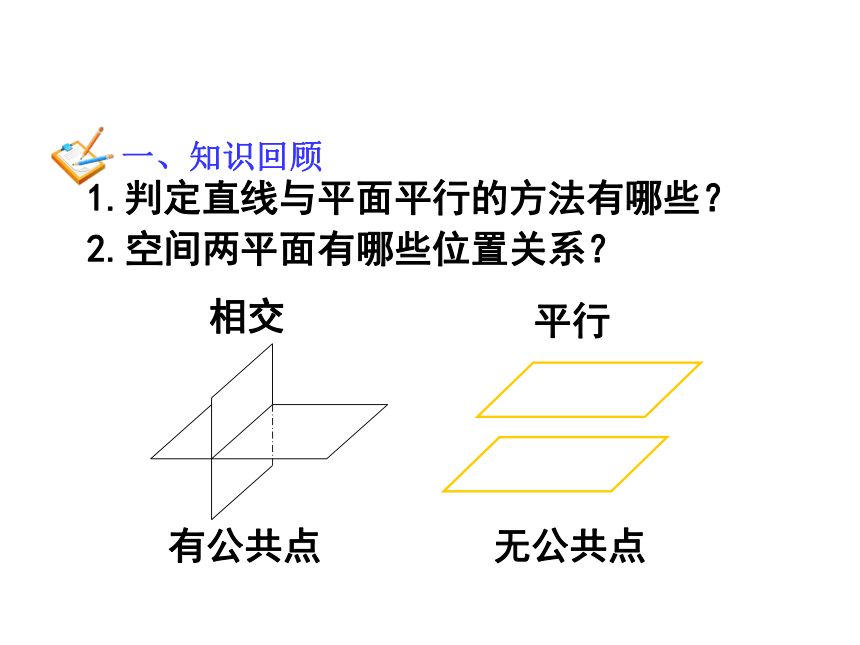
一、知识回顾
2.空间两平面有哪些位置关系?
1.判定直线与平面平行的方法有哪些?
相交
平行
有公共点
无公共点
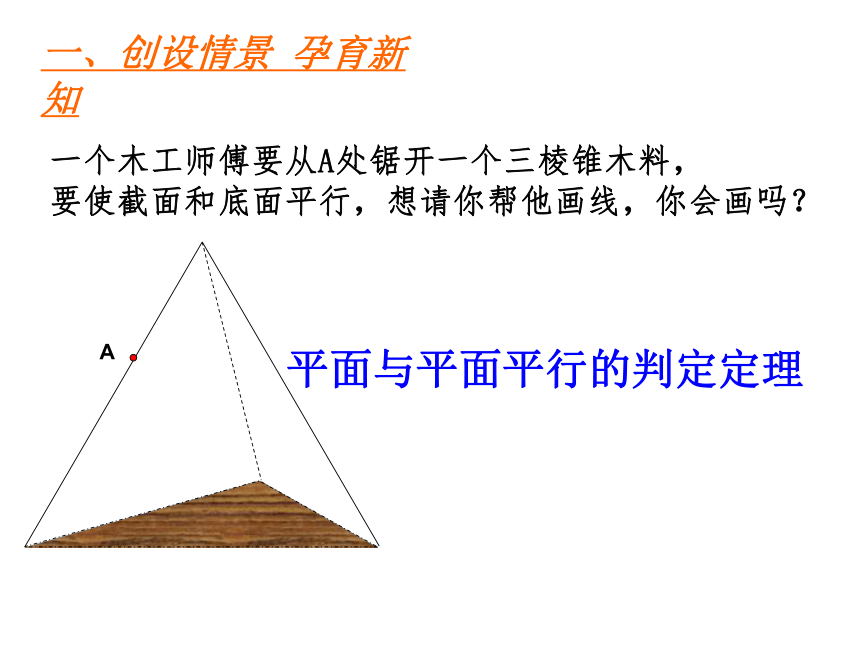
一个木工师傅要从A处锯开一个三棱锥木料,
要使截面和底面平行,想请你帮他画线,你会画吗?
一、创设情景 孕育新知
平面与平面平行的判定定理
判定方法1:定义法
如果两平面没有公共点,那么两平面平行
实质:其中一个平面内任何一条直线都平行于另一平面
平面与平面平行的判定方法
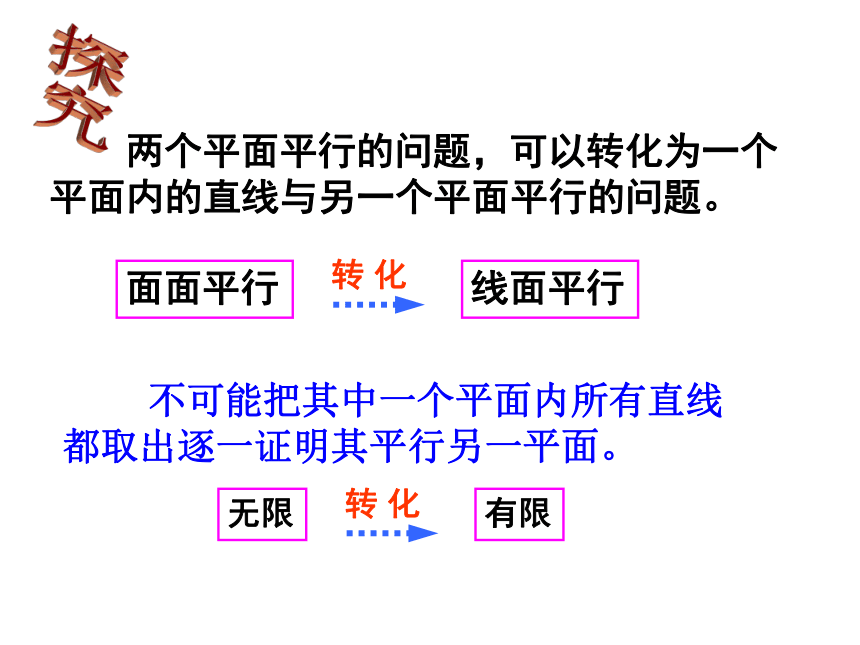
二、师生协助 探索新知
两个平面平行的问题,可以转化为一个平面内的直线与另一个平面平行的问题。
不可能把其中一个平面内所有直线都取出逐一证明其平行另一平面。
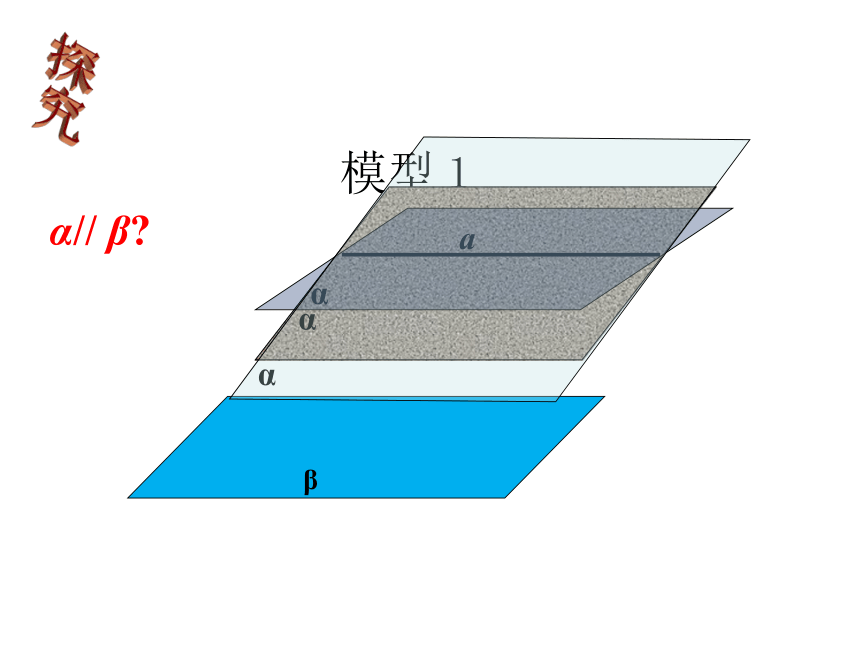
1、平面α内有一条直线与平面β平行,平面α,β一定平行吗?
模型1
α
β
α// β?
α
α
1、平面α内有一条直线与平面β平行,平面α,β一定平行吗?
(不一定)
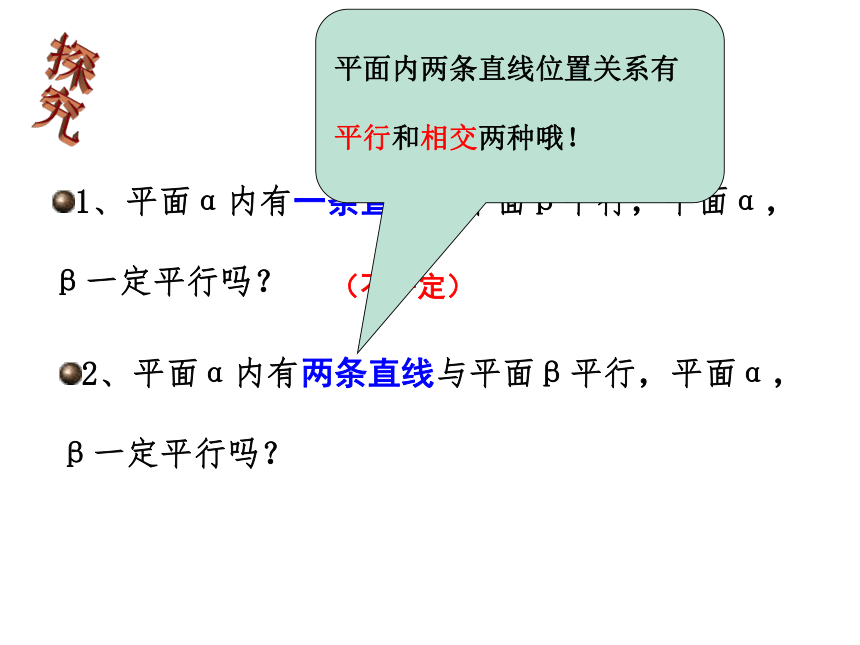
2、平面α内有两条直线与平面β平行,平面α,β一定平行吗?
平面内两条直线位置关系有平行和相交两种哦!
一平面内两条平行直线都平行于另一平面
两平面位置关系?
直观
感受
平面α内有两条相交直线 a , b 平行平面β, 则α∥ β吗?
模型
验证
平面α内有两条相交直线 a , b 平行平面β, 则α∥ β吗?
你能得到什么结论
1、平面α内有一条直线与平面β平行,平面α,β一定平行吗?
(不一定)
2、平面α内有两条直线与平面β平行,平面α,β一定平行吗?
两平行直线 (不一定)
两相交直线 ( ?)
a ?? , b??
a?b=P
a // ?
b // ?
?// ?
面面平行的判定定理
符号语言
线不在多
贵在相交
面面平行
线面平行
线线平行?
a
b
?
图形语言
?
?
如果一个 有两条 直线分别
于另一个平面
相交
,那么这两个平面平行。
P
平面内
平行
三、探索新知,形成概念
a ?? , b??
a?b=P
a // ?
b // ?
?// ?
面面平行的判定定理
符号语言
线不在多
贵在相交
a
b
?
图形语言
?
?
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
P
面面平行
线面平行
线线平行?
1.线面平行是否可用其它条件代替?
a ?? , b??
a?b=P
a // ?
b // ?
?// ?
面面平行的判定定理
a
b
?
?
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
可用什么
条件代替?
变式探究
?
线面平行
线线平行?
a ?? , b??
a?b=P
b // ?
?// ?
a
b
?
?
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
1.线面平行是否可用其它条件代替?
变式探究
?
线面平行
线线平行?
a ?? , b??
a?b=P
b // ?
?// ?
a
b
图形语言
?
?
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
.线面平行是否可用其它条件代替?
变式探究
符号语言
?
线面平行
线线平行?
a ?? , b??
a?b=P
?// ?
a
b
图形语言
?
?
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
,那么这两个平面平行。
内的两直线
.线面平行是否可用其它条件代替?
变式探究
推论
符号语言
?
四、定理的理解:
例.(课本练习第1题)判断下列命题是否正确,正确的说明理由,错误的举例说明:
(1)已知平面 和直线 ,
若 ,则
(2)一个平面 内两条不平行的直线都平行于另一平面 ,则
错误
正确
D
1
D
C
B
A
C
1
B
1
A
1
(课本57页例 2): 已知正方体ABCD-A1B1C1D1
求证:平面AB1D1∥平面C1BD.
变式一:已知正方体ABCD-A1B1C1D1(如图),
P, Q, R分别为A1A, A1B1, A1D1 的中点,
求证:平面PQR∥平面C1BD.
R
Q
P
五、合作交流 运用新知
变式:已知正方体ABCD-A1B1C1D1(如图),
P, Q, R分别为A1A, A1B1, A1D1 的中点
求证:平面PQR∥平面C1BD.
D
1
R
Q
D
C
B
A
C
1
B
1
A
1
P
(课本57页例 2): 已知正方体ABCD-A1B1C1D1
求证:平面AB1D1∥平面C1BD.
五、合作交流 运用新知
第一步:在一个平面内找出两条相交直线;
第二步:证明两条相交直线分别平行于另一个平面。
第三步:利用判定定理得出结论。
面面平行
3、证明面面平行书写的三个条件“内”、“交”、 “平行”, 缺一不可。
1、证明两个平面平行的基本思路:
2、证明两个平面平行的一般步骤:
六、方法总结
一个木匠师傅要从A处锯开一个三棱锥木料,
要使截面和底面平行,想请你帮他画线,你会画吗?
七、运用新知 解决问题
一个木匠师傅要从A处锯开一个三棱锥木料,
要使截面和底面平行,想请你帮他画线,你会画吗?
七、运用新知 解决问题
七、运用新知 解决问题
2.应用判定定理判定面面平行时应注意:
1.平面与平面平行的判定:
3.应用判定定理判定面面平行的关键是找平行线
证明面面平行的书写三个条件“内”、“交”、“平行”,缺一不可。
4.数学思想方法:转化的思想
平面和平面没有公共点
面面平行
转化
线面平行
转化
线线平行
空间问题
平面问题
转化
八、课堂收获
1、定义法:
2、面面平行的判定定理:
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
教材P62练习:7,8
九、课外作业
巩固练习
例 1: 判断下列结论是否正确:
1.若m?α, n?α, m∥β, n∥β, 则α∥β
2.若α内有无数条直线平行于β, 则α∥β
3.若α内任意直线都平行于β, 则α∥β
4.若m // n,m//α,m //β,n//α,n//β,则α//β
5.若α//γ,β//γ,则α//β
平面与平面平行的判定
②根据判定定理,即:
若线线平行,
则线面平行。
一、知识回顾
2.空间两平面有哪些位置关系?
1.判定直线与平面平行的方法有哪些?
a
b
α
1.①根据定义,即直线与平面没有公共点。
一、知识回顾
2.空间两平面有哪些位置关系?
1.判定直线与平面平行的方法有哪些?
相交
平行
有公共点
无公共点
一个木工师傅要从A处锯开一个三棱锥木料,
要使截面和底面平行,想请你帮他画线,你会画吗?
一、创设情景 孕育新知
平面与平面平行的判定定理
判定方法1:定义法
如果两平面没有公共点,那么两平面平行
实质:其中一个平面内任何一条直线都平行于另一平面
平面与平面平行的判定方法
二、师生协助 探索新知
两个平面平行的问题,可以转化为一个平面内的直线与另一个平面平行的问题。
不可能把其中一个平面内所有直线都取出逐一证明其平行另一平面。
1、平面α内有一条直线与平面β平行,平面α,β一定平行吗?
模型1
α
β
α// β?
α
α
1、平面α内有一条直线与平面β平行,平面α,β一定平行吗?
(不一定)
2、平面α内有两条直线与平面β平行,平面α,β一定平行吗?
平面内两条直线位置关系有平行和相交两种哦!
一平面内两条平行直线都平行于另一平面
两平面位置关系?
直观
感受
平面α内有两条相交直线 a , b 平行平面β, 则α∥ β吗?
模型
验证
平面α内有两条相交直线 a , b 平行平面β, 则α∥ β吗?
你能得到什么结论
1、平面α内有一条直线与平面β平行,平面α,β一定平行吗?
(不一定)
2、平面α内有两条直线与平面β平行,平面α,β一定平行吗?
两平行直线 (不一定)
两相交直线 ( ?)
a ?? , b??
a?b=P
a // ?
b // ?
?// ?
面面平行的判定定理
符号语言
线不在多
贵在相交
面面平行
线面平行
线线平行?
a
b
?
图形语言
?
?
如果一个 有两条 直线分别
于另一个平面
相交
,那么这两个平面平行。
P
平面内
平行
三、探索新知,形成概念
a ?? , b??
a?b=P
a // ?
b // ?
?// ?
面面平行的判定定理
符号语言
线不在多
贵在相交
a
b
?
图形语言
?
?
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
P
面面平行
线面平行
线线平行?
1.线面平行是否可用其它条件代替?
a ?? , b??
a?b=P
a // ?
b // ?
?// ?
面面平行的判定定理
a
b
?
?
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
可用什么
条件代替?
变式探究
?
线面平行
线线平行?
a ?? , b??
a?b=P
b // ?
?// ?
a
b
?
?
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
1.线面平行是否可用其它条件代替?
变式探究
?
线面平行
线线平行?
a ?? , b??
a?b=P
b // ?
?// ?
a
b
图形语言
?
?
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
.线面平行是否可用其它条件代替?
变式探究
符号语言
?
线面平行
线线平行?
a ?? , b??
a?b=P
?// ?
a
b
图形语言
?
?
如果一个平面内有两条 直线分别
平行于另一个平面
相交
,那么这两个平面平行。
,那么这两个平面平行。
内的两直线
.线面平行是否可用其它条件代替?
变式探究
推论
符号语言
?
四、定理的理解:
例.(课本练习第1题)判断下列命题是否正确,正确的说明理由,错误的举例说明:
(1)已知平面 和直线 ,
若 ,则
(2)一个平面 内两条不平行的直线都平行于另一平面 ,则
错误
正确
D
1
D
C
B
A
C
1
B
1
A
1
(课本57页例 2): 已知正方体ABCD-A1B1C1D1
求证:平面AB1D1∥平面C1BD.
变式一:已知正方体ABCD-A1B1C1D1(如图),
P, Q, R分别为A1A, A1B1, A1D1 的中点,
求证:平面PQR∥平面C1BD.
R
Q
P
五、合作交流 运用新知
变式:已知正方体ABCD-A1B1C1D1(如图),
P, Q, R分别为A1A, A1B1, A1D1 的中点
求证:平面PQR∥平面C1BD.
D
1
R
Q
D
C
B
A
C
1
B
1
A
1
P
(课本57页例 2): 已知正方体ABCD-A1B1C1D1
求证:平面AB1D1∥平面C1BD.
五、合作交流 运用新知
第一步:在一个平面内找出两条相交直线;
第二步:证明两条相交直线分别平行于另一个平面。
第三步:利用判定定理得出结论。
面面平行
3、证明面面平行书写的三个条件“内”、“交”、 “平行”, 缺一不可。
1、证明两个平面平行的基本思路:
2、证明两个平面平行的一般步骤:
六、方法总结
一个木匠师傅要从A处锯开一个三棱锥木料,
要使截面和底面平行,想请你帮他画线,你会画吗?
七、运用新知 解决问题
一个木匠师傅要从A处锯开一个三棱锥木料,
要使截面和底面平行,想请你帮他画线,你会画吗?
七、运用新知 解决问题
七、运用新知 解决问题
2.应用判定定理判定面面平行时应注意:
1.平面与平面平行的判定:
3.应用判定定理判定面面平行的关键是找平行线
证明面面平行的书写三个条件“内”、“交”、“平行”,缺一不可。
4.数学思想方法:转化的思想
平面和平面没有公共点
面面平行
转化
线面平行
转化
线线平行
空间问题
平面问题
转化
八、课堂收获
1、定义法:
2、面面平行的判定定理:
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
教材P62练习:7,8
九、课外作业
巩固练习
例 1: 判断下列结论是否正确:
1.若m?α, n?α, m∥β, n∥β, 则α∥β
2.若α内有无数条直线平行于β, 则α∥β
3.若α内任意直线都平行于β, 则α∥β
4.若m // n,m//α,m //β,n//α,n//β,则α//β
5.若α//γ,β//γ,则α//β
