人教版高中数学必修三知识讲解,巩固练习(教学资料,补习资料):专题3.2 古典概型
文档属性
| 名称 | 人教版高中数学必修三知识讲解,巩固练习(教学资料,补习资料):专题3.2 古典概型 |

|
|
| 格式 | zip | ||
| 文件大小 | 513.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-26 08:16:00 | ||
图片预览




文档简介
第三章 概率
3.2古典概型
知识
1.古典概型
(1)基本事件
在一次试验中,可能出现的每一个基本结果叫做基本事件.
基本事件有如下特点:
①任何两个基本事件是___________的.
②任何事件(除不可能事件)都可以表示成___________.
(2)古典概型
把具有特点:①试验中所有可能出现的基本事件只有___________个;②每个基本事件出现的可能性___________的概率模型称为古典概率模型,简称古典概型.
2.古典概型的概率公式
如果一次试验中,可能出现的结果有个,而且所有结果出现的可能性相等,那么每一个基本事件的概率都是;如果事件包含的基本事件有个,那么事件的概率为_______=_________.
3.(整数值)随机数的产生
(1)随机数与伪随机数
例如我们要产生1~25之间的随机整数,我们把25个大小形状相同的小球分别标上1,2,3,…,24,25,放入一个袋中,把它们充分搅拌,然后从中摸出一个,这个球上的数就称为随机数.
计算机或计算器产生的随机数是依照确定算法产生的数,具有周期性(周期很长),它们具有类似随机数的性质.因此,计算机或计算器产生的并不是真正的随机数,我们称它们为伪随机数.
(2)随机数的产生方法
课本中给出了两种产生随机数的方法:①利用带有PRB功能的计算器产生随机数;②用计算机软件产生随机数,比如用Excel软件产生随机数.
(3)用随机模拟方法估计概率
用计算机或计算器模拟试验的方法称为随机模拟方法或蒙特卡罗方法.
其基本步骤是:①建立概率模型;②进行模拟试验,可用计算器或计算机进行模拟试验;③统计试验的结果.
知识参考答案:
1.(1)①互斥 ②基本事件的和 (2)①有限 ②相等
2.
重点
重点
理解古典概型的概念及利用古典概型求解随机事件的概率
难点
判断一个试验是否是古典概型,分清在一个古典概型中某随机事件包含的基本事件的个数和试验中基本事件的总数
易错
利用古典概型的概率公式求解时,要注意试验的每个基本事件是等可能发生的
1.古典概型的判定
并不是所有的试验都是古典概型,只有同时满足有限性和等可能性这两个条件的试验才是古典概型.两个条件中只要有一个不满足就不是古典概型.
【例1】(1)在数轴上0~3之间任取一点x,观察x是否小于1.此试验是否为古典概型?为什么?
(2)从1,2,3,4四个数中任意取出两个数,观察所取两数之一是否是5.此试验是古典概型吗?试说明理由.
(3)投掷一颗质地非均匀的骰子,观察掷出的点数.此试验是否为古典概型?为什么?
【解析】(1)在数轴上0~3之间任取一点,此点可以在0~3之间的任一位置,且在每个位置上的可能性是相同的,具备等可能性.但试验结果有无限多个,不满足古典概型试验结果的有限性.因此不属于古典概型.
(2)此试验是古典概型,因为此试验的所有基本事件共有6个:(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),且每个事件的出现是等可能的,因此属于古典概型.
(3)投掷一颗质地非均匀的骰子,掷出的点数不是等可能出现的,质地较重的那一面朝下的可能性比较大,其对面的点数出现的可能性就比其他点数出现的可能性大,因此不属于古典概型.
2.古典概型的计算
求古典概型的概率的关键是正确列出基本事件,在写出基本事件后最好检验一下各基本事件发生的概率是否相同.求随机事件的概率的关键就是明晰它包含了几个基本事件.
要写出所有的基本事件可采用的方法较多,例如列举法、列表法、坐标系法、树形图法等.无论采用哪种方法,都要求按照一定的顺序进行,以做到不重不漏.
【例2】某中学调查了某班全部名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团
未参加书法社团
参加演讲社团
未参加演讲社团
(1)从该班随机选名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的名同学中,有5名男同学名女同学现从这名男同学和名女同学中各随机选人,求被选中且未被选中的概率.
【解析】(1)由调查数据可知,既未参加书法社团又未参加演讲社团的有人,
故至少参加上述一个社团的共有人,
所以从该班随机选名同学,该同学至少参加上述一个社团的概率为
(2)从这名男同学和名女同学中各随机选人,其一切可能的结果组成的基本事件有:
,共个.
根据题意,这些基本事件的出现是等可能的.
事件“被选中且未被选中”所包含的基本事件有:,共个.
因此被选中且未被选中的概率为.
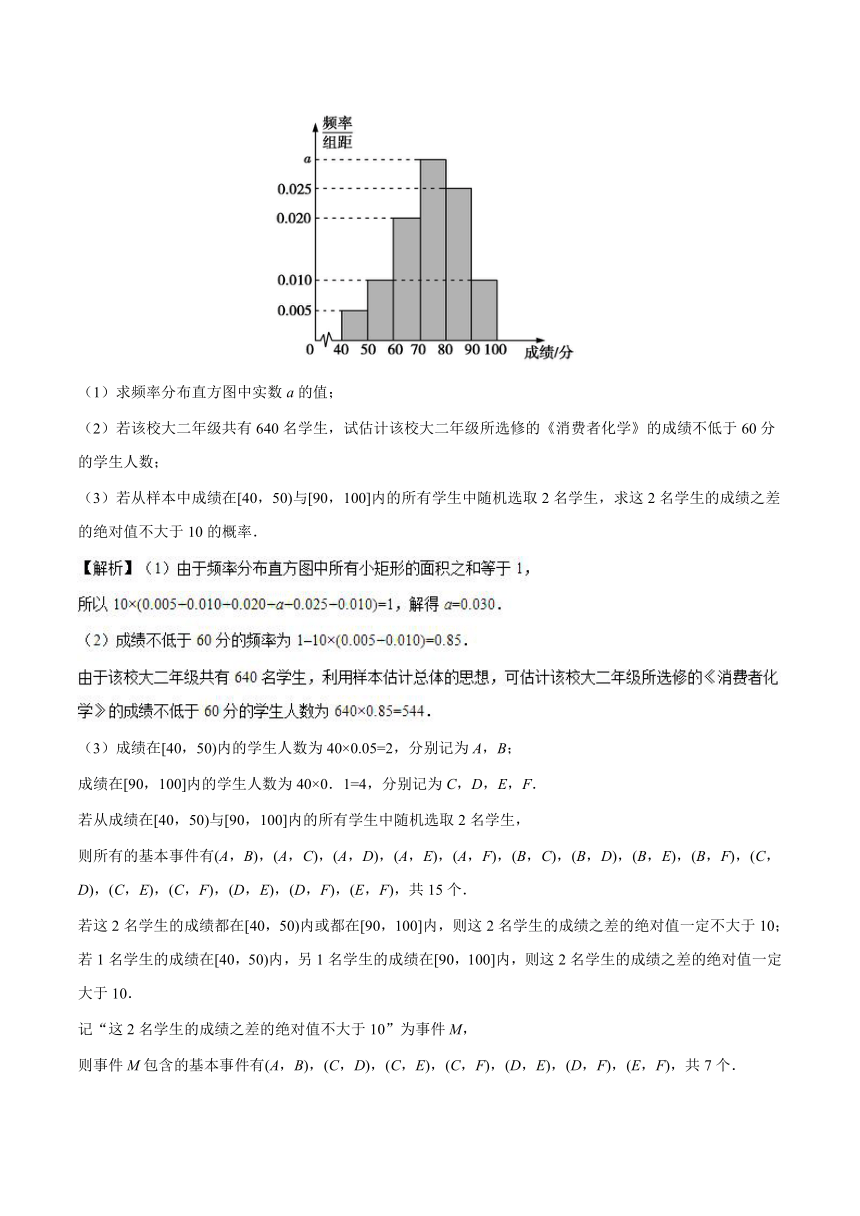
【例3】某大学的教授从大二年级学生所选修的《消费者化学》的成绩中随机抽取40名学生的成绩,分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.
(1)求频率分布直方图中实数a的值;
(2)若该校大二年级共有640名学生,试估计该校大二年级所选修的《消费者化学》的成绩不低于60分的学生人数;
(3)若从样本中成绩在[40,50)与[90,100]内的所有学生中随机选取2名学生,求这2名学生的成绩之差的绝对值不大于10的概率.
(3)成绩在[40,50)内的学生人数为40×0.05=2,分别记为A,B;
成绩在[90,100]内的学生人数为40×0.1=4,分别记为C,D,E,F.
若从成绩在[40,50)与[90,100]内的所有学生中随机选取2名学生,
则所有的基本事件有(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15个.
若这2名学生的成绩都在[40,50)内或都在[90,100]内,则这2名学生的成绩之差的绝对值一定不大于10;若1名学生的成绩在[40,50)内,另1名学生的成绩在[90,100]内,则这2名学生的成绩之差的绝对值一定大于10.
记“这2名学生的成绩之差的绝对值不大于10”为事件M,
则事件M包含的基本事件有(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共7个.
所以所求的概率为P(M)=.
【名师点睛】概率问题常与统计问题综合考查,在此类问题中,注意灵活运用概率与统计的知识求解.
3.用随机模拟估计概率
用随机模拟估计概率的关键是用相应的整数表示试验的结果,然后按实际需要将所得的随机数分为若干个一组(比如试验要求随机抽取三个球就三个数据一组),明晰所求事件的特点后去找符合要求的数据组,即可求解概率.
【例4】已知某运动员每次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中;5,6,7,8,9,0表示不命中,再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
137 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为
A.0.40 B.0.30
C.0.35 D.0.25
【答案】B
【解析】由题意,得在20组模拟数据中,表示该运动员三次投篮恰有两次命中的数据有:137、191、271、932、812、393,共6个数据,故该运动员三次投篮恰有两次命中的概率为.故选B.
4.混淆“等可能”与“非等可能”
【例5】从5名男生和3名女生中任选1人去参加演讲比赛,求选中女生的概率.
【错解】从8人中选出1人的结果有“男生”“女生”两种,则选中女生的概率为.
【错因分析】因为男生人数多于女生人数,所以选中男生的机会大于选中女生的机会,它们不是等可能的.
【正解】选出1人的所有可能的结果有8种,即共有8个基本事件,其中选中女生的基本事件有3个,故选中女生的概率为.
【名师点睛】利用古典概型的概率公式求解时,注意需满足两个条件:
(1)所有的基本事件只有有限个;
(2)试验的每个基本事件是等可能发生的.
基础训练
1.下列有关古典概型的四种说法:
①试验中所有可能出现的基本事件只有有限个;
②每个事件出现的可能性相等;
③每个基本事件出现的可能性相等;
④已知基本事件总数为n,若随机事件A包含k个基本事件,则事件A发生的概率P(A)=.
其中所有正确说法的序号是
A.①②④ B.①③ C.③④ D.①③④
2.盒中有2个红色的变形金刚,2个白色的变形金刚,2个黑色的变形金刚,从里面任意取2个变形金刚,不是基本事件的为
A.{恰好2个红色的变形金刚} B.{恰好2个黑色的变形金刚}
C.{恰好2个白色的变形金刚} D.{至少1个红色的变形金刚}
3.下列试验是古典概型的是
A.在适宜的条件下,种下一粒种子,观察它是否发芽
B.口袋里有2个白球和2个黑球,这4个球除颜色外完全相同,从中任取一球
C.向一个圆面内随机投一点
D.射击运动员向一靶心进行射击,试验结果为命中10环,命中9环,……,命中0环
4.把一枚骰子投掷两次,观察出现的点数,记第一次出现的点数为a,第二次出现的点数为b,则方程组只有一组解的概率为
A. B. C. D.
5.从甲、乙等5名学生中随机选出2名,则甲被选中的概率为
A. B. C. D.
6.甲、乙两人一起去游览公园,他们约定各自独立地从1号到6号景点中任选4个进行游览,每个景点参观1小时,则最后一小时他们在同一个景点的概率是
A. B. C. D.
7.在平面直角坐标系中,从下列5个点:A(0,0),B(2,0),C(1,1),D(0,2),E(2,2)中任取3个,这三点能构成三角形的概率是
A. B. C. D.1
能力提升
8.某天放学以后,教室里还剩下2位男同学和2位女同学.若他们依次走出教室,则第2位走出的是男同学的概率是
A. B. C. D.
9.某大学餐饮中心为了解新生的饮食习惯,在全校大一学生中进行了抽样调查.已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,则至多有1人喜欢甜品的概率为
A.0.3 B.0.4 C.0.6 D.0.7
10.某城市有连接8个小区A,B,C,D,E,F,G,H和市中心O的整齐方格形道路网,每个小方格均为正方形,如图所示.某人从道路网中随机地选择一条最短路径,由小区A前往小区H,则他经过市中心O的概率为
A. B. C. D.
11.现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率.先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 0293 7140 9857 0347
4373 8636 6947 1417 4698
0371 6233 2616 8045 6011
3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为
A.0.852 B.0.819 2 C.0.8 D.0.75
12.从正六边形的6个顶点中随机选出4个,以它们作为顶点的四边形是矩形的概率为____________.
13.一个口袋内装有1个白球和编号分别为1,2,3的3个黑球,它们的大小、质地相同,从中任意摸出2个球.
(1)共有多少个基本事件?每个基本事件是否等可能出现?该试验是古典概型吗?
(2)“摸出的2个球都是黑球”记为事件A,则事件A包含哪几个基本事件?
14.甲、乙两名运动员为了争夺某比赛最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.
(1)根据茎叶图分析甲、乙两名运动员中谁的比赛成绩更稳定?
(2)若从甲运动员的7轮比赛中任选3个不低于80且不高于90的得分,求这3个得分与其7轮比赛的平均得分的差的绝对值都不超过2的概率.
15.小陈以游戏方式决定是参加学校合唱团还是参加学校足球队.游戏规则:从A1,A2,A3,A4,A5,A6(如图)这6个点中任取2个点,记选取的在y轴上的点的个数为X.若X=0就参加学校合唱团,否则就参加学校足球队.
(1) 请列出从A1,A2,A3,A4,A5,A6中任取2个点的所有可能情况;
(2)求小陈不参加学校合唱团的概率.
16.一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外,其他完全相同.现随机有放回地抽取3次,每次抽取一张,将抽取的卡片上的数字依次记为a,b,C.
(1)求“抽取的卡片上的数字满足a+b=c”的概率;
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
17.从含有两件正品a1,a2和一件次品b1的三件产品中每次任取一件,连续取两次.
(1)若每次取出后不放回,求取出的两件产品中恰有一件次品的概率;
(2)若每次取出后放回,求取出的两件产品中恰有一件次品的概率.
18.从一批草莓中随机抽取n个,其质量(单位:g)的频数分布表如下:
分组
[80,85)
[85,90)
[90,95)
[95,100)
频数
10
50
x
15
已知从这n个草莓中随机抽取1个,其质量在[90,95)内的概率为.
(1)求n,x的值;
(2)用分层抽样的方法从质量在[80,85)和[95,100)内的草莓中抽取5个,再从这5个草莓中任取2个,求质量在[80,85)和[95,100)内各有1个的概率.
19.福建某网络营销部门随机抽查了福州市200名网友在2017年“双十一”的网购金额,所得数据如下:
网购金额/千元
人数
频率
(0,1]
16
0.08
(1,2]
24
0.12
(2,3]
x
p
(3,4]
y
q
(4,5]
16
0.08
(5,6]
14
0.07
合计
200
1.00
已知网购金额不超过3千元与超过3千元的人数之比恰为3∶2.
(1)试确定x,y,p,q的值,并补全频率分布直方图;
(2)该营销部门为了了解该市网友的购物体验,从这200名网友中,用分层抽样的方法从网购金额在(1,2]和(4,5]的两个群体中抽取5人进行问卷调查,若需从这5人中随机选取2人继续访谈,求这2人来自不同群体的概率.
真题练习
20.(2018?全国)甲、乙、丙、丁、戊站成一排,甲不在两端的概率
A. B. C. D.
21.(2018?新课标Ⅱ)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是
A. B. C. D.
22.(2019?天津模拟)有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为
A. B. C. D.
23.(2017?新课标Ⅱ)从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
A. B. C. D.
24.(2019?山东模拟)从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,每次抽取1张,则抽到在2张卡片上的数奇偶性不同的概率是
A. B. C. D.
25.(2018?上海)有编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,从中随机选取三个,则这三个砝码的总质量为9克的概率是____________(结果用最简分数表示).
26.(2019?江苏模拟)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为____________.
27.(2017?上海)已知四个函数:①y=–x,②y=–,③y=x3,④y=x,从中任选2个,则事件“所选2个函数的图象有且仅有一个公共点”的概率为__________.
28.(2019?天津模拟)己知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.
29.(2019?山东文科模拟)某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率.
30.(2017?全国卷Ⅲ文)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:°C)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温
[10,15)
[15,20)
[20,25)
[25,30)
[30,35)
[35,40)
天数
2
16
36
25
7
4
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
参考答案
1
2
3
4
5
6
7
8
9
10
11
20
21
22
23
24
D
D
B
B
B
D
C
A
D
B
D
B
C
C
D
C
1.【答案】D
【解析】②中所说的事件不一定是基本事件,所以②不正确;根据古典概型的特点及计算公式可知①③④正确.故选D.
2.【答案】D
【解析】至少1个红色的变形金刚包含1红1白或1红1黑或2红,所以{至少1个红色的变形金刚}不是基本事件,其他项中的事件都是基本事件.故选D.
5.【答案】B
【解析】设这5名学生分别是甲、乙、丙、丁、戊,从中随机选出2名的方法有(甲,乙),(甲,丙),(甲,丁),(甲,戊),(乙,丙),(乙,丁),(乙,戊),(丙,丁),(丙,戊),(丁,戊),共有10种,其中甲被选中有4种,所以所求概率为=.
6.【答案】D
【解析】甲、乙最后一小时所在的景点共有36种情况,甲、乙最后一小时在同一个景点共有6种情况.由古典概型的概率公式,知后一小时他们在同一个景点的概率是=.
7.【答案】C
【解析】从5个点中任取3个点,有ABC,ABD,ABE,ACD,ACE,ADE,BCD,BCE,BDE,CDE,共10个基本事件,其中ACE,BCD 2个事件中的点不能构成三角形,故能构成三角形的概率为=.
8.【答案】A
【解析】2位男同学和2位女同学走出教室的所有可能顺序有(女,女,男,男),(女,男,女,男),(女,男,男,女),(男,男,女,女),(男,女,男,女),(男,女,女,男),共6种,所以第2位走出的是男同学的概率是P==,故选A.
9.【答案】D
【解析】记2名喜欢甜品的学生分别为a1,a2,3名不喜欢甜品的学生分别为b1,b2,b3.从5名数学系学生中任取3人的所有可能结果组成的基本事件有10个,分别为{a1,a2,b1},{a1,a2,b2},{a1,a2,b3},{a1,b1,b2},{a1,b1,b3},{a1,b2,b3},{a2,b1,b2},{a2,b1,b3},{a2,b2,b3},{b1,b2,b3}.记事件A表示“至多有1人喜欢甜品”,则事件A所包含的基本事件分别为{a1,b1,b2},{a1,b1,b3},{a1,b2,b3},{a2,b1,b2},{a2,b1,b3},{a2,b2,b3},{b1,b2,b3},共7个.根据古典概型的概率计算公式,得至多有1人喜欢甜品的概率P(A)==0.7,故选D.
10.【答案】B
【解析】由题意,知此人从小区A前往小区H的所有最短路径为A→B→C→E→H,A→B→O→E→H,A→B→O→G→H,A→D→O→E→H,A→D→O→G→H,A→D→F→G→H,共6条.记“此人经过市中心O”为事件M,则M包含的基本事件为A→B→O→E→H,A→B→O→G→H,A→D→O→E→H,A→D→O→G→H,共4条,所以P(M)==,即他经过市中心O的概率为.
13.【答案】(1)每个基本事件是等可能出现的,这个试验是古典概型;(2)详见解析.
【解析】(1)任意摸出2个球,共有
(白,黑1),(白,黑2),(白,黑3),(黑1,黑2),(黑1,黑3),(黑2,黑3),
共6个基本事件,且每个基本事件是等可能出现的,这个试验是古典概型.
(2)事件A包含(黑1,黑2),(黑1,黑3),(黑2,黑3),共3个基本事件.
14.【答案】(1)乙运动员的比赛成绩更稳定;(2).
【解析】(1)由茎叶图,可知甲、乙两名运动员7轮比赛的得分情况为
甲:78,81,84,85,84,85,91;乙:79,84,84,86,87,84,91.
所以甲运动员的平均得分=84,方差=,
乙运动员的平均得分=85,方差=,
由于>,故乙运动员的比赛成绩更稳定.
(2)由(1)知,甲运动员的7轮比赛得分中不低于80且不高于90的得分共有5个,
分别是81,84,85,84,85.
从中任选的3个得分记为(x,y,z),则不同的结果有
(81,84,85),(81,84,84),(81,84,85),(81,85,84),(81,85,85),
(81,84,85),(84,85,84),(84,85,85),(84,84,85),(85,84,85),共10种,
这3个得分与其7轮比赛的平均得分的差的绝对值都不超过2的情况有
(84,85,84),(84,85,85),(84,84,85),(85,84,85),共4种.
所以所求的概率P==.
15.【答案】(1)详见解析;(2).
【解析】(1)从A1,A2,A3,A4,A5,A6中任取2个点包含的所有情况为
{A1,A2},{A1,A3},{A1,A4},{A1,A5},{A1,A6},
{A2,A3},{A2,A4},{A2,A5},{A2,A6},
{A3,A4},{A3,A5},{A3,A6},{A4,A5},{A4,A6},{A5,A6},共有15种.
(2)当X=0时,所取的2个点均不在y轴上,即从A1,A2,A5,A6中任取2个点,
所有可能的情况为{A1,A2},{A1,A5},{A1,A6},{A2,A5},{A2,A6},{A5,A6},共6种,
所以小陈参加学校合唱团的概率为=,
所以小陈不参加学校合唱团的概率P=1–=.
16.【答案】(1).(2).
【解析】(1)由题意,(a,b,c)所有可能的结果为
(1,1,1),(1,1,2),(1,1,3),(1,2,1),(1,2,2),(1,2,3),
(1,3,1),(1,3,2),(1,3,3),(2,1,1),(2,1,2),(2,1,3),
(2,2,1),(2,2,2),(2,2,3),(2,3,1),(2,3,2),(2,3,3),
(3,1,1),(3,1,2),(3,1,3),(3,2,1),(3,2,2),(3,2,3),
(3,3,1),(3,3,2),(3,3,3),共27种.
设“抽取的卡片上的数字满足a+b=c”为事件A,则事件A包括
(1,1,2),(1,2,3),(2,1,3),共3种,所以P(A)==.
因此,“抽取的卡片上的数字满足a+b=c”的概率为.
(2)设“抽取的卡片上的数字a,b,c不完全相同”为事件B,则事件包括
(1,1,1),(2,2,2),(3,3,3),共3种,
所以P(B)=1–P()=1–=,
因此,“抽取的卡片上的数字a,b,c不完全相同”的概率为.
17.【答案】(1).(2).
【解析】(1)不放回地连续取两次,其基本事件为
(a1,a2),(a1,b1),(a2,a1),(a2,b1),(b1,a1),(b1,a2),共 6个.
记“取出的两件产品中恰有一件次品”为事件A,
则事件A由(a1,b1),(a2,b1),(b1,a1),(b1,a2)这4个基本事件组成,
因而P(A)==.
(2)有放回地连续取两次,其基本事件为
(a1,a1),(a1,a2),(a1,b1),(a2,a1),(a2,a2),(a2,b1),
(b1,a1),(b1,a2),(b1,b1),共9个.
记“取出的两件产品中恰有一件次品”为事件B,
则事件B由(a1,b1),(a2,b1),(b1,a1),(b1,a2)这4个基本事件组成,
因而P(B)=.
18.【答案】(1)x=20,n=95.(2).
【解析】(1)依题意可得,解得x=20,n=95.
(2)若采用分层抽样的方法从质量在[80,85)和[95,100)内的草莓中抽取5个,
则质量在[80,85)内的个数为×5=2,记为x,y,
在[95,100)内的个数为×5=3,记为a,b,c.
从抽出的5个草莓中,任取2个,有
(x,a),(x,b),(x,c),(a,b),(a,c),(b,c),
(y,a),(y,b),(y,c),(x,y),共10种.
其中符合“质量在[80,85)和[95,100)内各有1个”的情况有
(x,a),(x,b),(x,c),(y,a),(y,b),(y,c),共6种.
设事件A 表示“抽出的5个草莓中,再任取2个,质量在[80,85)和[95,100)内各有1个”,
则P(A)==.
19.【答案】(1)x=80,y=50,p=0.40,q=0.25.(2).
【解析】(1)依题意,有
,解得,
所以p=0.40,q=0.25.
补全的频率分布直方图如图所示:
(2)根据题意,网购金额在(1,2]的群体中应抽取的人数为×5=3,
记这3人分别为A,B,C;
网购金额在(4,5]的群体中应抽取的人数为×5=2,
记这2人分别为D,E.
从这5人中随机选取2人,所含的基本事件为
{A,B},{A,C},{A,D},{A,E},{B,C},{B,D},
{B,E},{C,D},{C,E},{D,E},共 10种.
设事件M为“这2人来自不同群体”,则事件M所含的基本事件为
{A,D},{A,E},{B,D},{B,E},{C,D},{C,E},共6种,
所以事件M发生的概率为=.
20.【答案】B
【解析】甲、乙、丙、丁、戊站成一排,基本事件总数n=5×4×3×2×1=120,甲不在两端包含的基本事件个数m=3×4×3×2×1=72,∴甲不在两端的概率p=.故选B.
23.【答案】D
【解析】从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,基本事件总数n=5×5=25,抽得的第一张卡片上的数大于第二张卡片上的数包含的基本事件有:(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),共有m=10个基本事件,∴抽得的第一张卡片上的数大于第二张卡片上的数的概率P==.故选D.
24.【答案】C
【解析】从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,所有的基本事件为:(12),(13),(14),(15),(16),(17),(18),(19),(23),(24),(25),(26),(27),(28),(29),(34),(35),(36),(37),(38),(39),(45),(46),(47),(48),(49),(56),(57),(58),(59),(67),(68),(69),(78),(79),(89),共有36种不同的情况,且这些情况是等可能发生的,其中抽到在2张卡片上的数奇偶性不同的情况有20种,故抽到在2张卡片上的数奇偶性不同的概率P==,故选C.
25.【答案】
【解析】编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,
从中随机选取三个,3个数中含有1个2;2个2,没有2,3种情况,
所有的事件总数为:10,
这三个砝码的总质量为9克的事件只有:5,3,1或5,2,2两个,
所以:这三个砝码的总质量为9克的概率是:,
故答案为:.
26.【答案】0.3
【解析】设2名男生为a,b;3名女生为A,B,C,则任选2人的种数为ab,aA,aB,aC,bA,bB,Bc,AB,AC,BC共10种,其中全是女生为AB,AC,BC共3种,故选中的2人都是女同学的概率P==0.3,故答案为:0.3.
27.【答案】
【解析】给出四个函数:①y=–x,②y=–,③y=x3,④y=x,从四个函数中任选2个,基本事件有(①②),(①③),(①④),(②③),(②④),(③④),共n=6种,事件A:“所选2个函数的图象有且只有一个公共点”包含的基本事件有:①③,①④共2个,所以事件A:“所选2个函数的图象有且只有一个公共点”的概率为P(A)==.故答案为:.
28.【答案】(1)应从甲、乙、丙三个年级的学生志愿意者中分别抽取得3人,2人,2人;(2)①详见解析;②.
【解析】(1)由已知得甲、乙、丙三个年级的学生志愿者人数之比为3:2:2,
由于采用分层抽样的方法从中抽取7名同学,
∴应从甲、乙、丙三个年级的学生志愿意者中分别抽取得3人,2人,2人.
(2)①从抽取的7名同学中抽取2名同学的所有可能结果为:
{A,B},{A,C},{A,D},{A,E},{A,F},{A,G},{B,C},{B,D},
{B,E},{B,F},{B,G},{C,D},{C,E},{C,F},{C,G},{D,E},
{D,F},{D,G},{E,F},{E,G},{F,G},共21个.
②设抽取的7名学生中,来自甲年级的是A,B,C,
来自乙年级的是D,E,来自丙年级的是F,G,
M为事件“抽取的2名同学来自同一年级”,
则事件M包含的基本事件有:
{A,B},{A,C},{B,C},{D,E},{F,G},共5个基本事件,
∴事件M发生的概率P(M)=.
29.【答案】(1).(2).
【解析】(1)某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
从这6个国家中任选2个,所有基本事件有
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,B3),
(A2,A3),(A2,B1),(A2,B2),(A2,B3),
(A3,B1),(A3,B2),(A3,B3),
(B1,B2),(B1,B3),
(B2,B3),
共n=15种,
这2个国家都是亚洲国家包含的基本事件有(A1,A2),(A1,A3),(A2,A3),
共有m=3种,
∴这2个国家都是亚洲国家的概率P===.
(2)从亚洲国家和欧洲国家中各任选1个,包含的基本事件个数为9个,分别为:
(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),
(A2,B3),(A3,B1),(A3,B2),(A3,B3),
这2个国家包括A1但不包括B1包含的基本事件有:
(A1,B2),(A1,B3),共2个,
∴这2个国家包括A1但不包括B1的概率P=.
30.【答案】(1)0.6.(2)Y的所有可能值为900,300,–100;Y大于零的概率的估计值为0.8.
【解析】(1)这种酸奶一天的需求量不超过300瓶,当且仅当最高气温低于25,
由表格数据知,最高气温低于25的频率为=0.6,
所以这种酸奶一天的需求量不超过300瓶的概率的估计值为0.6.
3.2古典概型
知识
1.古典概型
(1)基本事件
在一次试验中,可能出现的每一个基本结果叫做基本事件.
基本事件有如下特点:
①任何两个基本事件是___________的.
②任何事件(除不可能事件)都可以表示成___________.
(2)古典概型
把具有特点:①试验中所有可能出现的基本事件只有___________个;②每个基本事件出现的可能性___________的概率模型称为古典概率模型,简称古典概型.
2.古典概型的概率公式
如果一次试验中,可能出现的结果有个,而且所有结果出现的可能性相等,那么每一个基本事件的概率都是;如果事件包含的基本事件有个,那么事件的概率为_______=_________.
3.(整数值)随机数的产生
(1)随机数与伪随机数
例如我们要产生1~25之间的随机整数,我们把25个大小形状相同的小球分别标上1,2,3,…,24,25,放入一个袋中,把它们充分搅拌,然后从中摸出一个,这个球上的数就称为随机数.
计算机或计算器产生的随机数是依照确定算法产生的数,具有周期性(周期很长),它们具有类似随机数的性质.因此,计算机或计算器产生的并不是真正的随机数,我们称它们为伪随机数.
(2)随机数的产生方法
课本中给出了两种产生随机数的方法:①利用带有PRB功能的计算器产生随机数;②用计算机软件产生随机数,比如用Excel软件产生随机数.
(3)用随机模拟方法估计概率
用计算机或计算器模拟试验的方法称为随机模拟方法或蒙特卡罗方法.
其基本步骤是:①建立概率模型;②进行模拟试验,可用计算器或计算机进行模拟试验;③统计试验的结果.
知识参考答案:
1.(1)①互斥 ②基本事件的和 (2)①有限 ②相等
2.
重点
重点
理解古典概型的概念及利用古典概型求解随机事件的概率
难点
判断一个试验是否是古典概型,分清在一个古典概型中某随机事件包含的基本事件的个数和试验中基本事件的总数
易错
利用古典概型的概率公式求解时,要注意试验的每个基本事件是等可能发生的
1.古典概型的判定
并不是所有的试验都是古典概型,只有同时满足有限性和等可能性这两个条件的试验才是古典概型.两个条件中只要有一个不满足就不是古典概型.
【例1】(1)在数轴上0~3之间任取一点x,观察x是否小于1.此试验是否为古典概型?为什么?
(2)从1,2,3,4四个数中任意取出两个数,观察所取两数之一是否是5.此试验是古典概型吗?试说明理由.
(3)投掷一颗质地非均匀的骰子,观察掷出的点数.此试验是否为古典概型?为什么?
【解析】(1)在数轴上0~3之间任取一点,此点可以在0~3之间的任一位置,且在每个位置上的可能性是相同的,具备等可能性.但试验结果有无限多个,不满足古典概型试验结果的有限性.因此不属于古典概型.
(2)此试验是古典概型,因为此试验的所有基本事件共有6个:(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),且每个事件的出现是等可能的,因此属于古典概型.
(3)投掷一颗质地非均匀的骰子,掷出的点数不是等可能出现的,质地较重的那一面朝下的可能性比较大,其对面的点数出现的可能性就比其他点数出现的可能性大,因此不属于古典概型.
2.古典概型的计算
求古典概型的概率的关键是正确列出基本事件,在写出基本事件后最好检验一下各基本事件发生的概率是否相同.求随机事件的概率的关键就是明晰它包含了几个基本事件.
要写出所有的基本事件可采用的方法较多,例如列举法、列表法、坐标系法、树形图法等.无论采用哪种方法,都要求按照一定的顺序进行,以做到不重不漏.
【例2】某中学调查了某班全部名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团
未参加书法社团
参加演讲社团
未参加演讲社团
(1)从该班随机选名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的名同学中,有5名男同学名女同学现从这名男同学和名女同学中各随机选人,求被选中且未被选中的概率.
【解析】(1)由调查数据可知,既未参加书法社团又未参加演讲社团的有人,
故至少参加上述一个社团的共有人,
所以从该班随机选名同学,该同学至少参加上述一个社团的概率为
(2)从这名男同学和名女同学中各随机选人,其一切可能的结果组成的基本事件有:
,共个.
根据题意,这些基本事件的出现是等可能的.
事件“被选中且未被选中”所包含的基本事件有:,共个.
因此被选中且未被选中的概率为.
【例3】某大学的教授从大二年级学生所选修的《消费者化学》的成绩中随机抽取40名学生的成绩,分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.
(1)求频率分布直方图中实数a的值;
(2)若该校大二年级共有640名学生,试估计该校大二年级所选修的《消费者化学》的成绩不低于60分的学生人数;
(3)若从样本中成绩在[40,50)与[90,100]内的所有学生中随机选取2名学生,求这2名学生的成绩之差的绝对值不大于10的概率.
(3)成绩在[40,50)内的学生人数为40×0.05=2,分别记为A,B;
成绩在[90,100]内的学生人数为40×0.1=4,分别记为C,D,E,F.
若从成绩在[40,50)与[90,100]内的所有学生中随机选取2名学生,
则所有的基本事件有(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15个.
若这2名学生的成绩都在[40,50)内或都在[90,100]内,则这2名学生的成绩之差的绝对值一定不大于10;若1名学生的成绩在[40,50)内,另1名学生的成绩在[90,100]内,则这2名学生的成绩之差的绝对值一定大于10.
记“这2名学生的成绩之差的绝对值不大于10”为事件M,
则事件M包含的基本事件有(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共7个.
所以所求的概率为P(M)=.
【名师点睛】概率问题常与统计问题综合考查,在此类问题中,注意灵活运用概率与统计的知识求解.
3.用随机模拟估计概率
用随机模拟估计概率的关键是用相应的整数表示试验的结果,然后按实际需要将所得的随机数分为若干个一组(比如试验要求随机抽取三个球就三个数据一组),明晰所求事件的特点后去找符合要求的数据组,即可求解概率.
【例4】已知某运动员每次投篮命中的概率都为40%,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中;5,6,7,8,9,0表示不命中,再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:
137 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为
A.0.40 B.0.30
C.0.35 D.0.25
【答案】B
【解析】由题意,得在20组模拟数据中,表示该运动员三次投篮恰有两次命中的数据有:137、191、271、932、812、393,共6个数据,故该运动员三次投篮恰有两次命中的概率为.故选B.
4.混淆“等可能”与“非等可能”
【例5】从5名男生和3名女生中任选1人去参加演讲比赛,求选中女生的概率.
【错解】从8人中选出1人的结果有“男生”“女生”两种,则选中女生的概率为.
【错因分析】因为男生人数多于女生人数,所以选中男生的机会大于选中女生的机会,它们不是等可能的.
【正解】选出1人的所有可能的结果有8种,即共有8个基本事件,其中选中女生的基本事件有3个,故选中女生的概率为.
【名师点睛】利用古典概型的概率公式求解时,注意需满足两个条件:
(1)所有的基本事件只有有限个;
(2)试验的每个基本事件是等可能发生的.
基础训练
1.下列有关古典概型的四种说法:
①试验中所有可能出现的基本事件只有有限个;
②每个事件出现的可能性相等;
③每个基本事件出现的可能性相等;
④已知基本事件总数为n,若随机事件A包含k个基本事件,则事件A发生的概率P(A)=.
其中所有正确说法的序号是
A.①②④ B.①③ C.③④ D.①③④
2.盒中有2个红色的变形金刚,2个白色的变形金刚,2个黑色的变形金刚,从里面任意取2个变形金刚,不是基本事件的为
A.{恰好2个红色的变形金刚} B.{恰好2个黑色的变形金刚}
C.{恰好2个白色的变形金刚} D.{至少1个红色的变形金刚}
3.下列试验是古典概型的是
A.在适宜的条件下,种下一粒种子,观察它是否发芽
B.口袋里有2个白球和2个黑球,这4个球除颜色外完全相同,从中任取一球
C.向一个圆面内随机投一点
D.射击运动员向一靶心进行射击,试验结果为命中10环,命中9环,……,命中0环
4.把一枚骰子投掷两次,观察出现的点数,记第一次出现的点数为a,第二次出现的点数为b,则方程组只有一组解的概率为
A. B. C. D.
5.从甲、乙等5名学生中随机选出2名,则甲被选中的概率为
A. B. C. D.
6.甲、乙两人一起去游览公园,他们约定各自独立地从1号到6号景点中任选4个进行游览,每个景点参观1小时,则最后一小时他们在同一个景点的概率是
A. B. C. D.
7.在平面直角坐标系中,从下列5个点:A(0,0),B(2,0),C(1,1),D(0,2),E(2,2)中任取3个,这三点能构成三角形的概率是
A. B. C. D.1
能力提升
8.某天放学以后,教室里还剩下2位男同学和2位女同学.若他们依次走出教室,则第2位走出的是男同学的概率是
A. B. C. D.
9.某大学餐饮中心为了解新生的饮食习惯,在全校大一学生中进行了抽样调查.已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,则至多有1人喜欢甜品的概率为
A.0.3 B.0.4 C.0.6 D.0.7
10.某城市有连接8个小区A,B,C,D,E,F,G,H和市中心O的整齐方格形道路网,每个小方格均为正方形,如图所示.某人从道路网中随机地选择一条最短路径,由小区A前往小区H,则他经过市中心O的概率为
A. B. C. D.
11.现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率.先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 0293 7140 9857 0347
4373 8636 6947 1417 4698
0371 6233 2616 8045 6011
3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为
A.0.852 B.0.819 2 C.0.8 D.0.75
12.从正六边形的6个顶点中随机选出4个,以它们作为顶点的四边形是矩形的概率为____________.
13.一个口袋内装有1个白球和编号分别为1,2,3的3个黑球,它们的大小、质地相同,从中任意摸出2个球.
(1)共有多少个基本事件?每个基本事件是否等可能出现?该试验是古典概型吗?
(2)“摸出的2个球都是黑球”记为事件A,则事件A包含哪几个基本事件?
14.甲、乙两名运动员为了争夺某比赛最后一个参赛名额,共进行了7轮比赛,得分情况如茎叶图所示.
(1)根据茎叶图分析甲、乙两名运动员中谁的比赛成绩更稳定?
(2)若从甲运动员的7轮比赛中任选3个不低于80且不高于90的得分,求这3个得分与其7轮比赛的平均得分的差的绝对值都不超过2的概率.
15.小陈以游戏方式决定是参加学校合唱团还是参加学校足球队.游戏规则:从A1,A2,A3,A4,A5,A6(如图)这6个点中任取2个点,记选取的在y轴上的点的个数为X.若X=0就参加学校合唱团,否则就参加学校足球队.
(1) 请列出从A1,A2,A3,A4,A5,A6中任取2个点的所有可能情况;
(2)求小陈不参加学校合唱团的概率.
16.一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外,其他完全相同.现随机有放回地抽取3次,每次抽取一张,将抽取的卡片上的数字依次记为a,b,C.
(1)求“抽取的卡片上的数字满足a+b=c”的概率;
(2)求“抽取的卡片上的数字a,b,c不完全相同”的概率.
17.从含有两件正品a1,a2和一件次品b1的三件产品中每次任取一件,连续取两次.
(1)若每次取出后不放回,求取出的两件产品中恰有一件次品的概率;
(2)若每次取出后放回,求取出的两件产品中恰有一件次品的概率.
18.从一批草莓中随机抽取n个,其质量(单位:g)的频数分布表如下:
分组
[80,85)
[85,90)
[90,95)
[95,100)
频数
10
50
x
15
已知从这n个草莓中随机抽取1个,其质量在[90,95)内的概率为.
(1)求n,x的值;
(2)用分层抽样的方法从质量在[80,85)和[95,100)内的草莓中抽取5个,再从这5个草莓中任取2个,求质量在[80,85)和[95,100)内各有1个的概率.
19.福建某网络营销部门随机抽查了福州市200名网友在2017年“双十一”的网购金额,所得数据如下:
网购金额/千元
人数
频率
(0,1]
16
0.08
(1,2]
24
0.12
(2,3]
x
p
(3,4]
y
q
(4,5]
16
0.08
(5,6]
14
0.07
合计
200
1.00
已知网购金额不超过3千元与超过3千元的人数之比恰为3∶2.
(1)试确定x,y,p,q的值,并补全频率分布直方图;
(2)该营销部门为了了解该市网友的购物体验,从这200名网友中,用分层抽样的方法从网购金额在(1,2]和(4,5]的两个群体中抽取5人进行问卷调查,若需从这5人中随机选取2人继续访谈,求这2人来自不同群体的概率.
真题练习
20.(2018?全国)甲、乙、丙、丁、戊站成一排,甲不在两端的概率
A. B. C. D.
21.(2018?新课标Ⅱ)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是
A. B. C. D.
22.(2019?天津模拟)有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为
A. B. C. D.
23.(2017?新课标Ⅱ)从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
A. B. C. D.
24.(2019?山东模拟)从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,每次抽取1张,则抽到在2张卡片上的数奇偶性不同的概率是
A. B. C. D.
25.(2018?上海)有编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,从中随机选取三个,则这三个砝码的总质量为9克的概率是____________(结果用最简分数表示).
26.(2019?江苏模拟)某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率为____________.
27.(2017?上海)已知四个函数:①y=–x,②y=–,③y=x3,④y=x,从中任选2个,则事件“所选2个函数的图象有且仅有一个公共点”的概率为__________.
28.(2019?天津模拟)己知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.
29.(2019?山东文科模拟)某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括A1但不包括B1的概率.
30.(2017?全国卷Ⅲ文)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:°C)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温
[10,15)
[15,20)
[20,25)
[25,30)
[30,35)
[35,40)
天数
2
16
36
25
7
4
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
参考答案
1
2
3
4
5
6
7
8
9
10
11
20
21
22
23
24
D
D
B
B
B
D
C
A
D
B
D
B
C
C
D
C
1.【答案】D
【解析】②中所说的事件不一定是基本事件,所以②不正确;根据古典概型的特点及计算公式可知①③④正确.故选D.
2.【答案】D
【解析】至少1个红色的变形金刚包含1红1白或1红1黑或2红,所以{至少1个红色的变形金刚}不是基本事件,其他项中的事件都是基本事件.故选D.
5.【答案】B
【解析】设这5名学生分别是甲、乙、丙、丁、戊,从中随机选出2名的方法有(甲,乙),(甲,丙),(甲,丁),(甲,戊),(乙,丙),(乙,丁),(乙,戊),(丙,丁),(丙,戊),(丁,戊),共有10种,其中甲被选中有4种,所以所求概率为=.
6.【答案】D
【解析】甲、乙最后一小时所在的景点共有36种情况,甲、乙最后一小时在同一个景点共有6种情况.由古典概型的概率公式,知后一小时他们在同一个景点的概率是=.
7.【答案】C
【解析】从5个点中任取3个点,有ABC,ABD,ABE,ACD,ACE,ADE,BCD,BCE,BDE,CDE,共10个基本事件,其中ACE,BCD 2个事件中的点不能构成三角形,故能构成三角形的概率为=.
8.【答案】A
【解析】2位男同学和2位女同学走出教室的所有可能顺序有(女,女,男,男),(女,男,女,男),(女,男,男,女),(男,男,女,女),(男,女,男,女),(男,女,女,男),共6种,所以第2位走出的是男同学的概率是P==,故选A.
9.【答案】D
【解析】记2名喜欢甜品的学生分别为a1,a2,3名不喜欢甜品的学生分别为b1,b2,b3.从5名数学系学生中任取3人的所有可能结果组成的基本事件有10个,分别为{a1,a2,b1},{a1,a2,b2},{a1,a2,b3},{a1,b1,b2},{a1,b1,b3},{a1,b2,b3},{a2,b1,b2},{a2,b1,b3},{a2,b2,b3},{b1,b2,b3}.记事件A表示“至多有1人喜欢甜品”,则事件A所包含的基本事件分别为{a1,b1,b2},{a1,b1,b3},{a1,b2,b3},{a2,b1,b2},{a2,b1,b3},{a2,b2,b3},{b1,b2,b3},共7个.根据古典概型的概率计算公式,得至多有1人喜欢甜品的概率P(A)==0.7,故选D.
10.【答案】B
【解析】由题意,知此人从小区A前往小区H的所有最短路径为A→B→C→E→H,A→B→O→E→H,A→B→O→G→H,A→D→O→E→H,A→D→O→G→H,A→D→F→G→H,共6条.记“此人经过市中心O”为事件M,则M包含的基本事件为A→B→O→E→H,A→B→O→G→H,A→D→O→E→H,A→D→O→G→H,共4条,所以P(M)==,即他经过市中心O的概率为.
13.【答案】(1)每个基本事件是等可能出现的,这个试验是古典概型;(2)详见解析.
【解析】(1)任意摸出2个球,共有
(白,黑1),(白,黑2),(白,黑3),(黑1,黑2),(黑1,黑3),(黑2,黑3),
共6个基本事件,且每个基本事件是等可能出现的,这个试验是古典概型.
(2)事件A包含(黑1,黑2),(黑1,黑3),(黑2,黑3),共3个基本事件.
14.【答案】(1)乙运动员的比赛成绩更稳定;(2).
【解析】(1)由茎叶图,可知甲、乙两名运动员7轮比赛的得分情况为
甲:78,81,84,85,84,85,91;乙:79,84,84,86,87,84,91.
所以甲运动员的平均得分=84,方差=,
乙运动员的平均得分=85,方差=,
由于>,故乙运动员的比赛成绩更稳定.
(2)由(1)知,甲运动员的7轮比赛得分中不低于80且不高于90的得分共有5个,
分别是81,84,85,84,85.
从中任选的3个得分记为(x,y,z),则不同的结果有
(81,84,85),(81,84,84),(81,84,85),(81,85,84),(81,85,85),
(81,84,85),(84,85,84),(84,85,85),(84,84,85),(85,84,85),共10种,
这3个得分与其7轮比赛的平均得分的差的绝对值都不超过2的情况有
(84,85,84),(84,85,85),(84,84,85),(85,84,85),共4种.
所以所求的概率P==.
15.【答案】(1)详见解析;(2).
【解析】(1)从A1,A2,A3,A4,A5,A6中任取2个点包含的所有情况为
{A1,A2},{A1,A3},{A1,A4},{A1,A5},{A1,A6},
{A2,A3},{A2,A4},{A2,A5},{A2,A6},
{A3,A4},{A3,A5},{A3,A6},{A4,A5},{A4,A6},{A5,A6},共有15种.
(2)当X=0时,所取的2个点均不在y轴上,即从A1,A2,A5,A6中任取2个点,
所有可能的情况为{A1,A2},{A1,A5},{A1,A6},{A2,A5},{A2,A6},{A5,A6},共6种,
所以小陈参加学校合唱团的概率为=,
所以小陈不参加学校合唱团的概率P=1–=.
16.【答案】(1).(2).
【解析】(1)由题意,(a,b,c)所有可能的结果为
(1,1,1),(1,1,2),(1,1,3),(1,2,1),(1,2,2),(1,2,3),
(1,3,1),(1,3,2),(1,3,3),(2,1,1),(2,1,2),(2,1,3),
(2,2,1),(2,2,2),(2,2,3),(2,3,1),(2,3,2),(2,3,3),
(3,1,1),(3,1,2),(3,1,3),(3,2,1),(3,2,2),(3,2,3),
(3,3,1),(3,3,2),(3,3,3),共27种.
设“抽取的卡片上的数字满足a+b=c”为事件A,则事件A包括
(1,1,2),(1,2,3),(2,1,3),共3种,所以P(A)==.
因此,“抽取的卡片上的数字满足a+b=c”的概率为.
(2)设“抽取的卡片上的数字a,b,c不完全相同”为事件B,则事件包括
(1,1,1),(2,2,2),(3,3,3),共3种,
所以P(B)=1–P()=1–=,
因此,“抽取的卡片上的数字a,b,c不完全相同”的概率为.
17.【答案】(1).(2).
【解析】(1)不放回地连续取两次,其基本事件为
(a1,a2),(a1,b1),(a2,a1),(a2,b1),(b1,a1),(b1,a2),共 6个.
记“取出的两件产品中恰有一件次品”为事件A,
则事件A由(a1,b1),(a2,b1),(b1,a1),(b1,a2)这4个基本事件组成,
因而P(A)==.
(2)有放回地连续取两次,其基本事件为
(a1,a1),(a1,a2),(a1,b1),(a2,a1),(a2,a2),(a2,b1),
(b1,a1),(b1,a2),(b1,b1),共9个.
记“取出的两件产品中恰有一件次品”为事件B,
则事件B由(a1,b1),(a2,b1),(b1,a1),(b1,a2)这4个基本事件组成,
因而P(B)=.
18.【答案】(1)x=20,n=95.(2).
【解析】(1)依题意可得,解得x=20,n=95.
(2)若采用分层抽样的方法从质量在[80,85)和[95,100)内的草莓中抽取5个,
则质量在[80,85)内的个数为×5=2,记为x,y,
在[95,100)内的个数为×5=3,记为a,b,c.
从抽出的5个草莓中,任取2个,有
(x,a),(x,b),(x,c),(a,b),(a,c),(b,c),
(y,a),(y,b),(y,c),(x,y),共10种.
其中符合“质量在[80,85)和[95,100)内各有1个”的情况有
(x,a),(x,b),(x,c),(y,a),(y,b),(y,c),共6种.
设事件A 表示“抽出的5个草莓中,再任取2个,质量在[80,85)和[95,100)内各有1个”,
则P(A)==.
19.【答案】(1)x=80,y=50,p=0.40,q=0.25.(2).
【解析】(1)依题意,有
,解得,
所以p=0.40,q=0.25.
补全的频率分布直方图如图所示:
(2)根据题意,网购金额在(1,2]的群体中应抽取的人数为×5=3,
记这3人分别为A,B,C;
网购金额在(4,5]的群体中应抽取的人数为×5=2,
记这2人分别为D,E.
从这5人中随机选取2人,所含的基本事件为
{A,B},{A,C},{A,D},{A,E},{B,C},{B,D},
{B,E},{C,D},{C,E},{D,E},共 10种.
设事件M为“这2人来自不同群体”,则事件M所含的基本事件为
{A,D},{A,E},{B,D},{B,E},{C,D},{C,E},共6种,
所以事件M发生的概率为=.
20.【答案】B
【解析】甲、乙、丙、丁、戊站成一排,基本事件总数n=5×4×3×2×1=120,甲不在两端包含的基本事件个数m=3×4×3×2×1=72,∴甲不在两端的概率p=.故选B.
23.【答案】D
【解析】从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,基本事件总数n=5×5=25,抽得的第一张卡片上的数大于第二张卡片上的数包含的基本事件有:(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),共有m=10个基本事件,∴抽得的第一张卡片上的数大于第二张卡片上的数的概率P==.故选D.
24.【答案】C
【解析】从分别标有1,2,…,9的9张卡片中不放回地随机抽取2次,所有的基本事件为:(12),(13),(14),(15),(16),(17),(18),(19),(23),(24),(25),(26),(27),(28),(29),(34),(35),(36),(37),(38),(39),(45),(46),(47),(48),(49),(56),(57),(58),(59),(67),(68),(69),(78),(79),(89),共有36种不同的情况,且这些情况是等可能发生的,其中抽到在2张卡片上的数奇偶性不同的情况有20种,故抽到在2张卡片上的数奇偶性不同的概率P==,故选C.
25.【答案】
【解析】编号互不相同的五个砝码,其中5克、3克、1克砝码各一个,2克砝码两个,
从中随机选取三个,3个数中含有1个2;2个2,没有2,3种情况,
所有的事件总数为:10,
这三个砝码的总质量为9克的事件只有:5,3,1或5,2,2两个,
所以:这三个砝码的总质量为9克的概率是:,
故答案为:.
26.【答案】0.3
【解析】设2名男生为a,b;3名女生为A,B,C,则任选2人的种数为ab,aA,aB,aC,bA,bB,Bc,AB,AC,BC共10种,其中全是女生为AB,AC,BC共3种,故选中的2人都是女同学的概率P==0.3,故答案为:0.3.
27.【答案】
【解析】给出四个函数:①y=–x,②y=–,③y=x3,④y=x,从四个函数中任选2个,基本事件有(①②),(①③),(①④),(②③),(②④),(③④),共n=6种,事件A:“所选2个函数的图象有且只有一个公共点”包含的基本事件有:①③,①④共2个,所以事件A:“所选2个函数的图象有且只有一个公共点”的概率为P(A)==.故答案为:.
28.【答案】(1)应从甲、乙、丙三个年级的学生志愿意者中分别抽取得3人,2人,2人;(2)①详见解析;②.
【解析】(1)由已知得甲、乙、丙三个年级的学生志愿者人数之比为3:2:2,
由于采用分层抽样的方法从中抽取7名同学,
∴应从甲、乙、丙三个年级的学生志愿意者中分别抽取得3人,2人,2人.
(2)①从抽取的7名同学中抽取2名同学的所有可能结果为:
{A,B},{A,C},{A,D},{A,E},{A,F},{A,G},{B,C},{B,D},
{B,E},{B,F},{B,G},{C,D},{C,E},{C,F},{C,G},{D,E},
{D,F},{D,G},{E,F},{E,G},{F,G},共21个.
②设抽取的7名学生中,来自甲年级的是A,B,C,
来自乙年级的是D,E,来自丙年级的是F,G,
M为事件“抽取的2名同学来自同一年级”,
则事件M包含的基本事件有:
{A,B},{A,C},{B,C},{D,E},{F,G},共5个基本事件,
∴事件M发生的概率P(M)=.
29.【答案】(1).(2).
【解析】(1)某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
从这6个国家中任选2个,所有基本事件有
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,B3),
(A2,A3),(A2,B1),(A2,B2),(A2,B3),
(A3,B1),(A3,B2),(A3,B3),
(B1,B2),(B1,B3),
(B2,B3),
共n=15种,
这2个国家都是亚洲国家包含的基本事件有(A1,A2),(A1,A3),(A2,A3),
共有m=3种,
∴这2个国家都是亚洲国家的概率P===.
(2)从亚洲国家和欧洲国家中各任选1个,包含的基本事件个数为9个,分别为:
(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),
(A2,B3),(A3,B1),(A3,B2),(A3,B3),
这2个国家包括A1但不包括B1包含的基本事件有:
(A1,B2),(A1,B3),共2个,
∴这2个国家包括A1但不包括B1的概率P=.
30.【答案】(1)0.6.(2)Y的所有可能值为900,300,–100;Y大于零的概率的估计值为0.8.
【解析】(1)这种酸奶一天的需求量不超过300瓶,当且仅当最高气温低于25,
由表格数据知,最高气温低于25的频率为=0.6,
所以这种酸奶一天的需求量不超过300瓶的概率的估计值为0.6.
