4.2.2 圆与圆的位置关系 学案
文档属性
| 名称 | 4.2.2 圆与圆的位置关系 学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-25 11:17:04 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
4.2.2圆与圆的位置关系
一、圆与圆的位置关系
1.圆与圆的位置关系
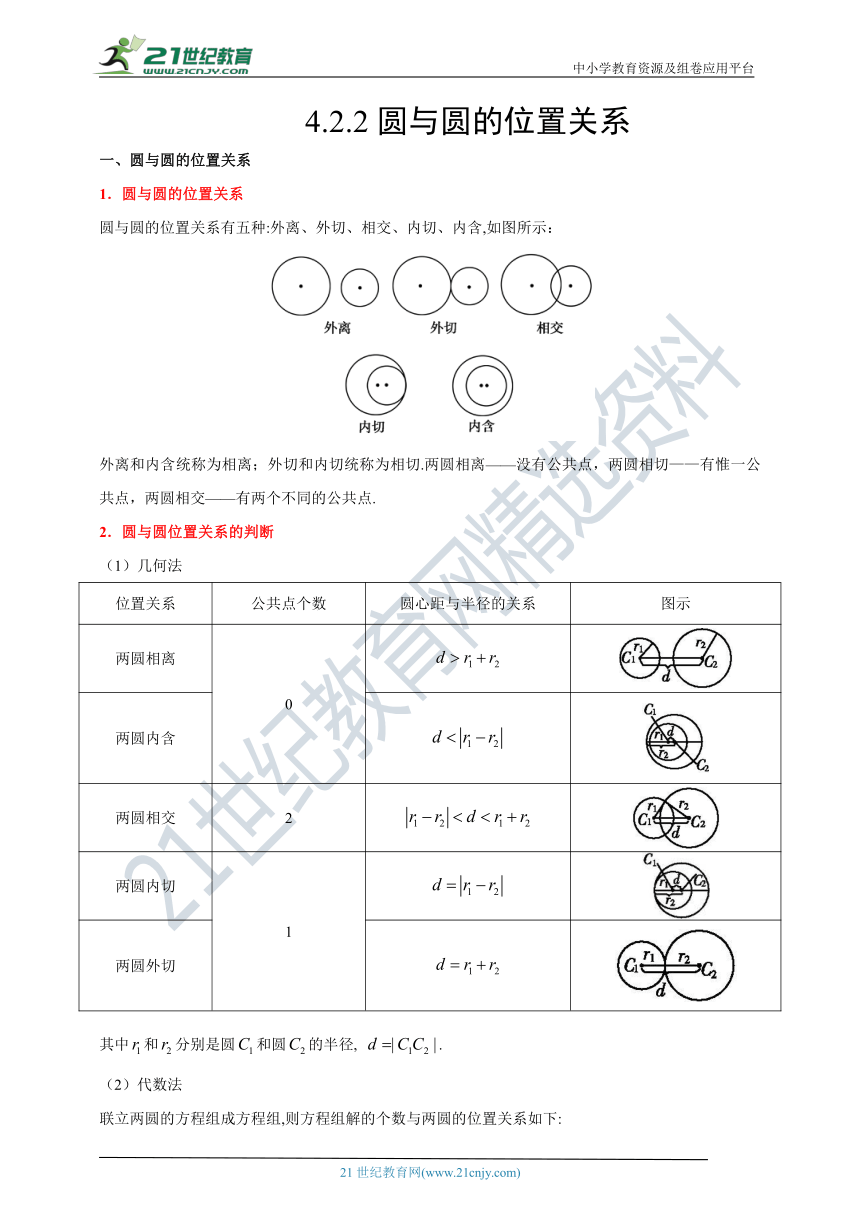
圆与圆的位置关系有五种:外离、外切、相交、内切、内含,如图所示:
外离和内含统称为相离;外切和内切统称为相切.两圆相离——没有公共点,两圆相切——有惟一公共点,两圆相交——有两个不同的公共点.
2.圆与圆位置关系的判断
(1)几何法
位置关系 公共点个数 圆心距与半径的关系 图示
两圆相离 0
两圆内含
两圆相交 2
两圆内切 1
两圆外切
其中和分别是圆和圆的半径, .
(2)代数法
联立两圆的方程组成方程组,则方程组解的个数与两圆的位置关系如下:
方程组解的个数 2 1 0
两圆的公共点个数 2 1 0
两圆的位置关系 . 相离或内含
知识参考答案:
一、2.(2)相交 外切或内切
【例1】求与圆外切,且与直线相切于点M(3,)的圆的方程.
【解析】设所求圆的方程为,由于该圆与圆外切,则圆心距等于半径之和,故有 ①.
又与直线相切于点M(3,),则可知圆心与切点的连线与直线垂直,有 ②,
?③,解①②③得.
故所求圆的方程为.
【例2】已知两圆和.
(1)试判断两圆的位置关系;
(2)求公共弦所在直线的方程;
(3)求公共弦的长度.
【解析】(1)将两圆方程配方化为标准方程,
则圆的圆心为,半径;圆C2的圆心为,半径.
又,,.
∴,∴两圆相交.
(2)将两圆方程相减,得公共弦所在直线的方程为.
(3)方法一:两方程联立,得方程组,
两式相减得③,把③代入②得,
∴.
∴,或.
∴交点坐标为和.
∴两圆的公共弦长为.
【例3】已知圆C1:x2+y2-10x-10y=0和圆C2:x2+y2-6x+2y-40=0相交,圆C过原点O,半径长为,圆心C在已知两圆公共弦所在的直线上,求圆C的方程.
【解析】设圆C1与圆C2交于A,B两点,两圆的方程相减,消去二次项得到一个二元一次方程x+3y-10=0,此方程为公共弦AB所在直线的方程.
又已知圆C的圆心C在两圆公共弦所在的直线上,即在直线AB上,设C(a,b),则a+3b-10=0 ①,由|CO|=,得a2+b2=10 ②,①②联立,解得a=1,b=3,
所以圆C的方程为(x-1)2+(y-3)2=10.
【例4】已知圆,圆,动圆与圆外切并且与圆内切,圆心的轨迹为曲线.求的方程.
【解析】由已知得圆的圆心为,半径长,圆的圆心为,半径长.
设动圆的圆心为,半径长为.
∵圆与圆外切并且与圆内切,∴.
由两点间距离公式得,即,两边平方化简得的方程为.
【例5】求半径长为4,与圆相切,且和直线相切的圆的方程.
【正解】设所求圆的方程为,圆心为.又圆与直线相切且半径长为4,故圆心为或.圆的圆心为,半径长.若两圆相切,则或.作分类讨论:
当取时,或(无解),故,此时所求圆的方程为或.
当取时,或(无解),∴,此时所求圆的方程为或.
综上所述,所求圆的方程为或或或.
【例6】已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴、y轴上的截距相等,求切线的方程;
(2)从圆C外一点P(x1,y1)向圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使|PM|最小的点P的坐标.
解:(1)由方程x2+y2+2x-4y+3=0知,
圆心为(-1,2),半径为.
当切线过原点时,设切线方程为y=kx,
则=.
所以k=2±,即切线方程为y=(2±)x.
当切线不过原点时,设切线方程为x+y=a,
则=.所以a=-1或a=3,
即切线方程为x+y+1=0或x+y-3=0.
所以切线方程为y=(2+)x或y=(2-)x或x+y+1=0或x+y-3=0.
(2)设P(x1,y1).因为|PO|2+r2=|PC|2,
所以x21+y21+2=(x1+1)2+(y1-2)2,
即2x1-4y1+3=0.
要使|PM|最小,只要|PO|最小即可.
当直线PO垂直于直线2x-4y+3=0时,
即直线PO的方程为2x+y=0时,|PM|最小,
此时P点即为两直线的交点,得P点坐标(-,).
课时同步训练
1.圆与圆的位置关系为
A.内切 B.相交
C.外切 D.相离
2.圆O1:x2+y2=16和圆O2:x2+y2-4x+8y+4=0关于直线l对称,则l的方程为( )
A.x+2y-5=0
B.x-2y-5=0
C.x+2y+5=0
D.x-2y+5=0
3.圆x2+y2-4x+6y=0和圆x2+y2-6x=0交于A,B两点,则直线AB的方程是( )
A.x+y+3=0 B.3x-y-9=0
C.x+3y=0 D.4x-3y+7=0
4.已知是圆上的点,是圆上的点,则的最小值为
A.4 B.
C. D.2
5.若圆O:x2+y2=4与圆C:x2+y2+4x-4y+4=0关于直线l对称,则直线l的方程是
A.x+y=0 B.x-y=0
C.x+y+2=0 D.x-y+2=0
6.3.两圆x2+y2-4x+2y+1=0与x2+y2+4x-4y-1=0的公切线有( )
A.1条 B.2条
C.3条 D.4条
8.若半径为1的圆与圆x2+y2=4相切,则动圆圆心的轨迹方程是__________.
9.已知圆C1:x2+y2-2mx+4y+m2-5=0,圆C2:x2+y2+2x=0.
(1)m=1时,圆C1与圆C2有什么位置关系?
(2)是否存在m使得圆C1与圆C2内含?
10.已知动圆C与圆C1:(x-3)2+y2=4,圆C2:(x+3)2+y2=4中的一个外切、一个内切,求动圆圆心C的轨迹方程.
11.若圆始终平分圆的周长,则,应满足的关系式是
A. B.
C. D.
12.若集合,,且,则a的取值范围是
A.a≤1 B.a≥5
C.1≤a≤5 D.a≤5
13.已知半径为1的动圆与圆(x-5)2+(y+7)2=16相切,则动圆圆心的轨迹方程是
A.(x-5)2+(y+7)2=25
B.(x-5)2+(y+7)2=17或(x-5)2+(y+7)2=15
C.(x-5)2+(y+7)2=9
D.(x-5)2+(y+7)2=25或(x-5)2+(y+7)2=9
14.两圆相交于两点和,两圆圆心都在直线上,则的值为 .
15.已知圆M:截直线所得线段的长度是,则圆M与圆N:的位置关系是
A.内切 B.相交
C.外切 D.相离
1.【答案】B
【解析】两圆的圆心距为,半径分别为,且,所以两圆相交.故选B.
2答案:B
解析:两圆关于直线l对称,则直线l是两圆圆心O1(0,0),O2(2,-4)的垂直平分线.
3.答案:C
解析:两圆方程相减,得公共弦所在直线的方程为x+3y=0.
4.【答案】D
【解析】∵,∴圆内含于圆,则|MN|的最小值为.
5.【答案】D
【解析】圆C的标准方程为(x+2)2+(y-2)2=4,故圆心C的坐标为(-2,2).
因为圆O与圆C关于直线l对称,所以直线l过OC的中点(-1,1),且垂直于OC,
又kOC=-1,故直线l的斜率为1,直线l的方程为y-1=x-(-1),即x-y+2=0.故选D.
6.答案:C
解析:判断两圆的位置关系,即可知它们公切线的条数.外离、外切、相交、内切、内含的公切线的条数,分别有4条、3条、2条、1条、0条.这两圆外切,故选C.
7.【答案】1
∴x2+y2=9或x2+y2=1.
9.【解析】(1)∵m=1,∴两圆的方程分别可化为C1:(x-1)2+(y+2)2=9,C2:(x+1)2+y2=1.
两圆的圆心距d==2.
又r1+r2=3+1=4,r1-r2=3-1=2,
∴r1-r2
圆C1可化为(x-m)2+(y+2)2=9,圆心C1(m,-2),
则d=<3-1,
即(m+1)2<0,显然不等式无解.
故不存在m使得圆C1与圆C2内含.
10.解:设动圆圆心C的坐标为(x,y),半径为r.
由已知,得圆C1的圆心C1(3,0),半径r1=2;
圆C2的圆心C2(-3,0),半径r2=2.
依题意,得或.
∴|CC1|-|CC2|=4或|CC1|-|CC2|=-4.
即-=±4,
整理得5x2-4y2-20=0,
即为所求动圆圆心C的轨迹方程.
11.【答案】B
【解析】由题意得两圆的公共弦经过圆的圆心,两圆的公共弦所在直线方程为,则.
12.【答案】D
【解析】等价于B?A.当a>1时,集合A和B分别代表圆x2+y2=16和圆x2+(y-2)2 =a-1上及内部的点,容易得出当B对应的圆的半径小于或等于2时符合题意,则0
【解析】由已知,圆(x-5)2+(y+7)2=16的圆心为(5,-7),半径为4,由半径为1的动圆与圆(x-5)2+(y+7)2=16相切,可能外切或内切,设动圆圆心为G(x,y).
当两圆内切时,有圆心距为半径之差,即(x-5)2+(y+7)2=9.
当两圆外切时,圆心距为半径之和,有(x-5)2+(y+7)2=25. 故选D.
14.【答案】3
【解析】由题意知,线段的中点在直线上,且,解得,又,所以,所以.
15.【答案】B
【解析】由()得(),所以圆的圆心为,半径为,因为圆截直线所得线段的长度是,所以,解得,圆的圆心为,半径为,所以,,,因为,所以圆与圆相交,故选B.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
