2019-2020学年高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.2.2椭圆的简单几何性质(29张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.2.2椭圆的简单几何性质(29张) |

|
|
| 格式 | zip | ||
| 文件大小 | 855.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-26 00:00:00 | ||
图片预览








文档简介
课件29张PPT。2.2.2 椭圆的简单几何性质1.掌握椭圆的范围、对称性、离心率等简单几何性质.
2.会根据椭圆的标准方程画出它的几何图形,并能根据几何性质解决一些简单问题.
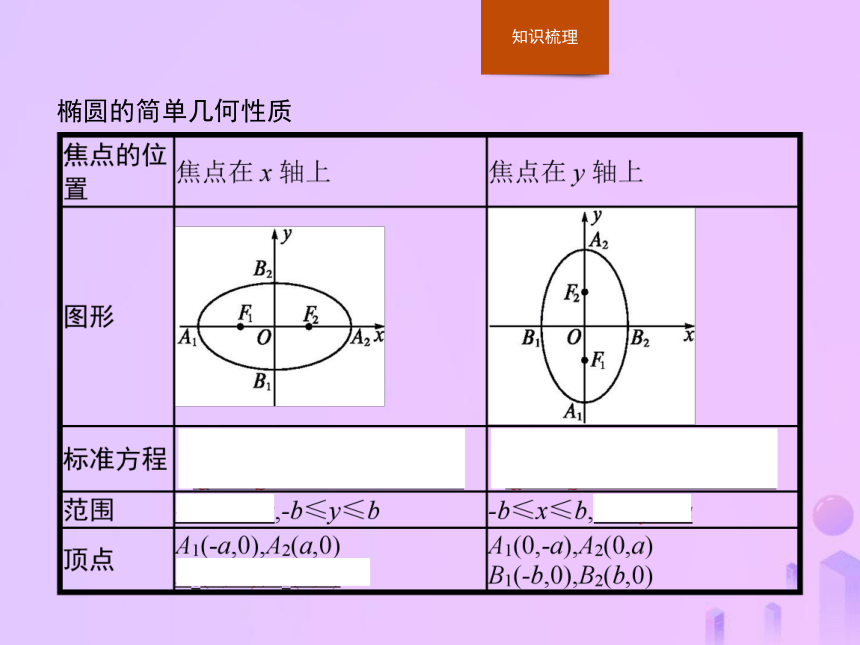
3.理解直线与椭圆的位置关系.椭圆的简单几何性质 【做一做1】 椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的2倍,则m的值为( )答案:C 【做一做2】 椭圆x2+4y2=1的离心率为( )答案:A 【做一做3】 椭圆16x2+9y2=144的焦点坐标是 ,顶点坐标是 .?2.直线与椭圆的位置关系
剖析:(1)直线与椭圆有三种位置关系:
①相交——直线与椭圆有两个不同的公共点;
②相切——直线与椭圆有且只有一个公共点;
③相离——直线与椭圆没有公共点.
(2)直线与椭圆的位置关系的判断:
我们把直线与椭圆的位置关系问题转化为直线与椭圆的公共点问题,而直线与椭圆的公共点问题,又可以转化为它们的方程所组成的方程组的解的问题,而它们的方程所组成的方程组的解的问题又可以转化为一元二次方程解的问题,一元二次方程解的问题可以通过判别式来判断,因此,直线和椭圆的位置关系,可由相应的一元二次方程的判别式来判断.判断方法:将直线方程和椭圆的方程联立,消去一个未知数,得到一个一元二次方程,若Δ>0,则直线与椭圆相交;若Δ=0,则直线与椭圆相切;若Δ<0,则直线与椭圆相离.知识拓展由弦长公式可知,求弦长时可以不求出交点坐标,只需先将方程联立,整理成关于x(或y)的一元二次方程,再根据一元二次方程根与系数的关系求出x1+x2,x1x2(或y1+y2,y1y2),代入弦长公式即可.题型一题型二题型三题型四由方程求椭圆的几何性质题型五分析:先根据点在椭圆上,求出方程中实数m的值,再将方程化为标准形式,确定焦点位置及a,b,c的值,最后写出几何性质.题型一题型二题型三题型四题型五反思已知椭圆的方程讨论其几何性质时,应先把椭圆的方程化成标准形式,找准a与b,再正确地写出其相关性质.在求顶点坐标和焦点坐标时,应注意焦点所在的坐标轴.题型一题型二题型三题型四【变式训练1】 椭圆6x2+y2=6的长轴端点坐标为 ( )答案:D 题型五题型一题型二题型三题型四利用椭圆的几何性质求标准方程
【例2】 求适合下列条件的椭圆的标准方程:
(1)长轴长是6,
(2)焦点在x轴上,且一个焦点与短轴的两个端点的连线互相垂直,焦距为6.
分析:因为要求的是椭圆的标准方程,所以可以先设出椭圆的标准方程,再利用待定系数法求参数a,b,c.题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四 反思利用性质求椭圆的标准方程,通常采用待定系数法,而其关键是根据已知条件去构造关于参数的方程(组),利用解方程(组)求得参数.题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四求椭圆的离心率
【例3】 如图所示,椭圆的中心在原点,焦点F1,F2在x轴上,A,B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,求此椭圆的离心率.题型五题型一题型二题型三题型四反思求椭圆的离心率的常见思路:一是先求a,c,再计算e;二是依据条件中的关系,结合有关知识和a,b,c的关系,先构造关于e的方程(组),再求解.注意e的取值范围:0【例4】 已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点.
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于4?若存在,求出直线l的方程;若不存在,说明理由.题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四反思直线与椭圆之间有相交、相切、相离三种位置关系,即直线与椭圆有两个不同的公共点、唯一一个公共点、没有公共点.相应地,直线方程与椭圆方程联立组成的方程组有两组解、一组解、无解,消元后的一元二次方程对应的有Δ>0、Δ=0、Δ<0三种情况.题型五题型一题型二题型三题型四题型五(1)判断直线y=2x+6与椭圆是否有公共点? 因为Δ=62-4×2×5<0,
所以该方程组无解,即直线与椭圆没有公共点.题型一题型二题型三题型四题型五(2)设直线l的方程为y=x+m,A(x1,y1),B(x2,y2). 解得m=±2,验证知Δ>0成立,
所以直线l的方程为x-y+2=0或x-y-2=0. 题型一题型二题型三题型四题型五易错点 忽视焦点位置的不确定性致错 题型一题型二题型三题型四题型五
2.会根据椭圆的标准方程画出它的几何图形,并能根据几何性质解决一些简单问题.
3.理解直线与椭圆的位置关系.椭圆的简单几何性质 【做一做1】 椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的2倍,则m的值为( )答案:C 【做一做2】 椭圆x2+4y2=1的离心率为( )答案:A 【做一做3】 椭圆16x2+9y2=144的焦点坐标是 ,顶点坐标是 .?2.直线与椭圆的位置关系
剖析:(1)直线与椭圆有三种位置关系:
①相交——直线与椭圆有两个不同的公共点;
②相切——直线与椭圆有且只有一个公共点;
③相离——直线与椭圆没有公共点.
(2)直线与椭圆的位置关系的判断:
我们把直线与椭圆的位置关系问题转化为直线与椭圆的公共点问题,而直线与椭圆的公共点问题,又可以转化为它们的方程所组成的方程组的解的问题,而它们的方程所组成的方程组的解的问题又可以转化为一元二次方程解的问题,一元二次方程解的问题可以通过判别式来判断,因此,直线和椭圆的位置关系,可由相应的一元二次方程的判别式来判断.判断方法:将直线方程和椭圆的方程联立,消去一个未知数,得到一个一元二次方程,若Δ>0,则直线与椭圆相交;若Δ=0,则直线与椭圆相切;若Δ<0,则直线与椭圆相离.知识拓展由弦长公式可知,求弦长时可以不求出交点坐标,只需先将方程联立,整理成关于x(或y)的一元二次方程,再根据一元二次方程根与系数的关系求出x1+x2,x1x2(或y1+y2,y1y2),代入弦长公式即可.题型一题型二题型三题型四由方程求椭圆的几何性质题型五分析:先根据点在椭圆上,求出方程中实数m的值,再将方程化为标准形式,确定焦点位置及a,b,c的值,最后写出几何性质.题型一题型二题型三题型四题型五反思已知椭圆的方程讨论其几何性质时,应先把椭圆的方程化成标准形式,找准a与b,再正确地写出其相关性质.在求顶点坐标和焦点坐标时,应注意焦点所在的坐标轴.题型一题型二题型三题型四【变式训练1】 椭圆6x2+y2=6的长轴端点坐标为 ( )答案:D 题型五题型一题型二题型三题型四利用椭圆的几何性质求标准方程
【例2】 求适合下列条件的椭圆的标准方程:
(1)长轴长是6,
(2)焦点在x轴上,且一个焦点与短轴的两个端点的连线互相垂直,焦距为6.
分析:因为要求的是椭圆的标准方程,所以可以先设出椭圆的标准方程,再利用待定系数法求参数a,b,c.题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四 反思利用性质求椭圆的标准方程,通常采用待定系数法,而其关键是根据已知条件去构造关于参数的方程(组),利用解方程(组)求得参数.题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四求椭圆的离心率
【例3】 如图所示,椭圆的中心在原点,焦点F1,F2在x轴上,A,B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,求此椭圆的离心率.题型五题型一题型二题型三题型四反思求椭圆的离心率的常见思路:一是先求a,c,再计算e;二是依据条件中的关系,结合有关知识和a,b,c的关系,先构造关于e的方程(组),再求解.注意e的取值范围:0
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线l,使得直线l与椭圆C有公共点,且直线OA与l的距离等于4?若存在,求出直线l的方程;若不存在,说明理由.题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四题型五题型一题型二题型三题型四反思直线与椭圆之间有相交、相切、相离三种位置关系,即直线与椭圆有两个不同的公共点、唯一一个公共点、没有公共点.相应地,直线方程与椭圆方程联立组成的方程组有两组解、一组解、无解,消元后的一元二次方程对应的有Δ>0、Δ=0、Δ<0三种情况.题型五题型一题型二题型三题型四题型五(1)判断直线y=2x+6与椭圆是否有公共点? 因为Δ=62-4×2×5<0,
所以该方程组无解,即直线与椭圆没有公共点.题型一题型二题型三题型四题型五(2)设直线l的方程为y=x+m,A(x1,y1),B(x2,y2). 解得m=±2,验证知Δ>0成立,
所以直线l的方程为x-y+2=0或x-y-2=0. 题型一题型二题型三题型四题型五易错点 忽视焦点位置的不确定性致错 题型一题型二题型三题型四题型五
