2019-2020学年高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.4.2抛物线的简单几何性质(26张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程2.4.2抛物线的简单几何性质(26张) |  | |
| 格式 | zip | ||
| 文件大小 | 687.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-26 09:02:19 | ||
图片预览








文档简介
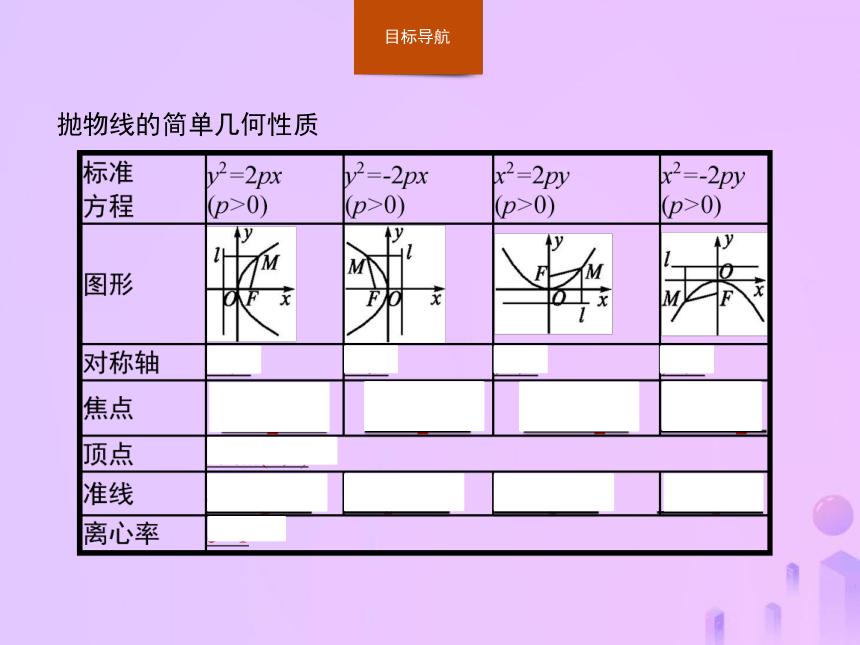
课件26张PPT。2.4.2 抛物线的简单几何性质抛物线的简单几何性质 知识拓展1.p的几何意义是焦点到准线的距离,抛物线不是双曲线的一支,抛物线不存在渐近线.【做一做1】 设A为抛物线y2=4x上一点,点B(1,0),且|AB|=1,则点A的横坐标的值为( )
A.-2 B.0
C.-2或0 D.-2或2
解析:由抛物线y2=4x的焦点为B(1,0),且|AB|=1,准线为x=-1,结合抛物线上的点到焦点的距离等于到准线的距离知,xA=0.
答案:B1.直线与抛物线的位置关系
剖析设直线l:y=kx+b,抛物线C:y2=2px(p>0),将直线方程与抛物线方程联立消元得,k2x2+(2kb-2p)x+b2=0,则有注意:直线与抛物线相交时,直线与抛物线不一定有两个公共点;直线与抛物线只有一个公共点时,直线与抛物线不一定相切,也有可能是相交,这时直线与抛物线的对称轴平行或重合.2.运用抛物线的定义解决问题
剖析由抛物线的定义可知,抛物线上的点到焦点的距离等于它到准线的距离,因此,涉及抛物线的焦点、过焦点的弦的问题,可以优先考虑利用抛物线的定义将点到焦点的距离与点到准线的距离相2.过焦点的直线交抛物线y2=2px(p>0)于A,B两点.
设A(x1,y1),B(x2,y2),则|AB|=x1+x2+p.题型一题型二题型三题型四抛物线的定义与性质的应用 分析:先确定抛物线方程的形式,再由条件用待定系数法求解.题型一题型二题型三题型四解法一:由已知条件可知抛物线的对称轴为x轴,
则可设抛物线的方程为y2=2px或y2=-2px(p>0).
∵抛物线的焦点到顶点的距离为5,
?
∴所求抛物线的方程为y2=20x或y2=-20x.
解法二:由已知条件可知抛物线的对称轴为x轴.
则设抛物线的方程为y2=mx(m≠0).
∵抛物线的焦点到顶点的距离为5,
?
故所求抛物线的方程为y2=20x或y2=-20x.题型一题型二题型三题型四反思顶点在原点,对称轴为x轴的抛物线方程可设为y2=mx(m≠0),当m>0时,开口向右;当m<0时,开口向左.顶点在原点,对称轴为y轴的抛物线方程可设为x2=my(m≠0),当m>0时,开口向上;当m<0时,开口向下.以上两种设法均可避开讨论抛物线的开口方向,焦点到准线的题型一题型二题型三题型四【变式训练1】 已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(4,-8),求它的标准方程.
解:由题意,可设抛物线的标准方程为y2=2px(p>0).
∵点M在抛物线上,
∴(-8)2=2p×4,解得p=8.
故所求抛物线的标准方程为y2=16x.题型一题型二题型三题型四与抛物线有关的定值问题
【例2】 已知AB是抛物线y2=2px(p>0)的过焦点F的一条弦.设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0).求证:题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四反思解决与抛物线有关的定值问题,常考虑利用抛物线的定义及一元二次方程根与系数的关系来解决,过焦点的弦长问题常结合抛物线的定义来解决.题型一题型二题型三题型四【变式训练2】 抛物线y2=2px(p>0)上有两动点A,B及一个定点M,F为焦点,且|AF|,|MF|,|BF|成等差数列(公差不为零).
(1)求证:线段AB的垂直平分线过定点Q;
(2)若|MF|=4,|OQ|=6(O为坐标原点),求抛物线的方程.题型一题型二题型三题型四题型一题型二题型三题型四与抛物线有关的最值问题 题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四反思1.具有定义背景的最值问题,可用定义转化为几何问题处理.
2.一般方法是由条件建立目标函数,然后利用求函数最值的方法求解最值.
3.常见问题类型及处理方法.(1)题型:一是求抛物线上一点到定直线的最小距离;二是求抛物线上一点到定点的距离的最值问题.(2)方法:一是利用数形结合;二是利用两点间距离公式并结合求函数最值的方法求解.
4.此类问题应注意抛物线的几何性质的应用,尤其是范围的应用.题型一题型二题型三题型四答案:D 题型一题型二题型三题型四易错辨析
易错点 忽略斜率不存在或二次项系数为零致错
【例4】 求过点P(0,1)且与抛物线y2=2x有且只有一个公共点的直线方程.题型一题型二题型三题型四题型一题型二题型三题型四反思一般地,点P在抛物线内,则过点P且和抛物线只有一个公共点的直线有一条;点P在抛物线上,则过点P且和抛物线只有一个公共点的直线有两条;点P在抛物线外,则过点P且和抛物线只有一个公共点的直线有三条.因此,在求过点P且与抛物线只有一个公共点的直线方程时要考虑周全,不要出现漏解的情况.另外,在求直线与抛物线的位置关系时,对消元后的方程不要忘记讨论二次项系数为零的情况.
A.-2 B.0
C.-2或0 D.-2或2
解析:由抛物线y2=4x的焦点为B(1,0),且|AB|=1,准线为x=-1,结合抛物线上的点到焦点的距离等于到准线的距离知,xA=0.
答案:B1.直线与抛物线的位置关系
剖析设直线l:y=kx+b,抛物线C:y2=2px(p>0),将直线方程与抛物线方程联立消元得,k2x2+(2kb-2p)x+b2=0,则有注意:直线与抛物线相交时,直线与抛物线不一定有两个公共点;直线与抛物线只有一个公共点时,直线与抛物线不一定相切,也有可能是相交,这时直线与抛物线的对称轴平行或重合.2.运用抛物线的定义解决问题
剖析由抛物线的定义可知,抛物线上的点到焦点的距离等于它到准线的距离,因此,涉及抛物线的焦点、过焦点的弦的问题,可以优先考虑利用抛物线的定义将点到焦点的距离与点到准线的距离相2.过焦点的直线交抛物线y2=2px(p>0)于A,B两点.
设A(x1,y1),B(x2,y2),则|AB|=x1+x2+p.题型一题型二题型三题型四抛物线的定义与性质的应用 分析:先确定抛物线方程的形式,再由条件用待定系数法求解.题型一题型二题型三题型四解法一:由已知条件可知抛物线的对称轴为x轴,
则可设抛物线的方程为y2=2px或y2=-2px(p>0).
∵抛物线的焦点到顶点的距离为5,
?
∴所求抛物线的方程为y2=20x或y2=-20x.
解法二:由已知条件可知抛物线的对称轴为x轴.
则设抛物线的方程为y2=mx(m≠0).
∵抛物线的焦点到顶点的距离为5,
?
故所求抛物线的方程为y2=20x或y2=-20x.题型一题型二题型三题型四反思顶点在原点,对称轴为x轴的抛物线方程可设为y2=mx(m≠0),当m>0时,开口向右;当m<0时,开口向左.顶点在原点,对称轴为y轴的抛物线方程可设为x2=my(m≠0),当m>0时,开口向上;当m<0时,开口向下.以上两种设法均可避开讨论抛物线的开口方向,焦点到准线的题型一题型二题型三题型四【变式训练1】 已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(4,-8),求它的标准方程.
解:由题意,可设抛物线的标准方程为y2=2px(p>0).
∵点M在抛物线上,
∴(-8)2=2p×4,解得p=8.
故所求抛物线的标准方程为y2=16x.题型一题型二题型三题型四与抛物线有关的定值问题
【例2】 已知AB是抛物线y2=2px(p>0)的过焦点F的一条弦.设A(x1,y1),B(x2,y2),AB的中点为M(x0,y0).求证:题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四反思解决与抛物线有关的定值问题,常考虑利用抛物线的定义及一元二次方程根与系数的关系来解决,过焦点的弦长问题常结合抛物线的定义来解决.题型一题型二题型三题型四【变式训练2】 抛物线y2=2px(p>0)上有两动点A,B及一个定点M,F为焦点,且|AF|,|MF|,|BF|成等差数列(公差不为零).
(1)求证:线段AB的垂直平分线过定点Q;
(2)若|MF|=4,|OQ|=6(O为坐标原点),求抛物线的方程.题型一题型二题型三题型四题型一题型二题型三题型四与抛物线有关的最值问题 题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四反思1.具有定义背景的最值问题,可用定义转化为几何问题处理.
2.一般方法是由条件建立目标函数,然后利用求函数最值的方法求解最值.
3.常见问题类型及处理方法.(1)题型:一是求抛物线上一点到定直线的最小距离;二是求抛物线上一点到定点的距离的最值问题.(2)方法:一是利用数形结合;二是利用两点间距离公式并结合求函数最值的方法求解.
4.此类问题应注意抛物线的几何性质的应用,尤其是范围的应用.题型一题型二题型三题型四答案:D 题型一题型二题型三题型四易错辨析
易错点 忽略斜率不存在或二次项系数为零致错
【例4】 求过点P(0,1)且与抛物线y2=2x有且只有一个公共点的直线方程.题型一题型二题型三题型四题型一题型二题型三题型四反思一般地,点P在抛物线内,则过点P且和抛物线只有一个公共点的直线有一条;点P在抛物线上,则过点P且和抛物线只有一个公共点的直线有两条;点P在抛物线外,则过点P且和抛物线只有一个公共点的直线有三条.因此,在求过点P且与抛物线只有一个公共点的直线方程时要考虑周全,不要出现漏解的情况.另外,在求直线与抛物线的位置关系时,对消元后的方程不要忘记讨论二次项系数为零的情况.
