2019-2020学年高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程本章整合(52张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版选修2-1课件:第二章圆锥曲线与方程本章整合(52张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-26 09:01:13 | ||
图片预览








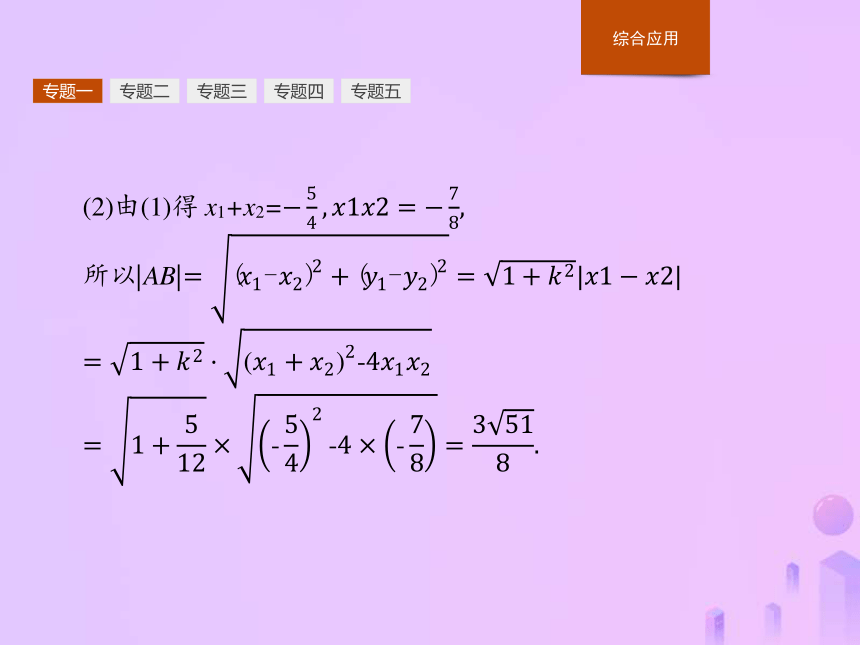



文档简介
课件52张PPT。本章整合圆
锥
曲
线圆
锥
曲
线圆
锥
曲
线专题一专题二专题三专题四专题一 直线与圆锥曲线的位置关系
1.已知直线l的方程为Ax+By+C=0,圆锥曲线M的方程为f(x,y)=0.
?
?
如消去y后,得ax2+bx+c=0.
(1)若a=0,当圆锥曲线M是双曲线时,直线l与双曲线的渐近线平行;当圆锥曲线M是抛物线时,直线l与抛物线的对称轴平行(或重合).
(2)若a≠0,设Δ=b2-4ac.
当Δ>0时,直线和圆锥曲线M相交于不同的两点;
当Δ=0时,直线和圆锥曲线M相切于一点;
当Δ<0时,直线和圆锥曲线M没有公共点.专题五专题一专题二专题三专题四2.直线与圆锥曲线的位置关系,涉及函数、方程、不等式、平面几何等诸多方面的知识,形成了求轨迹、最值、对称、取值范围、线段的长度等多种问题.解决此类问题应注意数形结合,以形辅数的方法,还要多结合圆锥曲线的定义、根与系数的关系以及“点差法”等.这些问题也是以往高考的重点和热点,高考中,大多以解答题的形式出现而且难度较大.专题五专题一专题二专题三专题四专题五(1)求直线l的方程;
(2)求弦AB的长度.
解:(1)若直线l的斜率不存在,则其方程为x=-1,显然不满足|EA|=2|EB|.故直线l的斜率一定存在,设为k,则l的方程为y=k(x+1).Δ=(8k2)2-4(4k2+1)(4k2-4)=48k2+16>0.
设A(x1,y1),B(x2,y2),专题一专题二专题三专题四专题五因为|EA|=2|EB|,所以x1+2x2=-3, 专题一专题二专题三专题四专题五专题一专题二专题三专题四专题二 动点的轨迹方程
1.求轨迹方程的步骤:建系、设点、列式、化简、确定点的范围.
2.求轨迹方程的常用方法:
(1)直接法:直接利用条件建立x,y之间的关系式F(x,y)=0,注意求谁设谁.
(2)待定系数法:已知所求曲线的类型,求曲线方程,先根据条件设出所求曲线的含参方程,再由条件确定其待定系数.
(3)定义法:先根据条件得出动点的轨迹是某种已知曲线,再由曲线的定义直接写出动点的轨迹方程.
(4)相关点法:动点P(x,y)随另一动点Q(x0,y0)的变化而变化,并且Q(x0,y0)又在某已知曲线上,则可先用含x,y的代数式表示x0,y0,再将x0,y0代入已知曲线得到要求的轨迹方程.专题五专题一专题二专题三专题四应用△ABC的一边的两个顶点分别为B(-a,0),C(a,0)(a>0),另两边的斜率之积等于m(m≠0).求顶点A的轨迹方程,并且根据m的取值情况讨论其轨迹.当m>0时,轨迹是中心在原点,焦点在x轴上的双曲线(两顶点除外);
当m<0,且m≠-1时,轨迹是中心在原点,以坐标轴为对称轴的椭圆(除去与x轴的两个交点),其中当-1当m<-1时,椭圆的焦点在y轴上;
当m=-1时,轨迹是圆心在原点,半径为a的圆(除去与x轴的两个交点).专题五专题一专题二专题三专题四专题三 与圆锥曲线有关的最值和范围问题
与圆锥曲线有关的最值和范围问题的讨论常用以下方法解决:
1.结合定义利用图形中几何量之间的大小关系.
2.不等式(组)求解法:根据题意结合图形(如点在曲线内等)列出所讨论的参数适合的不等式(组),通过解不等式(组)得出参数的变化范围.
3.函数值域求解法:把所讨论的参数作为一个函数、另一个适当的参数作为自变量来表示这个函数,通过讨论函数的值域来求参数的变化范围.
4.利用基本不等式:基本不等式的应用,往往需要创造条件,并进行巧妙的构思.
5.构造一个一元二次方程,利用判别式Δ≥0来求解.专题五专题一专题二专题三专题四应用 专题五专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五专题一专题二专题三专题四专题四 定点、定值问题的求解策略
1.定点问题的求解策略
(1)探索直线过定点时,可设出直线方程为y=kx+b,然后利用条件建立b,k数量关系进行消元,借助于直线方程找出定点;
(2)从特殊情况入手,先探求定点,再证明一般情况.专题五专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五应用1已知抛物线y2=2px(p>0)的准线与x轴的交点坐标是(-4,0).
(1)求抛物线方程;
(2)求定点M,使过点M的直线l与抛物线交于B,C两点(异于原点),且以BC为直径的圆恰好经过原点.
解:(1)依题意,准线方程为x=-4,专题一专题二专题三专题四专题五(2)当直线l的斜率存在时,设其方程为y=kx+b,显然k≠0,b≠0.
设B(x1,y1),C(x2,y2),因为以BC为直径的圆恰好经过原点,此时直线l的方程为y=k(x-16),必过定点(16,0).
当直线l的斜率不存在时,直线x=16与抛物线y2=16x相交于B(16,16),C(16,-16)或B(16,-16),C(16,16),专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五专题五 探索性问题的求解策略
圆锥曲线中的探索性问题是高考命题的热点,主要以解答题的形式出现,难度较大,一般作为压轴题.解决这类问题往往采用“假设反证法”或“假设检验法”,也可先用特殊情况得到所求值,再给出一般性的证明.考查的知识点多,能力要求高,尤其是运算变形能力,同时着重考查学生的分析问题与解决综合问题的能力.专题一专题二专题三专题四专题五提示:(1)将直线方程与双曲线方程联立,利用弦长公式求解即可;(2)假设存在,根据已知条件进行推理,看推导结果是否与已知条件相矛盾.专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五(2)假设存在实数a,
使得以PQ为直径的圆经过坐标原点O,则由OP⊥OQ,
得x1x2+y1y2=0,从而得a2=-2,
这与实数的性质矛盾,故不存在实数a,
使得以PQ为直径的圆过坐标原点.13123456789101112141516解析:因为椭圆C的一个焦点为(2,0),所以其焦点在x轴上,c=2, 答案:C 13123456789101112141516答案:D 13123456789101112141516答案:A 13123456789101112141516所以|MN|=3.
答案:B131234567891011121415165(2018全国1高考)设抛物线C:y2=4x的焦点为F,过点(-2,0)且斜率 A.5 B.6 C.7 D.8 答案:D 1312345678910111214151613123456789101112141516?答案:C 13123456789101112141516解析:由c2=a2+b2=4,得c=2,所以点F的坐标为(2,0). ?13123456789101112141516答案:C 13123456789101112141516解析:由题意可知抛物线的焦点F(1,0),准线l的方程为x=-1,可得直 答案:C 1312345678910111214151610(2017全国1高考)已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为( )
A.16 B.14 C.12 D.10
解析:方法一:由题意,易知直线l1,l2斜率不存在时,不合题意.
设直线l1方程为y=k1(x-1),131234567891011121415161312345678910111214151613123456789101112141516答案:A 13123456789101112141516解析:由题意,可知当点M为短轴的端点时,∠AMB最大.
当0答案:A1312345678910111214151612(2018全国3高考)已知点M(-1,1)和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B两点,若∠AMB=90°,则k= .?
解析:设直线AB:x=my+1,=(m2+1)y1y2+(2m-1)(y1+y2)+5
=-4(m2+1)+(2m-1)4m+5=4m2-4m+1=0.答案:2 13123456789101112141516解析:如图所示,由题意可得|OA|=a,|AN|=|AM|=b, 1312345678910111214151613123456789101112141516(1)当l与x轴垂直时,求直线AM的方程;
(2)设O为坐标原点,证明:∠OMA=∠OMB.
(1)解:由已知得F(1,0),l的方程为x=1.13123456789101112141516(2)证明:当l与x轴重合时,∠OMA=∠OMB=0°,
当l与x轴垂直时,OM为AB的垂直平分线,
所以∠OMA=∠OMB.
当l与x轴不重合也不垂直时,设l的方程为y=k(x-1)(k≠0),
A(x1,y1),B(x2,y2),13123456789101112141516从而kMA+kMB=0,故MA,MB的倾斜角互补,
所以∠OMA=∠OMB.
综上,∠OMA=∠OMB.1312345678910111214151615(2018全国2高考)设抛物线C:y2=4x的焦点为F,过F且斜率为k(k>0)的直线l与C交于A,B两点,|AB|=8.
(1)求l的方程.
(2)求过点A,B且与C的准线相切的圆的方程.
解:(1)由题意得F(1,0),l的方程为y=k(x-1)(k>0).
设A(x1,y1),B(x2,y2).因此l的方程为y=x-1. 13123456789101112141516(2)由(1)得AB的中点坐标为(3,2),
所以AB的垂直平分线方程为y-2=-(x-3),即y=-x+5.
设所求圆的圆心坐标为(x0,y0),因此所求圆的方程为(x-3)2+(y-2)2=16或(x-11)2+(y+6)2=144.13123456789101112141516(1)求直线AB的斜率;
(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM⊥BM,求直线AB的方程.解:(1)设A(x1,y1),B(x2,y2), 13123456789101112141516解得m=7.
所以直线AB的方程为y=x+7.
锥
曲
线圆
锥
曲
线圆
锥
曲
线专题一专题二专题三专题四专题一 直线与圆锥曲线的位置关系
1.已知直线l的方程为Ax+By+C=0,圆锥曲线M的方程为f(x,y)=0.
?
?
如消去y后,得ax2+bx+c=0.
(1)若a=0,当圆锥曲线M是双曲线时,直线l与双曲线的渐近线平行;当圆锥曲线M是抛物线时,直线l与抛物线的对称轴平行(或重合).
(2)若a≠0,设Δ=b2-4ac.
当Δ>0时,直线和圆锥曲线M相交于不同的两点;
当Δ=0时,直线和圆锥曲线M相切于一点;
当Δ<0时,直线和圆锥曲线M没有公共点.专题五专题一专题二专题三专题四2.直线与圆锥曲线的位置关系,涉及函数、方程、不等式、平面几何等诸多方面的知识,形成了求轨迹、最值、对称、取值范围、线段的长度等多种问题.解决此类问题应注意数形结合,以形辅数的方法,还要多结合圆锥曲线的定义、根与系数的关系以及“点差法”等.这些问题也是以往高考的重点和热点,高考中,大多以解答题的形式出现而且难度较大.专题五专题一专题二专题三专题四专题五(1)求直线l的方程;
(2)求弦AB的长度.
解:(1)若直线l的斜率不存在,则其方程为x=-1,显然不满足|EA|=2|EB|.故直线l的斜率一定存在,设为k,则l的方程为y=k(x+1).Δ=(8k2)2-4(4k2+1)(4k2-4)=48k2+16>0.
设A(x1,y1),B(x2,y2),专题一专题二专题三专题四专题五因为|EA|=2|EB|,所以x1+2x2=-3, 专题一专题二专题三专题四专题五专题一专题二专题三专题四专题二 动点的轨迹方程
1.求轨迹方程的步骤:建系、设点、列式、化简、确定点的范围.
2.求轨迹方程的常用方法:
(1)直接法:直接利用条件建立x,y之间的关系式F(x,y)=0,注意求谁设谁.
(2)待定系数法:已知所求曲线的类型,求曲线方程,先根据条件设出所求曲线的含参方程,再由条件确定其待定系数.
(3)定义法:先根据条件得出动点的轨迹是某种已知曲线,再由曲线的定义直接写出动点的轨迹方程.
(4)相关点法:动点P(x,y)随另一动点Q(x0,y0)的变化而变化,并且Q(x0,y0)又在某已知曲线上,则可先用含x,y的代数式表示x0,y0,再将x0,y0代入已知曲线得到要求的轨迹方程.专题五专题一专题二专题三专题四应用△ABC的一边的两个顶点分别为B(-a,0),C(a,0)(a>0),另两边的斜率之积等于m(m≠0).求顶点A的轨迹方程,并且根据m的取值情况讨论其轨迹.当m>0时,轨迹是中心在原点,焦点在x轴上的双曲线(两顶点除外);
当m<0,且m≠-1时,轨迹是中心在原点,以坐标轴为对称轴的椭圆(除去与x轴的两个交点),其中当-1
当m=-1时,轨迹是圆心在原点,半径为a的圆(除去与x轴的两个交点).专题五专题一专题二专题三专题四专题三 与圆锥曲线有关的最值和范围问题
与圆锥曲线有关的最值和范围问题的讨论常用以下方法解决:
1.结合定义利用图形中几何量之间的大小关系.
2.不等式(组)求解法:根据题意结合图形(如点在曲线内等)列出所讨论的参数适合的不等式(组),通过解不等式(组)得出参数的变化范围.
3.函数值域求解法:把所讨论的参数作为一个函数、另一个适当的参数作为自变量来表示这个函数,通过讨论函数的值域来求参数的变化范围.
4.利用基本不等式:基本不等式的应用,往往需要创造条件,并进行巧妙的构思.
5.构造一个一元二次方程,利用判别式Δ≥0来求解.专题五专题一专题二专题三专题四应用 专题五专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五专题一专题二专题三专题四专题四 定点、定值问题的求解策略
1.定点问题的求解策略
(1)探索直线过定点时,可设出直线方程为y=kx+b,然后利用条件建立b,k数量关系进行消元,借助于直线方程找出定点;
(2)从特殊情况入手,先探求定点,再证明一般情况.专题五专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五应用1已知抛物线y2=2px(p>0)的准线与x轴的交点坐标是(-4,0).
(1)求抛物线方程;
(2)求定点M,使过点M的直线l与抛物线交于B,C两点(异于原点),且以BC为直径的圆恰好经过原点.
解:(1)依题意,准线方程为x=-4,专题一专题二专题三专题四专题五(2)当直线l的斜率存在时,设其方程为y=kx+b,显然k≠0,b≠0.
设B(x1,y1),C(x2,y2),因为以BC为直径的圆恰好经过原点,此时直线l的方程为y=k(x-16),必过定点(16,0).
当直线l的斜率不存在时,直线x=16与抛物线y2=16x相交于B(16,16),C(16,-16)或B(16,-16),C(16,16),专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五专题五 探索性问题的求解策略
圆锥曲线中的探索性问题是高考命题的热点,主要以解答题的形式出现,难度较大,一般作为压轴题.解决这类问题往往采用“假设反证法”或“假设检验法”,也可先用特殊情况得到所求值,再给出一般性的证明.考查的知识点多,能力要求高,尤其是运算变形能力,同时着重考查学生的分析问题与解决综合问题的能力.专题一专题二专题三专题四专题五提示:(1)将直线方程与双曲线方程联立,利用弦长公式求解即可;(2)假设存在,根据已知条件进行推理,看推导结果是否与已知条件相矛盾.专题一专题二专题三专题四专题五专题一专题二专题三专题四专题五(2)假设存在实数a,
使得以PQ为直径的圆经过坐标原点O,则由OP⊥OQ,
得x1x2+y1y2=0,从而得a2=-2,
这与实数的性质矛盾,故不存在实数a,
使得以PQ为直径的圆过坐标原点.13123456789101112141516解析:因为椭圆C的一个焦点为(2,0),所以其焦点在x轴上,c=2, 答案:C 13123456789101112141516答案:D 13123456789101112141516答案:A 13123456789101112141516所以|MN|=3.
答案:B131234567891011121415165(2018全国1高考)设抛物线C:y2=4x的焦点为F,过点(-2,0)且斜率 A.5 B.6 C.7 D.8 答案:D 1312345678910111214151613123456789101112141516?答案:C 13123456789101112141516解析:由c2=a2+b2=4,得c=2,所以点F的坐标为(2,0). ?13123456789101112141516答案:C 13123456789101112141516解析:由题意可知抛物线的焦点F(1,0),准线l的方程为x=-1,可得直 答案:C 1312345678910111214151610(2017全国1高考)已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1,l2,直线l1与C交于A,B两点,直线l2与C交于D,E两点,则|AB|+|DE|的最小值为( )
A.16 B.14 C.12 D.10
解析:方法一:由题意,易知直线l1,l2斜率不存在时,不合题意.
设直线l1方程为y=k1(x-1),131234567891011121415161312345678910111214151613123456789101112141516答案:A 13123456789101112141516解析:由题意,可知当点M为短轴的端点时,∠AMB最大.
当0
解析:设直线AB:x=my+1,=(m2+1)y1y2+(2m-1)(y1+y2)+5
=-4(m2+1)+(2m-1)4m+5=4m2-4m+1=0.答案:2 13123456789101112141516解析:如图所示,由题意可得|OA|=a,|AN|=|AM|=b, 1312345678910111214151613123456789101112141516(1)当l与x轴垂直时,求直线AM的方程;
(2)设O为坐标原点,证明:∠OMA=∠OMB.
(1)解:由已知得F(1,0),l的方程为x=1.13123456789101112141516(2)证明:当l与x轴重合时,∠OMA=∠OMB=0°,
当l与x轴垂直时,OM为AB的垂直平分线,
所以∠OMA=∠OMB.
当l与x轴不重合也不垂直时,设l的方程为y=k(x-1)(k≠0),
A(x1,y1),B(x2,y2),13123456789101112141516从而kMA+kMB=0,故MA,MB的倾斜角互补,
所以∠OMA=∠OMB.
综上,∠OMA=∠OMB.1312345678910111214151615(2018全国2高考)设抛物线C:y2=4x的焦点为F,过F且斜率为k(k>0)的直线l与C交于A,B两点,|AB|=8.
(1)求l的方程.
(2)求过点A,B且与C的准线相切的圆的方程.
解:(1)由题意得F(1,0),l的方程为y=k(x-1)(k>0).
设A(x1,y1),B(x2,y2).因此l的方程为y=x-1. 13123456789101112141516(2)由(1)得AB的中点坐标为(3,2),
所以AB的垂直平分线方程为y-2=-(x-3),即y=-x+5.
设所求圆的圆心坐标为(x0,y0),因此所求圆的方程为(x-3)2+(y-2)2=16或(x-11)2+(y+6)2=144.13123456789101112141516(1)求直线AB的斜率;
(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM⊥BM,求直线AB的方程.解:(1)设A(x1,y1),B(x2,y2), 13123456789101112141516解得m=7.
所以直线AB的方程为y=x+7.
