2019-2020学年高中数学新人教A版选修2-1课件:第三章空间向量与立体几何3.2.2用向量方法解决垂直问题课(22张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版选修2-1课件:第三章空间向量与立体几何3.2.2用向量方法解决垂直问题课(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 572.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-26 00:00:00 | ||
图片预览








文档简介
课件20张PPT。第2课时 用向量方法解决垂直问题1.理解线面的位置关系与向量的联系.
2.能用向量语言表述线线、线面、面面的垂直关系.空间中垂直关系的向量表示
设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为u,v,则
(1)线线垂直:l⊥m?a⊥b?a·b=0;
(2)线面垂直:l⊥α?a∥u?a=ku(k∈R);
(3)面面垂直:α⊥β?u⊥v?u·v=0.【做一做1】 设直线l1,l2的方向向量分别为a=(1,2,-2),b=(-2,3,m),若l1⊥l2,则m=( )
A.1 B.2 C.3 D.4
解析:∵l1⊥l2,∴a⊥b.
∴a·b=-2+6-2m=0,∴m=2.
答案:B
【做一做2】 若直线l的方向向量为a=(1,0,2),平面α的法向量为n=(-2,0,-4),则( )
A.l∥α B.l⊥α
C.l?α D.l与α斜交
解析:∵n=-2a,∴n∥a.∴l⊥α.
答案:B应用向量方法证明垂直问题
剖析:1.线线垂直
设直线l1,l2的方向向量分别是a,b,则要证明l1⊥l2,只需证明a⊥b,即a·b=0.
2.线面垂直
(1)设直线l的方向向量是a,平面α的法向量是u,则要证l⊥α,只需证明a∥u,即a=ku(k∈R).
(2)根据线面垂直的判定定理,转化为直线与平面内的两条相交直线垂直,即设a,b是在平面α内(或与平面α平行)的两条直线的方向向量,且a与b不平行,直线l的方向向量为c,则l⊥α?c⊥a,且c⊥b?a·c=b·c=0.
3.面面垂直
(1)根据面面垂直的判定定理转化为证明相应的线面垂直、线线垂直.
(2)证明两个平面的法向量互相垂直.题型一题型二题型三证明线线垂直 题型一题型二题型三反思证明线线垂直,只需证明两条直线的方向向量的数量积为0,可以建立空间直角坐标系,用坐标运算来解决,也可以利用向量间的几何关系来证明.题型一题型二题型三【变式训练1】 在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是AB,BC上的动点,且AE=BF,求证:A1F⊥C1E.题型一题型二题型三证明线面垂直
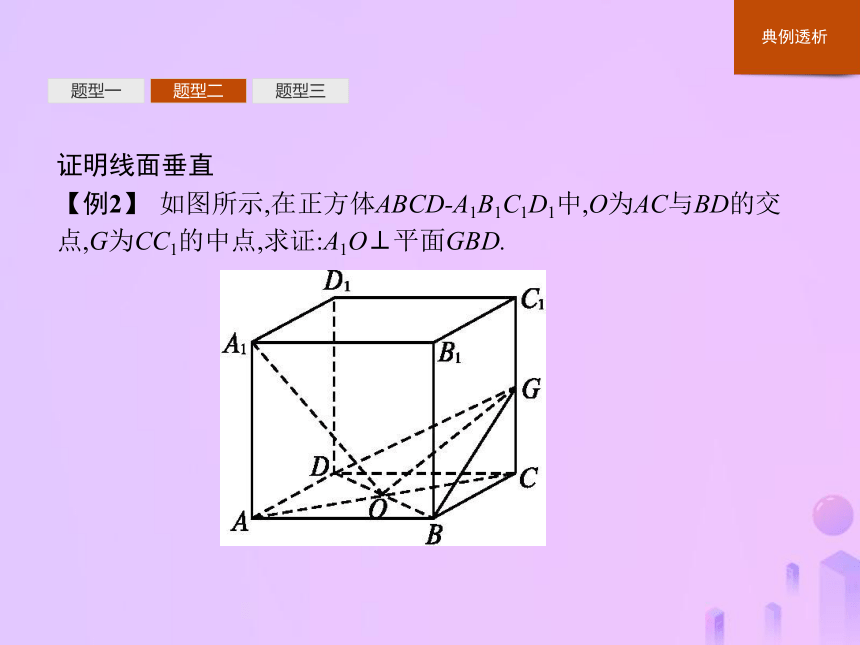
【例2】 如图所示,在正方体ABCD-A1B1C1D1中,O为AC与BD的交点,G为CC1的中点,求证:A1O⊥平面GBD.题型一题型二题型三题型一题型二题型三题型一题型二题型三题型一题型二题型三反思利用向量方法证明线面垂直的方法
(1)利用基向量:先选取基向量,用基向量表示直线所在的向量,在平面内找出两个不共线的向量,也用基向量表示,再根据数量积运算律分别证明直线所在向量与两个不共线向量的数量积均为零,从而证得结论.
(2)坐标法:先建立空间直角坐标系,求出直线方向向量的坐标以及平面内两个不共线向量的坐标,再根据数量积的坐标运算法则证明直线的方向向量与两个不共线向量的数量积均为零,从而证得结论.
(3)利用法向量:先建立空间直角坐标系,求出直线方向向量的坐标以及平面法向量的坐标,再说明直线方向向量与平面法向量共线,从而证得结论.题型一题型二题型三【变式训练2】 在长方体ABCD-A1B1C1D1中,E,F分别是棱BC,
CC1上的点,CF=AB=2CE,AB∶AD∶AA1=1∶2∶4.求证:AF⊥平面A1ED.题型一题型二题型三题型一题型二题型三证明面面垂直 分析:因为FA⊥平面ABCD,
所以可以以点A为坐标原点建立空间直角坐标系.题型一题型二题型三反思证明面面垂直通常有两种方法,一是利用面面垂直的判定定理转化为线面垂直、线线垂直去证明;二是证明两个平面的法向量互相垂直.题型一题型二题型三【变式训练3】 如图所示,在六面体ABCD-A1B1C1D1中,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.
求证:(1)A1C1与AC共面,B1D1与BD共面;
(2)平面A1ACC1⊥平面B1BDD1.题型一题型二题型三证明:(1)如图所示,以D为坐标原点,DA,DC,DD1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,题型一题型二题型三
2.能用向量语言表述线线、线面、面面的垂直关系.空间中垂直关系的向量表示
设直线l,m的方向向量分别为a,b,平面α,β的法向量分别为u,v,则
(1)线线垂直:l⊥m?a⊥b?a·b=0;
(2)线面垂直:l⊥α?a∥u?a=ku(k∈R);
(3)面面垂直:α⊥β?u⊥v?u·v=0.【做一做1】 设直线l1,l2的方向向量分别为a=(1,2,-2),b=(-2,3,m),若l1⊥l2,则m=( )
A.1 B.2 C.3 D.4
解析:∵l1⊥l2,∴a⊥b.
∴a·b=-2+6-2m=0,∴m=2.
答案:B
【做一做2】 若直线l的方向向量为a=(1,0,2),平面α的法向量为n=(-2,0,-4),则( )
A.l∥α B.l⊥α
C.l?α D.l与α斜交
解析:∵n=-2a,∴n∥a.∴l⊥α.
答案:B应用向量方法证明垂直问题
剖析:1.线线垂直
设直线l1,l2的方向向量分别是a,b,则要证明l1⊥l2,只需证明a⊥b,即a·b=0.
2.线面垂直
(1)设直线l的方向向量是a,平面α的法向量是u,则要证l⊥α,只需证明a∥u,即a=ku(k∈R).
(2)根据线面垂直的判定定理,转化为直线与平面内的两条相交直线垂直,即设a,b是在平面α内(或与平面α平行)的两条直线的方向向量,且a与b不平行,直线l的方向向量为c,则l⊥α?c⊥a,且c⊥b?a·c=b·c=0.
3.面面垂直
(1)根据面面垂直的判定定理转化为证明相应的线面垂直、线线垂直.
(2)证明两个平面的法向量互相垂直.题型一题型二题型三证明线线垂直 题型一题型二题型三反思证明线线垂直,只需证明两条直线的方向向量的数量积为0,可以建立空间直角坐标系,用坐标运算来解决,也可以利用向量间的几何关系来证明.题型一题型二题型三【变式训练1】 在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是AB,BC上的动点,且AE=BF,求证:A1F⊥C1E.题型一题型二题型三证明线面垂直
【例2】 如图所示,在正方体ABCD-A1B1C1D1中,O为AC与BD的交点,G为CC1的中点,求证:A1O⊥平面GBD.题型一题型二题型三题型一题型二题型三题型一题型二题型三题型一题型二题型三反思利用向量方法证明线面垂直的方法
(1)利用基向量:先选取基向量,用基向量表示直线所在的向量,在平面内找出两个不共线的向量,也用基向量表示,再根据数量积运算律分别证明直线所在向量与两个不共线向量的数量积均为零,从而证得结论.
(2)坐标法:先建立空间直角坐标系,求出直线方向向量的坐标以及平面内两个不共线向量的坐标,再根据数量积的坐标运算法则证明直线的方向向量与两个不共线向量的数量积均为零,从而证得结论.
(3)利用法向量:先建立空间直角坐标系,求出直线方向向量的坐标以及平面法向量的坐标,再说明直线方向向量与平面法向量共线,从而证得结论.题型一题型二题型三【变式训练2】 在长方体ABCD-A1B1C1D1中,E,F分别是棱BC,
CC1上的点,CF=AB=2CE,AB∶AD∶AA1=1∶2∶4.求证:AF⊥平面A1ED.题型一题型二题型三题型一题型二题型三证明面面垂直 分析:因为FA⊥平面ABCD,
所以可以以点A为坐标原点建立空间直角坐标系.题型一题型二题型三反思证明面面垂直通常有两种方法,一是利用面面垂直的判定定理转化为线面垂直、线线垂直去证明;二是证明两个平面的法向量互相垂直.题型一题型二题型三【变式训练3】 如图所示,在六面体ABCD-A1B1C1D1中,四边形ABCD是边长为2的正方形,四边形A1B1C1D1是边长为1的正方形,DD1⊥平面A1B1C1D1,DD1⊥平面ABCD,DD1=2.
求证:(1)A1C1与AC共面,B1D1与BD共面;
(2)平面A1ACC1⊥平面B1BDD1.题型一题型二题型三证明:(1)如图所示,以D为坐标原点,DA,DC,DD1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系,题型一题型二题型三
