2019-2020学年高中数学新人教A版选修2-1课件:第三章空间向量与立体几何3.2.3用向量方法求空间中的角(27张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版选修2-1课件:第三章空间向量与立体几何3.2.3用向量方法求空间中的角(27张) |

|
|
| 格式 | zip | ||
| 文件大小 | 870.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-26 00:00:00 | ||
图片预览







文档简介
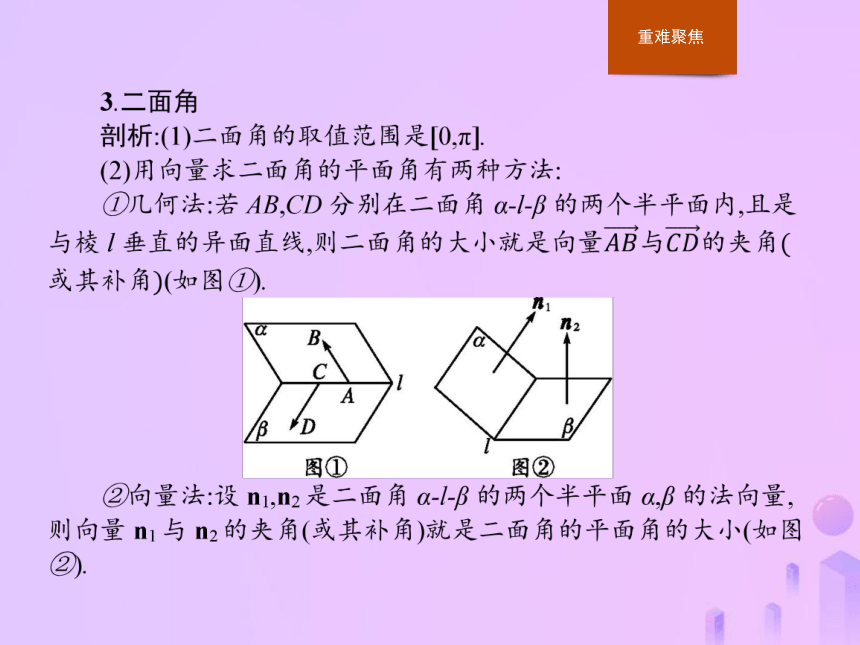
课件27张PPT。第3课时 用向量方法求空间中的角1.理解直线与平面所成角的概念.
2.能用向量方法解决线线、线面、面面夹角的问题.
3.了解向量方法在研究几何问题中的作用.【做一做1】 若异面直线l1的方向向量与l2的方向向量的夹角为150°,则l1与l2所成的角等于( )
A.30° B.150°
C.30°或150° D.以上均错
解析:由异面直线夹角定义知,异面直线夹角范围是(0°,90°].
答案:A【做一做2】 若直线l的方向向量与平面α的法向量的夹角等于120°,则直线l与平面α所成的角等于( )
A.120° B.60°
C.150° D.30°
解析:因为直线l的方向向量与平面α的法向量的夹角等于120°,所以它们所在直线的夹角为60°,则直线l与平面α所成的角等于90°-60°=30°.
答案:D
【做一做3】 若平面α的一个法向量为n1=(1,0,1),平面β的一个法向量是n2=(-3,1,3),则平面α与β所成的角等于( )
A.30° B.45° C.60° D.90°
解析:因为n1·n2=0,所以α⊥β,即平面α与β所成的角等于90°.
答案:D题型一题型二题型三题型四求异面直线所成的角
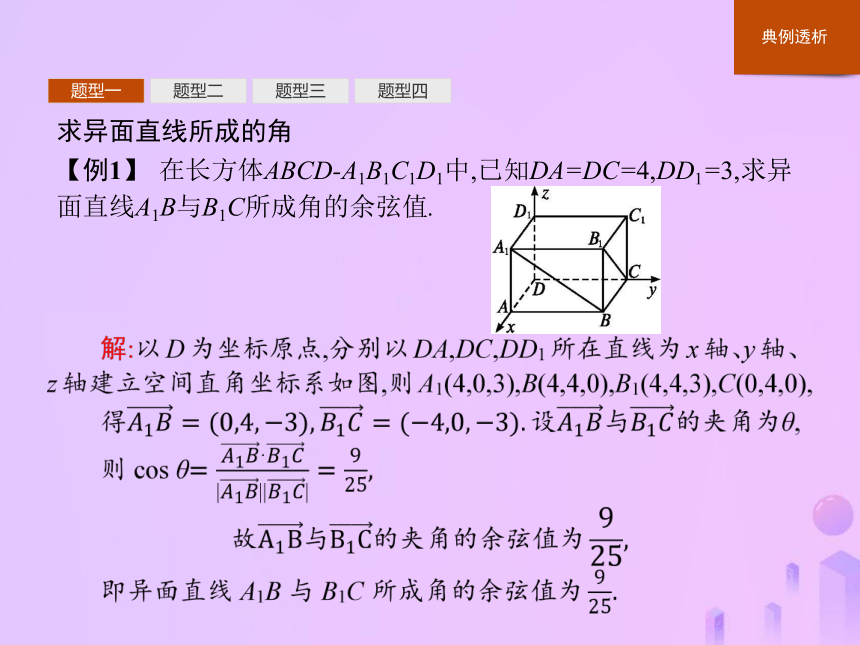
【例1】 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求异面直线A1B与B1C所成角的余弦值.题型一题型二题型三题型四反思建立空间直角坐标系,要充分利用题目中的垂直关系.利用向量法求两异面直线所成角的计算思路简便,但是要注意角的范围.题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四求直线与平面所成的角
【例2】 在棱长为1的正方体ABCD-A1B1C1D1中,在侧棱CC1上求一点P,使得直线AP与平面BDD1B1所成的角的正切值为3 .
解:如图,以D为坐标原点,分别以DA,DC,DD1所在直线为x轴、y轴、z轴建立空间直角坐标系.题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四【变式训练2】 在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD,PD=DC,E是PC的中点,求EB与平面ABCD夹角的余弦值.题型一题型二题型三题型四求二面角
【例3】 如图,四棱锥P-ABCD的底面ABCD是菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
(1)求证:AE⊥PD;
(2)若PA=AB=2,求二面角E-AF-C的余弦值.题型一题型二题型三题型四(1)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.
又BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE?平面ABCD,
所以PA⊥AE.
而PA?平面PAD,AD?平面PAD,且PA∩AD=A,所以AE⊥平面PAD.
又PD?平面PAD,所以AE⊥PD.题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四反思用几何法求二面角,往往需要作出其平面角,这是几何中的难点之一;而用向量法求解二面角无须作出二面角的平面角,只需求出平面的法向量,经过简单运算即可.题型一题型二题型三题型四【变式训练3】 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四易错辨析
易错点 对向量法求线面角的原理不理解而致错
【例4】 在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=2BC,
A1B⊥B1C,求B1C与侧面A1ABB1所成角的余弦值.题型一题型二题型三题型四设BC=2,CC1=a(a>0),
则点A(4,0,0),A1(4,0,a),B(0,2,0),B1(0,2,a).题型一题型二题型三题型四错因分析错解中得到的只是直线B1C的方向向量与平面法向量的夹角,并非所求的线面角,应通过转化得到相应的结果.
2.能用向量方法解决线线、线面、面面夹角的问题.
3.了解向量方法在研究几何问题中的作用.【做一做1】 若异面直线l1的方向向量与l2的方向向量的夹角为150°,则l1与l2所成的角等于( )
A.30° B.150°
C.30°或150° D.以上均错
解析:由异面直线夹角定义知,异面直线夹角范围是(0°,90°].
答案:A【做一做2】 若直线l的方向向量与平面α的法向量的夹角等于120°,则直线l与平面α所成的角等于( )
A.120° B.60°
C.150° D.30°
解析:因为直线l的方向向量与平面α的法向量的夹角等于120°,所以它们所在直线的夹角为60°,则直线l与平面α所成的角等于90°-60°=30°.
答案:D
【做一做3】 若平面α的一个法向量为n1=(1,0,1),平面β的一个法向量是n2=(-3,1,3),则平面α与β所成的角等于( )
A.30° B.45° C.60° D.90°
解析:因为n1·n2=0,所以α⊥β,即平面α与β所成的角等于90°.
答案:D题型一题型二题型三题型四求异面直线所成的角
【例1】 在长方体ABCD-A1B1C1D1中,已知DA=DC=4,DD1=3,求异面直线A1B与B1C所成角的余弦值.题型一题型二题型三题型四反思建立空间直角坐标系,要充分利用题目中的垂直关系.利用向量法求两异面直线所成角的计算思路简便,但是要注意角的范围.题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四求直线与平面所成的角
【例2】 在棱长为1的正方体ABCD-A1B1C1D1中,在侧棱CC1上求一点P,使得直线AP与平面BDD1B1所成的角的正切值为3 .
解:如图,以D为坐标原点,分别以DA,DC,DD1所在直线为x轴、y轴、z轴建立空间直角坐标系.题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四【变式训练2】 在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD,PD=DC,E是PC的中点,求EB与平面ABCD夹角的余弦值.题型一题型二题型三题型四求二面角
【例3】 如图,四棱锥P-ABCD的底面ABCD是菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
(1)求证:AE⊥PD;
(2)若PA=AB=2,求二面角E-AF-C的余弦值.题型一题型二题型三题型四(1)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.
又BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE?平面ABCD,
所以PA⊥AE.
而PA?平面PAD,AD?平面PAD,且PA∩AD=A,所以AE⊥平面PAD.
又PD?平面PAD,所以AE⊥PD.题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四反思用几何法求二面角,往往需要作出其平面角,这是几何中的难点之一;而用向量法求解二面角无须作出二面角的平面角,只需求出平面的法向量,经过简单运算即可.题型一题型二题型三题型四【变式训练3】 如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;题型一题型二题型三题型四题型一题型二题型三题型四题型一题型二题型三题型四易错辨析
易错点 对向量法求线面角的原理不理解而致错
【例4】 在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=2BC,
A1B⊥B1C,求B1C与侧面A1ABB1所成角的余弦值.题型一题型二题型三题型四设BC=2,CC1=a(a>0),
则点A(4,0,0),A1(4,0,a),B(0,2,0),B1(0,2,a).题型一题型二题型三题型四错因分析错解中得到的只是直线B1C的方向向量与平面法向量的夹角,并非所求的线面角,应通过转化得到相应的结果.
