2019-2020学年高中数学新人教A版选修2-1课件:第三章空间向量与立体几何本章整合(50张)
文档属性
| 名称 | 2019-2020学年高中数学新人教A版选修2-1课件:第三章空间向量与立体几何本章整合(50张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-09-26 09:06:55 | ||
图片预览

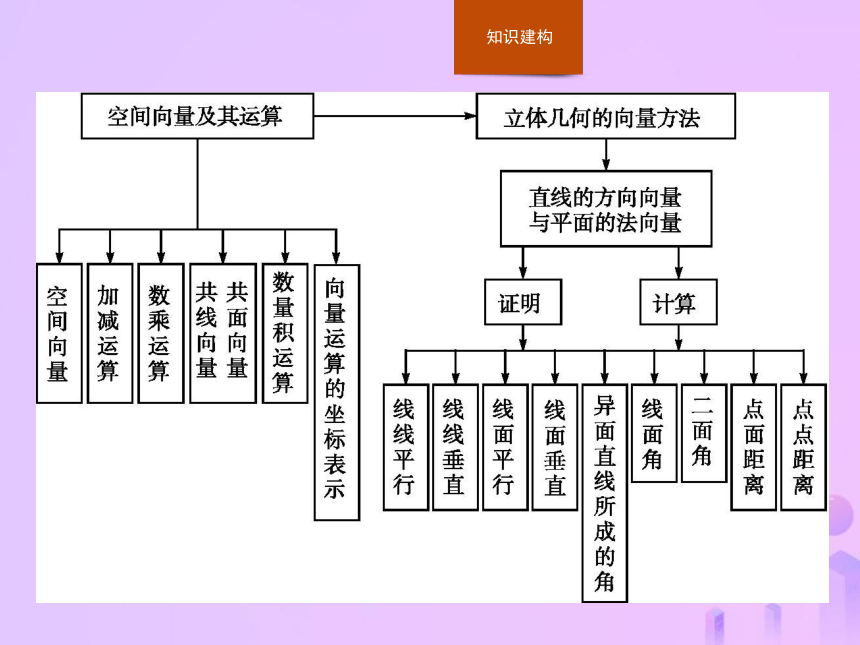










文档简介
课件50张PPT。本章整合专题一专题二专题三专题一 空间向量与线面的位置关系
用向量作为工具来研究几何,真正实现了几何中的形与代数中的数的有机结合.给立体几何的研究带来了极大的便利,不论是证明平行还是证明垂直,只需简单的运算就可以解决问题.专题一专题二专题三应用如图,在正方体ABCD-A1B1C1D1中,M,N分别为AB,B1C的中点.
(1)用向量法证明:平面A1BD∥平面B1CD1;
(2)用向量法证明:MN⊥平面A1BD.提示:(1)面面平行应转化为证明线面平行;(2)线面垂直应转化为线线垂直,最终结合面面平行与线面垂直的判定定理证明;此外本题也可建立空间直角坐标系转化为向量的坐标运算去求解.专题一专题二专题三解:(1)在正方体ABCD-A1B1C1D1中, 同理可证A1B∥D1C.
又BD∩A1B=B,B1D1∩D1C=D1,
故平面A1BD∥平面B1CD1.专题一专题二专题三又A1A⊥AD,A1A⊥AB,
∴c·b=0,c·a=0.
又|b|=|a|,∴b2=a2,∴b2-a2=0.专题一专题二专题三同理可证MN⊥A1B.又A1B∩BD=B,
∴MN⊥平面A1BD.
点评用向量法证明平行、垂直问题的步骤:
(1)建立空间图形与空间向量的关系(可以建立空间直角坐标系,也可以不建系),用空间向量表示问题中涉及的点、直线、平面;
(2)通过向量运算研究平行、垂直问题;
(3)根据运算结果解释相关问题.专题一专题二专题三专题二 空间向量与空间角
用几何法求异面直线所成的角、直线与平面所成的角、二面角时,都需要先作出(或证出)所求空间角的平面角,费时费力,难度较大.而利用向量法,只需求出直线的方向向量与平面的法向量即可求解,体现了向量法极大的优越性.专题一专题二专题三应用1如图所示的多面体是由三棱锥A-BDE与四棱锥D-BCFE拼接而成的,其中EF⊥平面AEB,AE⊥EB,AD∥EF∥BC,BC=2AD=4, EF=3,AE=BE=2,G是BC的中点.
(1)求异面直线BD与EG所成的角;
(2)求平面DEG与平面AEFD所成的钝二面角的正弦值.专题一专题二专题三解:(1)∵EF⊥平面AEB,AE?平面AEB,BE?平面AEB,
∴EF⊥AE,EF⊥BE.
又AE⊥EB,∴EB,EF,EA两两垂直.
以点E为坐标原点,EB,EF,EA分别为x,y,z轴建立如图所示的空间直角坐标系.
由已知,得点A(0,0,2),B(2,0,0),C(2,4,0),F(0,3,0),D(0,2,2),G(2,2,0),专题一专题二专题三专题一专题二专题三点评立体几何解答题的一般模式是首先证明线面位置关系(一般考虑使用综合几何方法进行证明),然后是与空间角有关的问题,综合几何方法和空间向量方法都可以,但使用综合几何方法要作出空间角的平面角,作图中要伴随着相关的证明,对空间想象能力与逻辑推理能力有较高的要求,而使用空间向量方法就是求直线的方向向量、平面的法向量,按照空间角的计算公式进行计算,也就是把几何问题完全代数化了,这种方法对运算能力有较高的要求.两种方法各有利弊,在解题中可根据情况灵活选用.专题一专题二专题三应用2在正方体ABCD-A1B1C1D1中,E,F分别为棱BB1和DD1的中点.
(1)求证:平面B1FC1∥平面ADE;
(2)试在棱DC上求一点M,使D1M⊥平面ADE;
(3)求二面角A1-DE-A的余弦值.专题一专题二专题三专题一专题二专题三专题一专题二专题三专题一专题二专题三专题三 利用空间向量解决探索性问题
立体几何探索性问题是近几年高考中的热点题型.空间向量作为一种工具,在解决立体几何探索性问题中有着无比的优越性,运用空间向量解立体几何问题,可使几何问题代数化,大大简化思维程序,使解题思路直观明了.
空间中的探索性问题一般有以下两种类型:
(1)“条件探索型”,就是指给出了问题的明确结论,但条件不足或未知,需要解题者探求、寻找使结论成立的条件的一类问题,这类问题的常用解法是逆推法,利用结论探求条件.
(2)“存在型”,是指结论不确定的问题,即在数学命题中,结论常以“是否存在”的形式出现,其结果可能存在,需要找出来;可能不存在,则需要说明理由.解答这一类问题时,先假设结论存在,若推证无矛盾,则结论存在;若推证出矛盾,则结论不存在.专题一专题二专题三应用1如图,已知在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5, AA1=4.
(1)求证:AC⊥BC1;
(2)在AB上是否存在点D,使得AC1⊥CD?
(3)在AB上是否存在点E,使得AC1∥平面CEB1?专题一专题二专题三解:(1)在直三棱柱ABC-A1B1C1中,因为AC=3,BC=4,AB=5,所以AC2+BC2=AB2,即AC⊥BC,所以AC,BC,CC1两两垂直,以C为原点,直线CA,CB,CC1分别为x轴、y轴、z轴建立如图空间直角坐标系.
则点C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4).所以-9+9λ=0,解得λ=1.
所以在AB上存在点D使得AC1⊥CD,此时点D与点B重合.专题一专题二专题三所以在AB上存在点E,使得AC1∥平面CEB1,此时点E为AB的中点.专题一专题二专题三专题一专题二专题三解:建立如图所示的空间直角坐标系,不妨设AB=1,则点B(1,0,0),C(1,1,0),D(0,3,0),F(0,0,1),E(0,1,1).专题一专题二专题三(2)设平面CDE的法向量为n=(x,y,z), 专题一专题二专题三123456789解析:以DA,DC,DD1为轴建立空间直角坐标系如图, 答案:C 123456789123456789解析:如图,取AB的中点F,连接EF. 答案:A 1234567893(2018全国1高考)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值.123456789解:(1)由已知可得,BF⊥PF,BF⊥EF,
所以BF⊥平面PEF.
又BF?平面ABFD,所以平面PEF⊥平面ABFD.
(2)作PH⊥EF,垂足为H.
由(1)得,PH⊥平面ABFD.123456789123456789(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.123456789解:(1)因为AP=CP=AC=4,O为AC的中点, ?123456789设平面PAM的法向量为n=(x,y,z). 1234567895(2018全国3高考)如图,边长为2的正方形ABCD所在的平面与半 (1)证明:平面AMD⊥平面BMC;
(2)当三棱锥M-ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.
解:(1)由题设知,平面CMD⊥平面ABCD,交线为CD.
因为BC⊥CD,BC?平面ABCD,
所以BC⊥平面CMD,故BC⊥DM.所以DM⊥CM.
又BC∩CM=C,所以DM⊥平面BMC.
而DM?平面AMD,故平面AMD⊥平面BMC.1234567891234567896(2018天津高考)如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2.
(1)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;
(2)求二面角E-BC-F的正弦值;
(3)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.1234567891234567891234567891234567897(2017全国1高考)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.
解:(1)由已知∠BAP=∠CDP=90°,
得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,从而AB⊥平面PAD.
又AB?平面PAB,所以平面PAB⊥平面PAD.123456789(2)在平面PAD内作PF⊥AD,垂足为F.
由(1)可知,AB⊥平面PAD,
故AB⊥PF,可得PF⊥平面ABCD.1234567891234567898(2017全国2高考)如图,四棱锥P-ABCD中,侧面PAD为等边三角 PD的中点.
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.123456789解:(1)取PA的中点F,连接EF,BF. 又BF?平面PAB,CE?平面PAB,
故CE∥平面PAB.1234567891234567891234567899(2017全国3高考)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D-AE-C的余弦值.123456789解:(1)由题设可得,△ABD≌△CBD,从而AD=DC.
又△ACD是直角三角形,所以∠ADC=90°.
取AC的中点O,连接DO,BO,
则DO⊥AC,DO=AO.
又由于△ABC是正三角形,故BO⊥AC.
所以∠DOB为二面角D-AC-B的平面角.
在Rt△AOB中,BO2+AO2=AB2,
又AB=BD,
所以BO2+DO2=BO2+AO2=AB2=BD2,
故∠DOB=90°.
所以平面ACD⊥平面ABC.123456789123456789
用向量作为工具来研究几何,真正实现了几何中的形与代数中的数的有机结合.给立体几何的研究带来了极大的便利,不论是证明平行还是证明垂直,只需简单的运算就可以解决问题.专题一专题二专题三应用如图,在正方体ABCD-A1B1C1D1中,M,N分别为AB,B1C的中点.
(1)用向量法证明:平面A1BD∥平面B1CD1;
(2)用向量法证明:MN⊥平面A1BD.提示:(1)面面平行应转化为证明线面平行;(2)线面垂直应转化为线线垂直,最终结合面面平行与线面垂直的判定定理证明;此外本题也可建立空间直角坐标系转化为向量的坐标运算去求解.专题一专题二专题三解:(1)在正方体ABCD-A1B1C1D1中, 同理可证A1B∥D1C.
又BD∩A1B=B,B1D1∩D1C=D1,
故平面A1BD∥平面B1CD1.专题一专题二专题三又A1A⊥AD,A1A⊥AB,
∴c·b=0,c·a=0.
又|b|=|a|,∴b2=a2,∴b2-a2=0.专题一专题二专题三同理可证MN⊥A1B.又A1B∩BD=B,
∴MN⊥平面A1BD.
点评用向量法证明平行、垂直问题的步骤:
(1)建立空间图形与空间向量的关系(可以建立空间直角坐标系,也可以不建系),用空间向量表示问题中涉及的点、直线、平面;
(2)通过向量运算研究平行、垂直问题;
(3)根据运算结果解释相关问题.专题一专题二专题三专题二 空间向量与空间角
用几何法求异面直线所成的角、直线与平面所成的角、二面角时,都需要先作出(或证出)所求空间角的平面角,费时费力,难度较大.而利用向量法,只需求出直线的方向向量与平面的法向量即可求解,体现了向量法极大的优越性.专题一专题二专题三应用1如图所示的多面体是由三棱锥A-BDE与四棱锥D-BCFE拼接而成的,其中EF⊥平面AEB,AE⊥EB,AD∥EF∥BC,BC=2AD=4, EF=3,AE=BE=2,G是BC的中点.
(1)求异面直线BD与EG所成的角;
(2)求平面DEG与平面AEFD所成的钝二面角的正弦值.专题一专题二专题三解:(1)∵EF⊥平面AEB,AE?平面AEB,BE?平面AEB,
∴EF⊥AE,EF⊥BE.
又AE⊥EB,∴EB,EF,EA两两垂直.
以点E为坐标原点,EB,EF,EA分别为x,y,z轴建立如图所示的空间直角坐标系.
由已知,得点A(0,0,2),B(2,0,0),C(2,4,0),F(0,3,0),D(0,2,2),G(2,2,0),专题一专题二专题三专题一专题二专题三点评立体几何解答题的一般模式是首先证明线面位置关系(一般考虑使用综合几何方法进行证明),然后是与空间角有关的问题,综合几何方法和空间向量方法都可以,但使用综合几何方法要作出空间角的平面角,作图中要伴随着相关的证明,对空间想象能力与逻辑推理能力有较高的要求,而使用空间向量方法就是求直线的方向向量、平面的法向量,按照空间角的计算公式进行计算,也就是把几何问题完全代数化了,这种方法对运算能力有较高的要求.两种方法各有利弊,在解题中可根据情况灵活选用.专题一专题二专题三应用2在正方体ABCD-A1B1C1D1中,E,F分别为棱BB1和DD1的中点.
(1)求证:平面B1FC1∥平面ADE;
(2)试在棱DC上求一点M,使D1M⊥平面ADE;
(3)求二面角A1-DE-A的余弦值.专题一专题二专题三专题一专题二专题三专题一专题二专题三专题一专题二专题三专题三 利用空间向量解决探索性问题
立体几何探索性问题是近几年高考中的热点题型.空间向量作为一种工具,在解决立体几何探索性问题中有着无比的优越性,运用空间向量解立体几何问题,可使几何问题代数化,大大简化思维程序,使解题思路直观明了.
空间中的探索性问题一般有以下两种类型:
(1)“条件探索型”,就是指给出了问题的明确结论,但条件不足或未知,需要解题者探求、寻找使结论成立的条件的一类问题,这类问题的常用解法是逆推法,利用结论探求条件.
(2)“存在型”,是指结论不确定的问题,即在数学命题中,结论常以“是否存在”的形式出现,其结果可能存在,需要找出来;可能不存在,则需要说明理由.解答这一类问题时,先假设结论存在,若推证无矛盾,则结论存在;若推证出矛盾,则结论不存在.专题一专题二专题三应用1如图,已知在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5, AA1=4.
(1)求证:AC⊥BC1;
(2)在AB上是否存在点D,使得AC1⊥CD?
(3)在AB上是否存在点E,使得AC1∥平面CEB1?专题一专题二专题三解:(1)在直三棱柱ABC-A1B1C1中,因为AC=3,BC=4,AB=5,所以AC2+BC2=AB2,即AC⊥BC,所以AC,BC,CC1两两垂直,以C为原点,直线CA,CB,CC1分别为x轴、y轴、z轴建立如图空间直角坐标系.
则点C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4).所以-9+9λ=0,解得λ=1.
所以在AB上存在点D使得AC1⊥CD,此时点D与点B重合.专题一专题二专题三所以在AB上存在点E,使得AC1∥平面CEB1,此时点E为AB的中点.专题一专题二专题三专题一专题二专题三解:建立如图所示的空间直角坐标系,不妨设AB=1,则点B(1,0,0),C(1,1,0),D(0,3,0),F(0,0,1),E(0,1,1).专题一专题二专题三(2)设平面CDE的法向量为n=(x,y,z), 专题一专题二专题三123456789解析:以DA,DC,DD1为轴建立空间直角坐标系如图, 答案:C 123456789123456789解析:如图,取AB的中点F,连接EF. 答案:A 1234567893(2018全国1高考)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值.123456789解:(1)由已知可得,BF⊥PF,BF⊥EF,
所以BF⊥平面PEF.
又BF?平面ABFD,所以平面PEF⊥平面ABFD.
(2)作PH⊥EF,垂足为H.
由(1)得,PH⊥平面ABFD.123456789123456789(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且二面角M-PA-C为30°,求PC与平面PAM所成角的正弦值.123456789解:(1)因为AP=CP=AC=4,O为AC的中点, ?123456789设平面PAM的法向量为n=(x,y,z). 1234567895(2018全国3高考)如图,边长为2的正方形ABCD所在的平面与半 (1)证明:平面AMD⊥平面BMC;
(2)当三棱锥M-ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.
解:(1)由题设知,平面CMD⊥平面ABCD,交线为CD.
因为BC⊥CD,BC?平面ABCD,
所以BC⊥平面CMD,故BC⊥DM.所以DM⊥CM.
又BC∩CM=C,所以DM⊥平面BMC.
而DM?平面AMD,故平面AMD⊥平面BMC.1234567891234567896(2018天津高考)如图,AD∥BC且AD=2BC,AD⊥CD,EG∥AD且EG=AD,CD∥FG且CD=2FG,DG⊥平面ABCD,DA=DC=DG=2.
(1)若M为CF的中点,N为EG的中点,求证:MN∥平面CDE;
(2)求二面角E-BC-F的正弦值;
(3)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.1234567891234567891234567891234567897(2017全国1高考)如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,求二面角A-PB-C的余弦值.
解:(1)由已知∠BAP=∠CDP=90°,
得AB⊥AP,CD⊥PD.
由于AB∥CD,故AB⊥PD,从而AB⊥平面PAD.
又AB?平面PAB,所以平面PAB⊥平面PAD.123456789(2)在平面PAD内作PF⊥AD,垂足为F.
由(1)可知,AB⊥平面PAD,
故AB⊥PF,可得PF⊥平面ABCD.1234567891234567898(2017全国2高考)如图,四棱锥P-ABCD中,侧面PAD为等边三角 PD的中点.
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.123456789解:(1)取PA的中点F,连接EF,BF. 又BF?平面PAB,CE?平面PAB,
故CE∥平面PAB.1234567891234567891234567899(2017全国3高考)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(1)证明:平面ACD⊥平面ABC;
(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D-AE-C的余弦值.123456789解:(1)由题设可得,△ABD≌△CBD,从而AD=DC.
又△ACD是直角三角形,所以∠ADC=90°.
取AC的中点O,连接DO,BO,
则DO⊥AC,DO=AO.
又由于△ABC是正三角形,故BO⊥AC.
所以∠DOB为二面角D-AC-B的平面角.
在Rt△AOB中,BO2+AO2=AB2,
又AB=BD,
所以BO2+DO2=BO2+AO2=AB2=BD2,
故∠DOB=90°.
所以平面ACD⊥平面ABC.123456789123456789
